Co wyjaśnia wariancja? (definicja – przykład)

Wyjaśniona wariancja (czasami nazywana „wyjaśnioną zmiennością”) odnosi się do wariancji zmiennej odpowiedzi w modelu, którą można wyjaśnić za pomocą zmiennych predykcyjnych modelu.

Im wyższa wyjaśniona wariancja modelu, tym większą zmienność danych model jest w stanie wyjaśnić.

Wyjaśniona wariancja pojawia się w wynikach dwóch różnych modeli statystycznych:

1. ANOVA: stosowana do porównania średnich z trzech lub więcej niezależnych grup.

2. Regresja: stosowana do ilościowego określenia związku pomiędzy jedną lub większą liczbą zmiennych predykcyjnych a zmienną odpowiedzi.

Poniższe przykłady pokazują, jak interpretować wariancję resztową w każdej z tych metod.

Uwaga : Przeciwieństwo wyjaśnionej wariancji nazywa się wariancją resztową .

Wariancja wyjaśniona w modelach ANOVA

Za każdym razem, gdy dopasowujemy model ANOVA („analiza wariancji”), otrzymujemy tabelę ANOVA, która wygląda następująco:

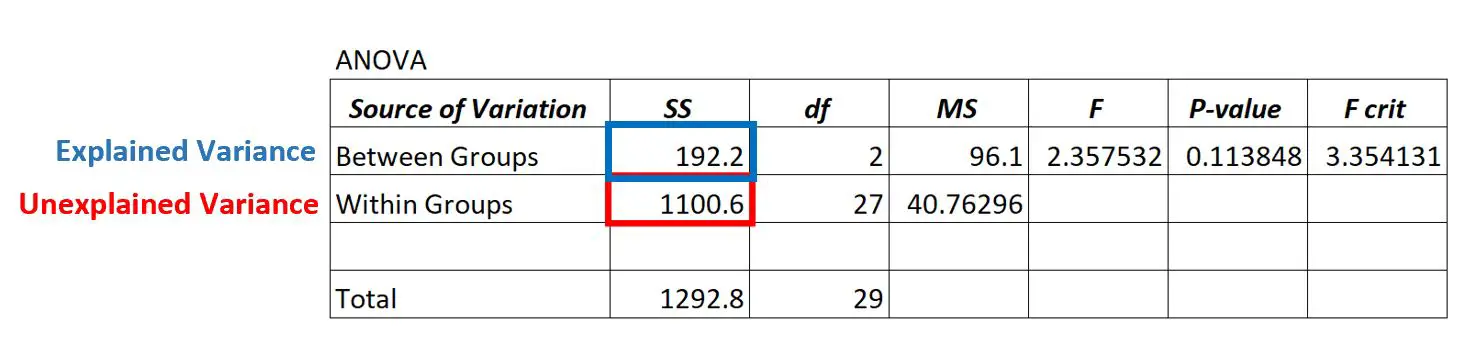
Wyjaśnioną wariancję można znaleźć w kolumnie SS („suma kwadratów”) dla zmienności międzygrupowej .

W powyższym modelu ANOVA widzimy, że wyjaśniona wariancja wynosi 192,2.

Aby określić, czy wyjaśniona wariancja jest „wysoka”, możemy obliczyć średnią sumę kwadratów dla grup i średnią sumę kwadratów pomiędzy grupami i znaleźć stosunek między nimi, co daje ogólną wartość F w tabeli ANOVA.

• F = MS _wchodzi / MS _wchodzi
• F = 96,1 / 40,76296
• F = 2,357

Wartość F w powyższej tabeli ANOVA wynosi 2,357, a odpowiadająca jej wartość p wynosi 0,113848.

Ponieważ ta wartość p jest nie mniejsza niż α = 0,05, nie mamy wystarczających dowodów, aby odrzucić hipotezę zerową ANOVA .

Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że średnia różnica między porównywanymi grupami jest znacząco różna.

Mówi nam to, że wyjaśniona wariancja w modelu ANOVA jest niewielka w porównaniu z niewyjaśnioną wariancją.

Wariancja wyjaśniona w modelach regresji

W modelu regresji wyjaśnioną wariancję podsumowuje się jako R-kwadrat , często zapisywany jako ^R2 .

Wartość ta reprezentuje proporcję wariancji zmiennej odpowiedzi, którą można wyjaśnić za pomocą zmiennych predykcyjnych w modelu.

Wartość R do kwadratu może wynosić od 0 do gdzie:

• Wartość 0 wskazuje, że zmiennej odpowiedzi nie można w ogóle wyjaśnić za pomocą zmiennych predykcyjnych.
• Wartość 1 wskazuje, że zmienną odpowiedzi można doskonale i bezbłędnie wyjaśnić za pomocą zmiennych predykcyjnych.

Kiedy dopasowujemy model regresji, zwykle otrzymujemy wynik wyglądający następująco:

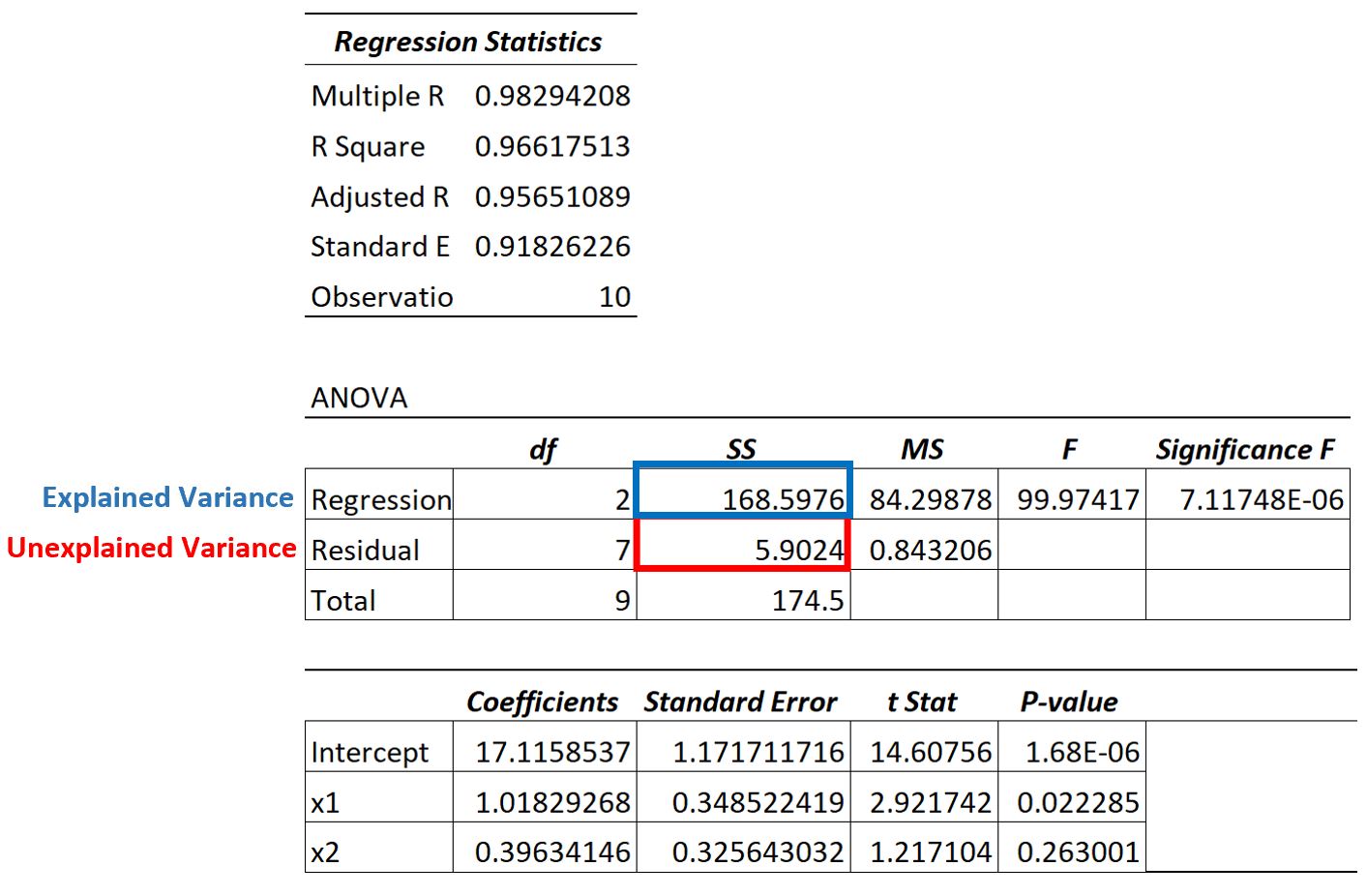
Widzimy, że wyjaśniona wariancja wynosi 168,5976 , a całkowita wariancja wynosi 174,5 .

Korzystając z tych wartości, możemy obliczyć wartość R-kwadrat dla tego modelu regresji w następujący sposób:

• R kwadrat: Regresja SS / Suma SS
• R do kwadratu: 168,5976 / 174,5
• R do kwadratu: 0,966

Ponieważ wartość R-kwadrat tego modelu jest bliska 1, mówi nam to, że wariancja wyjaśniona w modelu jest niezwykle duża.

Innymi słowy, model jest w stanie dobrze wykorzystać zmienne predykcyjne do wyjaśnienia zmienności zmiennej odpowiedzi.

Powiązane: Jaka jest dobra wartość R-kwadrat?