Macierz kowariancji

W tym artykule wyjaśniono, czym jest macierz kowariancji i jaki jest jej wzór. Dowiesz się, jak utworzyć macierz kowariancji na konkretnym przykładzie i właściwości macierzy kowariancji.

Co to jest macierz kowariancji?

Macierz kowariancji jest macierzą kwadratową, której elementami są wariancje i kowariancje badanych zmiennych. Zatem elementy głównej przekątnej macierzy kowariancji są wariancją każdej zmiennej, a pozostałe elementy są kowariancjami między zmiennymi.

W statystyce macierz kowariancji służy do analizy związku między dwiema lub większą liczbą zmiennych losowych. Macierz kowariancji jest bardzo przydatna, ponieważ pozwala szybko zinterpretować korelację między wieloma zmiennymi, ponieważ można zobaczyć wartości wszystkich kowariancji zmiennych jednocześnie.

Symbolem macierzy kowariancji jest wielka grecka litera sigma (Σ).

Jak obliczyć macierz kowariancji

Aby obliczyć macierz kowariancji kilku zmiennych statystycznych, należy wykonać następujące kroki:

1. Oblicz wariancje wszystkich zmiennych.
2. Oblicz kowariancję każdej pary zmiennych.
3. Utwórz macierz kowariancji:
• Wariancję zmiennej i należy umieścić na głównej przekątnej macierzy, a dokładniej w pozycji i,i .
• Kowariancję pomiędzy zmiennymi i oraz j należy umieścić na pozycji i,j macierzy.

Wzór na macierz kowariancji jest zatem następujący:

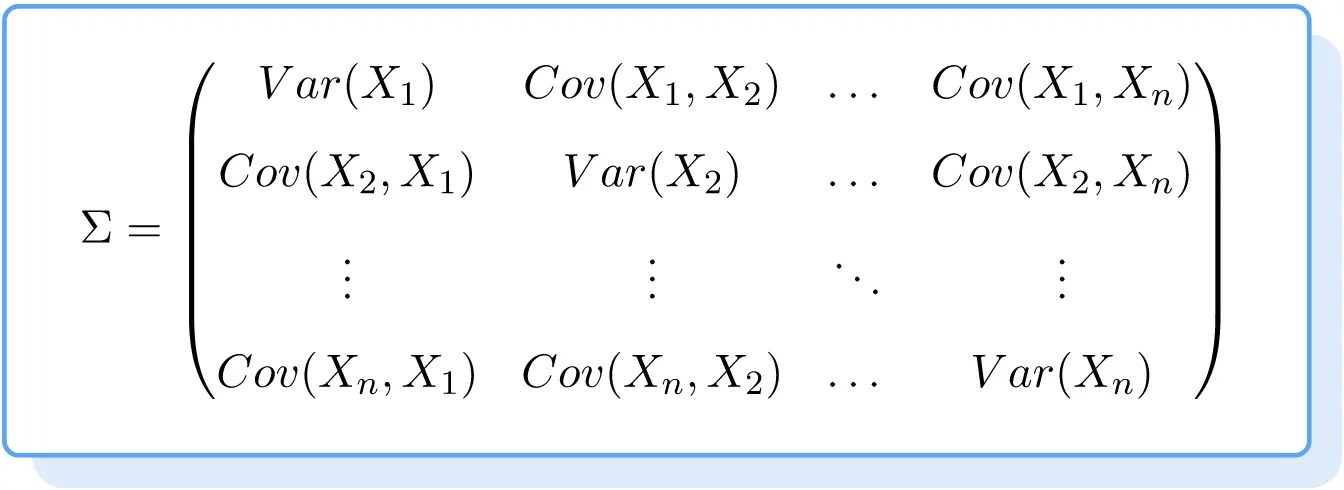
Przykład macierzy kowariancji

Po zapoznaniu się z definicją macierzy kowariancji poniżej znajduje się ćwiczenie krok po kroku, dzięki któremu można zobaczyć, jak powstaje tego typu macierz.

Oblicza macierz kowariancji zmiennych X, Y i Z, których wartości wynoszą:

• X: 4, 7, 12, 5, 7
• Oraz: 9, 15, 19, 6, 8
• Z: 7, 2, 4, 6, 3

Pierwszą rzeczą, którą musimy zrobić, to określić wariancje wszystkich zmiennych:

Po drugie, znajdujemy kowariancję pomiędzy każdą parą zmiennych:

Kiedy już obliczyliśmy wszystkie wariancje i kowariancje, pozostaje nam tylko sporządzić macierz kowariancji. Aby to zrobić, umieszczamy wartości wariancji na głównej przekątnej macierzy, a wartości kowariancji w odpowiednich pozycjach:

Jak widać, przedstawiając wariancje i kowariancje w macierzy, bardzo łatwo jest zinterpretować zmienne. Zmienną o największym rozproszeniu jest Y (23,44), natomiast zmienne X i Y mają bezpośredni związek, natomiast zmienne X i Z (a więc Y i Z) mają odwrotną zależność.

Należy zauważyć, że macierz kowariancji jest zawsze symetryczna, ponieważ kowariancja między dwiema zmiennymi nie zależy od kolejności zmiennych. Na przykład,

jest równe

Dodatkowo macierz kowariancji będzie zawsze macierzą kwadratową, a jej wymiar będzie równy liczbie zmiennych. W tym przypadku mieliśmy trzy zmienne i dlatego jest to macierz 3×3, ale gdybyśmy mieli tylko dwie zmienne, macierz kowariancji wyniosłaby 2×2.

Własności macierzy kowariancji

Macierz kowariancji ma następujące cechy:

• Macierz kowariancji jest macierzą kwadratową rzędu liczby zmiennych.
• Macierz kowariancji jest symetryczna, co oznacza, że główna przekątna macierzy jest osią symetrii.
• Macierz kowariancji jest zawsze dodatnia półokreślona.
• Wyznacznik macierzy kowariancji jest równy lub większy od zera.