Macierz korelacji

W tym artykule dowiesz się, czym jest macierz korelacji, jaki jest jej wzór i jak interpretować macierz korelacji. Dodatkowo będzie można zobaczyć konkretny przykład interpretacji macierzy korelacji.

Co to jest macierz korelacji?

Macierz korelacji jest macierzą, która zawiera w pozycji i,j współczynnik korelacji pomiędzy zmiennymi i oraz j .

Zatem macierz korelacji jest macierzą kwadratową wypełnioną jedynkami na głównej przekątnej, a elementem wiersza i kolumny j jest wartość współczynnika korelacji pomiędzy zmienną i a zmienną j .

Wzór na macierz korelacji jest zatem następujący:

Złoto

jest współczynnikiem korelacji pomiędzy zmiennymi

I

Zatem, aby znaleźć macierz korelacji zbioru danych, niezbędna jest wiedza, w jaki sposób obliczany jest współczynnik korelacji. Jeśli nie pamiętasz, pod poniższym linkiem dowiesz się, jak to zrobić za pomocą kalkulatora online:

Właściwością współczynnika korelacji jest to, że przy jego obliczaniu kolejność zmiennych nie ma znaczenia, czyli współczynnik korelacji

jest równa

Dlatego macierz korelacji jest symetryczna.

Aby macierz korelacji była miarodajna, zbiór danych statystycznych musi zawierać więcej niż dwie zmienne. W przeciwnym razie wystarczyłoby wyznaczyć pojedynczy współczynnik korelacji i macierz korelacji byłaby miarodajna.

Jak zrobić macierz korelacji

Mając na uwadze definicję macierzy korelacji, przyjrzyjmy się, jak powstaje tego typu macierz statystyczna:

1. Oblicz współczynnik korelacji każdej pary zmiennych. Należy pamiętać, że kolejność zmiennych nie zmienia wyniku, dlatego należy ją obliczyć tylko raz dla każdej pary zmiennych.
2. Utwórz macierz kwadratową o tym samym wymiarze, co liczba zmiennych w serii danych. Ta macierz będzie macierzą korelacji.
3. Wpisz 1 w każdym elemencie głównej przekątnej macierzy korelacji.
4. Umieść współczynnik korelacji zmiennych i , j na pozycjach i , j oraz j , i .
5. Po utworzeniu macierzy korelacji pozostaje jedynie zinterpretować jej wartości.

Należy pamiętać, że samo uruchomienie macierzy korelacji nie wystarczy, należy wówczas zinterpretować jej wartości i zrozumieć, co one oznaczają. W poniższej sekcji wyjaśniono, jak interpretować macierz korelacji.

Interpretacja macierzy korelacji

Aby poprawnie zinterpretować macierz korelacji należy wziąć pod uwagę, że wartość współczynnika korelacji może wynosić od -1 do +1:

• r=-1 : obie zmienne mają idealną ujemną korelację, więc możemy narysować linię o nachyleniu ujemnym, w której wszystkie punkty się łączą.
• -1<r<0 : korelacja między dwiema zmiennymi jest ujemna, więc gdy jedna zmienna rośnie, druga maleje. Im wartość jest bliższa -1, tym bardziej ujemnie powiązane są zmienne.
• r=0 : korelacja między dwiema zmiennymi jest bardzo słaba, w rzeczywistości zależność liniowa między nimi wynosi zero. Nie oznacza to, że zmienne są niezależne, ponieważ mogą mieć zależność nieliniową.
• 0<r<1 : korelacja między dwiema zmiennymi jest dodatnia, im wartość jest bliższa +1, tym silniejszy jest związek między zmiennymi. W tym przypadku jedna zmienna ma tendencję do zwiększania swojej wartości, podczas gdy druga również rośnie.
• r=1 : obie zmienne mają doskonałą dodatnią korelację, to znaczy mają dodatnią zależność liniową.

Zatem, aby zinterpretować macierz korelacji, należy zinterpretować każdy współczynnik korelacji i porównać różne wyniki.

W ten sposób będziesz mógł zobaczyć, które zmienne są ze sobą najbardziej powiązane, które zmienne są najważniejsze, które zmienne praktycznie nie mają ze sobą żadnego związku itp.

Przykład macierzy korelacji

Aby w pełni zrozumieć, z czego składa się macierz korelacji i jak ją interpretować, w tej sekcji przeanalizujemy przykładową macierz korelacji:

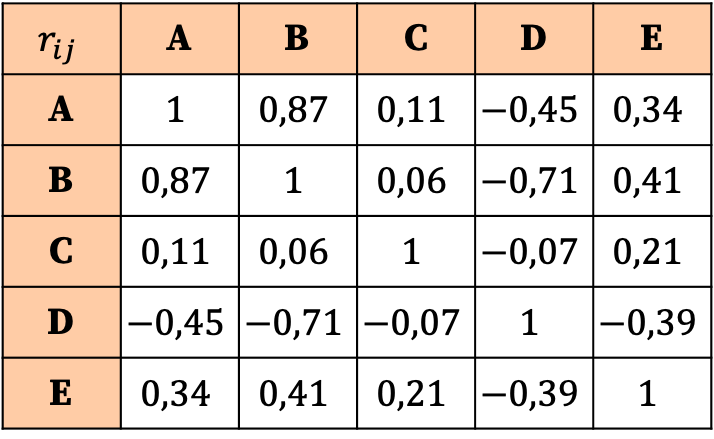
Interpretacja macierzy korelacji opiera się na wartościach współczynników. Widzimy więc, że najsilniejszą korelacją jest relacja między zmienną A i zmienną B, gdyż odpowiadający jej współczynnik jest największy (0,87).

Natomiast zmienna C praktycznie nie ma korelacji z żadną zmienną, gdyż wszystkie jej współczynniki są bardzo bliskie zeru, a zatem bardzo niskie. Zatem dla uproszczenia analizy można by nawet rozważyć usunięcie tej zmiennej z badania statystycznego.

Podobnie wszystkie relacje zmiennej D z innymi zmiennymi są ujemne, co oznacza, że korelacja między zmienną D a innymi zmiennymi jest odwrotna. Nie oznacza to, że zmienną należy wyeliminować, a jedynie, że zmienna D jest ujemnie skorelowana.

Jak widać, macierz korelacji jest bardzo przydatna do podsumowania danych i dokonania ogólnej analizy relacji pomiędzy różnymi zmiennymi w zbiorze danych.