Jak utworzyć macierz korelacji w sas-ie (z przykładem)
Macierz korelacji to kwadratowa tabela pokazująca współczynniki korelacji pomiędzy zmiennymi w zbiorze danych.
Zapewnia szybki sposób zrozumienia siły zależności liniowych istniejących między zmiennymi w zbiorze danych.
Za pomocą instrukcji PROC CORR w SAS-ie możesz utworzyć macierz korelacji dla danego zbioru danych:
/*create correlation matrix using all numeric variables in my_data*/
proc corr data =my_data;
run ;
Domyślnie spowoduje to utworzenie macierzy wyświetlającej współczynniki korelacji pomiędzy wszystkimi zmiennymi numerycznymi w zbiorze danych.
Aby uwzględnić w macierzy korelacji tylko określone zmienne, można skorzystać z instrukcji VAR :
/*create correlation matrix using only var1, var2 and var3 in my_data*/
proc corr data =my_data;
var var1, var2, var3;
run ;
Poniższy przykład pokazuje, jak utworzyć macierz korelacji w SAS-ie.
Przykład: Tworzenie macierzy korelacji w SAS-ie
Załóżmy, że mamy następujący zbiór danych w SAS-ie, który zawiera informacje o różnych koszykarzach:
/*create dataset*/
data my_data;
input team $ assists rebounds points;
datalines ;
A 4 12 22
A 5 14 24
A 5 13 26
A 6 7 26
B 7 8 29
B 8 8 32
B 8 9 20
B 10 13 14
;
run ;
/*view dataset*/
proc print data =my_data;
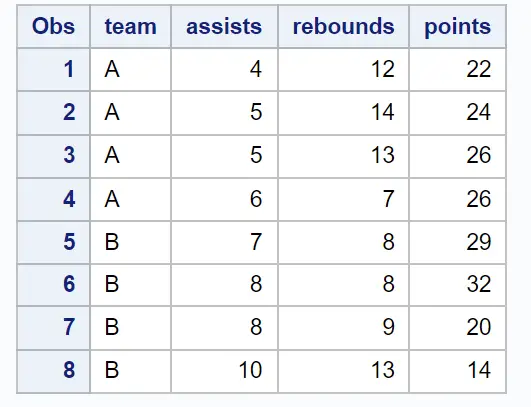
Możemy użyć instrukcji PROC CORR, aby utworzyć macierz korelacji, która domyślnie zawiera każdą zmienną numeryczną w zbiorze danych:
/*create correlation matrix using all numeric variables in my_data*/
proc corr data =my_data;
run ;
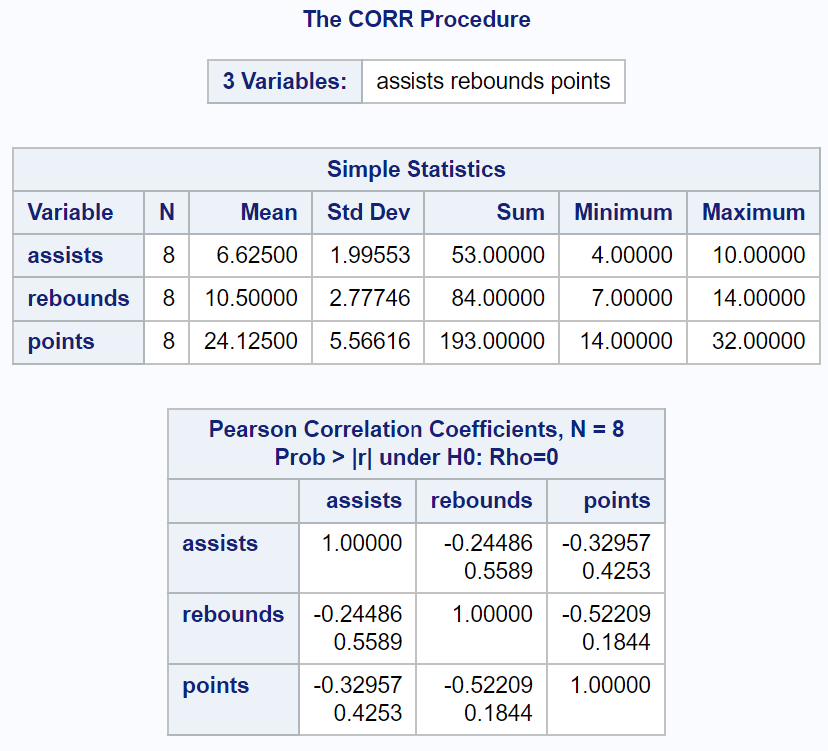
Dane wyjściowe wyświetlają statystyki podsumowujące zmiennych numerycznych w pierwszej tabeli wraz z macierzą korelacji.
Należy zauważyć, że zmienna „zespół” nie została uwzględniona w macierzy korelacji, ponieważ nie była zmienną liczbową.
Oto jak interpretować wartości macierzy korelacji:
(1) Współczynnik korelacji Pearsona (r) pomiędzy asystami i zbiórkami wynosi -0,24486 . Odpowiednia wartość p wynosi 0,5589 .
Ponieważ r jest mniejsze od zera, mówi nam to, że pomiędzy tymi dwiema zmiennymi istnieje ujemna zależność liniowa. Jednakże wartość p jest nie mniejsza niż 0,05, więc korelacja ta nie jest istotna statystycznie.
(2) Współczynnik korelacji Pearsona (r) pomiędzy asystami i punktami wynosi -0,32957 . Odpowiednia wartość p wynosi 0,4253 .
Istnieje negatywna zależność liniowa pomiędzy tymi dwiema zmiennymi, ale nie jest ona istotna statystycznie.
(3) Współczynnik korelacji Pearsona (r) pomiędzy zbiórkami i punktami wynosi -0,52209 . Odpowiednia wartość p wynosi 0,1844 .
Istnieje negatywna zależność liniowa pomiędzy tymi dwiema zmiennymi, ale nie jest ona istotna statystycznie.
Należy zauważyć, że możemy również użyć instrukcji VAR , aby uwzględnić w macierzy korelacji tylko określone zmienne numeryczne:
/*create correlation matrix using only assists and rebounds variables*/
proc corr data =my_data;
var assists rebounds;
run ;

Należy zauważyć, że w tej macierzy korelacji uwzględniono jedynie zmienne asyst i zbiórek .
Dodatkowe zasoby
Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w SAS-ie:
Jak utworzyć macierz wykresu rozrzutu w SAS-ie
Jak tworzyć tabele przestawne w SAS-ie
Jak obliczyć współczynnik inflacji wariancji (VIF) w SAS