Jak znaleźć medianę zgrupowanych danych: z przykładami

Często chcemy obliczyć medianę danych zgrupowanych w jakiś sposób.

Przypomnijmy, że mediana reprezentuje wartość znajdującą się bezpośrednio w środku zbioru danych, gdy wszystkie wartości są uporządkowane od najmniejszej do największej.

Załóżmy na przykład, że mamy następujące pogrupowane dane:

Chociaż nie jest możliwe obliczenie dokładnej mediany, ponieważ nie znamy wartości danych surowych , możliwe jest oszacowanie mediany za pomocą następującego wzoru:

Mediana zgrupowanych danych = L + W[(N/2 – C) / F]

Złoto:

• L : Dolna granica klasy mediany
• W : Mediana szerokości klasy
• N : Częstotliwość całkowita
• C : Częstotliwość skumulowana do klasy mediany
• F : Mediana częstotliwości klas

Uwaga : Klasa średnia to klasa, która zawiera wartość znajdującą się w N/2. W powyższym przykładzie jest N = 23 wartości ogółem. Zatem wartość mediany jest taka, że na pozycji 23/2 = 11,5, czyli w klasie 21-30.

Poniższe przykłady pokazują, jak obliczyć medianę pogrupowanych danych w różnych scenariuszach.

Przykład 1: Oblicz medianę zgrupowanych danych

Załóżmy, że mamy następujący rozkład częstotliwości, który pokazuje egzamin oceniony przez 40 uczniów w określonej klasie:

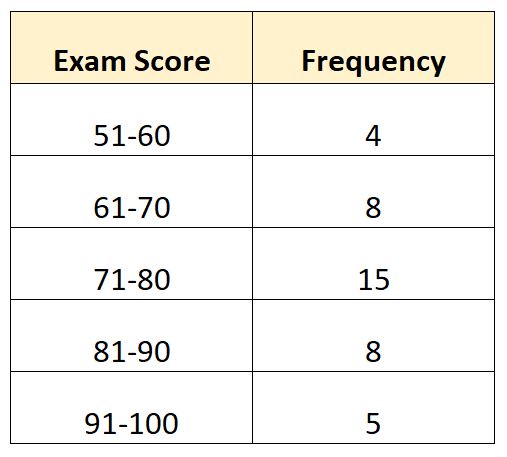
W tym przykładzie jest N = 40 wartości całkowitych. Zatem wartość mediana należy do klasy, w której znajduje się 40/2 = 20. Dwudziesta największa wartość będzie należeć do klasy 71-80 .

Wiedząc o tym, możemy obliczyć następujące wartości:

• L : Dolna granica klasy średniej: 71
• W : Mediana szerokości klasy: 9
• N : Całkowita częstotliwość: 40
• C : Częstotliwość skumulowana do klasy mediany: 12
• F : Mediana częstotliwości zajęć: 15

Możemy te wartości wstawić do wzoru, aby obliczyć medianę rozkładu:

• Mediana = L + W[(N/2 – C) / F]
• Mediana = 71 + 9[(40/2 – 12) / 15]
• Mediana = 75,8

Szacujemy, że średni wynik egzaminu wynosi 75,8 .

Przykład 2: Oblicz medianę zgrupowanych danych

Załóżmy, że mamy następujący rozkład częstotliwości, który pokazuje liczbę punktów zdobytych na mecz przez 60 koszykarzy:

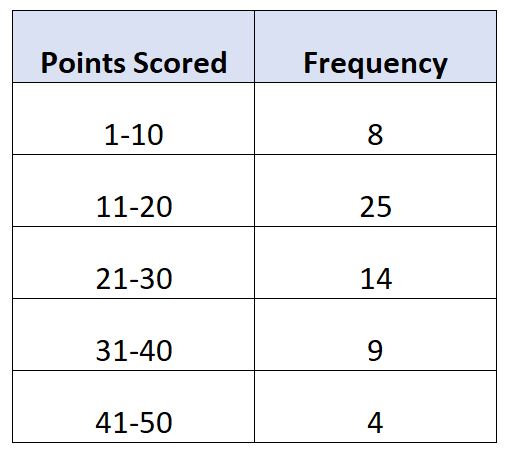
W tym przykładzie jest N = 60 wartości całkowitych. Zatem wartość mediany należy do klasy, w której mieści się 60/2 = 30. 30. największa wartość będzie w klasie 11-20 .

Wiedząc o tym, możemy obliczyć następujące wartości:

• L : Dolna granica klasy średniej: 11
• W : Mediana szerokości klasy: 9
• N : Całkowita częstotliwość: 60
• C : Częstotliwość skumulowana do klasy mediany: 8
• F : Mediana częstotliwości zajęć: 25

Możemy te wartości wstawić do wzoru, aby obliczyć medianę rozkładu:

• Mediana = L + W[(N/2 – C) / F]
• Mediana = 11 + 9[(60/2 – 8) / 25]
• Mediana = 18,92

Szacujemy, że średni wynik egzaminu wynosi 18,92 .

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe operacje na zgrupowanych danych:

Jak znaleźć średnią i odchylenie standardowe pogrupowanych danych
Jak znaleźć tryb pogrupowanych danych
Jak obliczyć ranking percentylowy dla pogrupowanych danych