Jak używać metody łokcia w pythonie do znajdowania optymalnych klastrów

Jednym z najpopularniejszych algorytmów grupowania w uczeniu maszynowym jest grupowanie k-średnich .

Grupowanie K-średnich to technika, w której każdą obserwację ze zbioru danych umieszczamy w jednym z K klastrów.

Ostatecznym celem jest utworzenie K klastrów, w których obserwacje w każdym klastrze są do siebie dość podobne, podczas gdy obserwacje w różnych klastrach znacznie się od siebie różnią.

Wykonując grupowanie k-średnich, pierwszym krokiem jest wybranie wartości K – liczby skupień, w których chcemy umieścić obserwacje.

Jednym z najczęstszych sposobów wyboru wartości K jest metoda łokcia , która polega na utworzeniu wykresu zawierającego liczbę skupień na osi x i sumę kwadratów na osi y, a następnie zidentyfikowanie gdzie na działce pojawia się „kolano” lub zakręt.

Punkt na osi x, w którym występuje „kolano”, mówi nam o optymalnej liczbie skupień do wykorzystania w algorytmie grupowania k-średnich.

Poniższy przykład pokazuje, jak używać metody łokcia w Pythonie.

Krok 1: Zaimportuj niezbędne moduły

Najpierw zaimportujemy wszystkie moduły potrzebne do wykonania grupowania k-średnich:

 import pandas as pd
import numpy as np
import matplotlib. pyplot as plt
from sklearn. cluster import KMeans
from sklearn. preprocessing import StandardScaler

Krok 2: Utwórz ramkę danych

Następnie utworzymy ramkę danych zawierającą trzy zmienne dla 20 różnych koszykarzy:

 #createDataFrame
df = pd. DataFrame ({' points ': [18, np.nan, 19, 14, 14, 11, 20, 28, 30, 31,
                              35, 33, 29, 25, 25, 27, 29, 30, 19, 23],
                   ' assists ': [3, 3, 4, 5, 4, 7, 8, 7, 6, 9, 12, 14,
                               np.nan, 9, 4, 3, 4, 12, 15, 11],
                   ' rebounds ': [15, 14, 14, 10, 8, 14, 13, 9, 5, 4,
                                11, 6, 5, 5, 3, 8, 12, 7, 6, 5]})

#drop rows with NA values in any columns
df = df. dropna ()

#create scaled DataFrame where each variable has mean of 0 and standard dev of 1
scaled_df = StandardScaler(). fit_transform (df)

Krok 3: Użyj metody łokcia, aby znaleźć optymalną liczbę skupień

Załóżmy, że chcemy użyć grupowania k-średnich do grupowania podobnych aktorów na podstawie tych trzech wskaźników.

Aby wykonać grupowanie k-średnich w Pythonie, możemy użyć funkcji KMeans z modułu sklearn .

Najważniejszym argumentem tej funkcji jest n_clusters , który określa, w ilu klastrach umieścić obserwacje.

Aby określić optymalną liczbę skupień, utworzymy wykres przedstawiający liczbę skupień oraz SSE (suma kwadratów błędów) modelu.

Następnie będziemy szukać „kolana”, w którym suma kwadratów zaczyna się „wyginać” lub stabilizować. Punkt ten reprezentuje optymalną liczbę klastrów.

Poniższy kod pokazuje, jak utworzyć tego typu wykres, który wyświetla liczbę skupień na osi x i SSE na osi y:

 #initialize kmeans parameters
kmeans_kwargs = {
" init ": " random ",
" n_init ": 10,
" random_state ": 1,
}

#create list to hold SSE values for each k
sse = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, ** kmeans_kwargs)
    kmeans. fit (scaled_df)
    sse. append (kmeans.inertia_)

#visualize results
plt. plot (range(1, 11), sse)
plt. xticks (range(1, 11))
plt. xlabel (" Number of Clusters ")
plt. ylabel (“ SSE ”)
plt. show () 

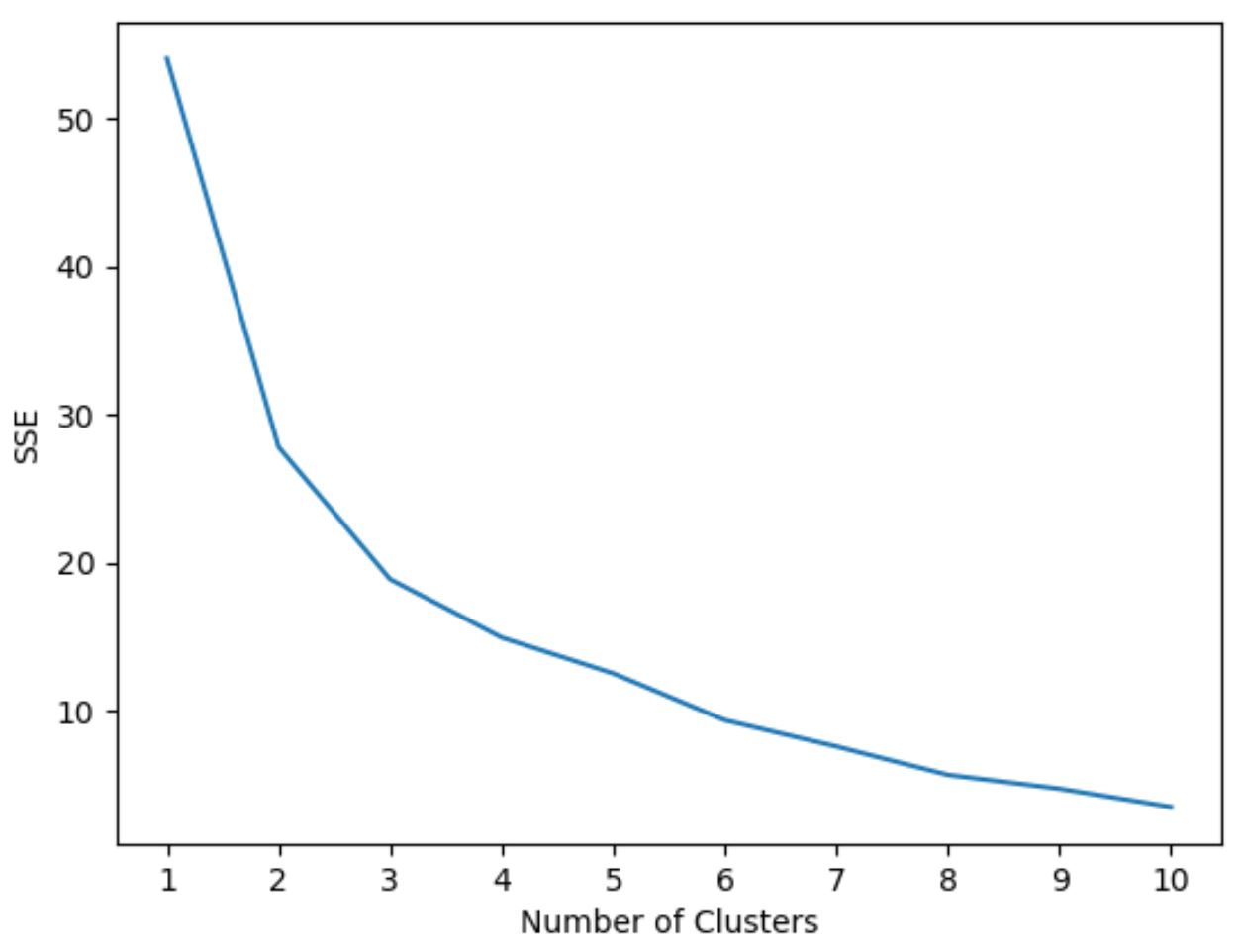
Na tym wykresie wydaje się, że w k = 3 skupiskach występuje załamanie lub „kolano”.

Zatem w następnym kroku podczas dopasowywania naszego modelu grupowania k-średnich użyjemy 3 klastrów.

Krok 4: Wykonaj grupowanie K-średnich z optymalnym K

Poniższy kod pokazuje, jak wykonać grupowanie k-średnich na zbiorze danych przy użyciu optymalnej wartości k z 3:

 #instantiate the k-means class, using optimal number of clusters
kmeans = KMeans(init=" random ", n_clusters= 3 , n_init= 10 , random_state= 1 )

#fit k-means algorithm to data
kmeans. fit (scaled_df)

#view cluster assignments for each observation
kmeans. labels_

array([1, 1, 1, 1, 1, 1, 2, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0]) 

Wynikowa tabela przedstawia przypisania klastrów dla każdej obserwacji w ramce DataFrame.

Aby ułatwić interpretację tych wyników, możemy dodać kolumnę do DataFrame, która pokazuje przypisanie każdego gracza do klastra:

 #append cluster assingments to original DataFrame
df[' cluster '] = kmeans. labels_

#view updated DataFrame
print (df)

points assists rebounds cluster
0 18.0 3.0 15 1
2 19.0 4.0 14 1
3 14.0 5.0 10 1
4 14.0 4.0 8 1
5 11.0 7.0 14 1
6 20.0 8.0 13 1
7 28.0 7.0 9 2
8 30.0 6.0 5 2
9 31.0 9.0 4 0
10 35.0 12.0 11 0
11 33.0 14.0 6 0
13 25.0 9.0 5 0
14 25.0 4.0 3 2
15 27.0 3.0 8 2
16 29.0 4.0 12 2
17 30.0 12.0 7 0
18 19.0 15.0 6 0
19 23.0 11.0 5 0

Kolumna klastra zawiera numer klastra (0, 1 lub 2), do którego przypisano każdego gracza.

Zawodnicy należący do tego samego skupienia mają w przybliżeniu podobne wartości kolumn punktów , asyst i zbiórek .

Uwaga : Pełną dokumentację funkcji KMeans sklearna znajdziesz tutaj .

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w Pythonie:

Jak wykonać regresję liniową w Pythonie
Jak przeprowadzić regresję logistyczną w Pythonie
Jak przeprowadzić weryfikację krzyżową K-Fold w Pythonie