Jak używać metody najmniejszych kwadratów w r

Metoda najmniejszych kwadratów to metoda, za pomocą której możemy znaleźć linię regresji, która najlepiej pasuje do danego zestawu danych.

Aby zastosować metodę najmniejszych kwadratów do dopasowania linii regresji w R, możemy użyć funkcji lm() .

Ta funkcja wykorzystuje następującą podstawową składnię:

 model <- lm(response ~ predictor, data=df)

Poniższy przykład pokazuje, jak używać tej funkcji w języku R.

Przykład: metoda najmniejszych kwadratów w R

Załóżmy, że mamy następującą ramkę danych w języku R, która pokazuje liczbę przepracowanych godzin i odpowiadający im wynik egzaminu dla 15 uczniów w klasie:

 #create data frame
df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of data frame
head(df)

  hours score
1 1 64
2 2 66
3 4 76
4 5 73
5 5 74
6 6 81

Możemy użyć funkcji lm() , aby zastosować metodę najmniejszych kwadratów w celu dopasowania linii regresji do tych danych:

 #use method of least squares to fit regression line
model <- lm(score ~ hours, data=df)

#view regression model summary
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min 1Q Median 3Q Max 
-5,140 -3,219 -1,193 2,816 5,772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 65,334 2,106 31,023 1.41e-13 ***
hours 1.982 0.248 7.995 2.25e-06 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared: 0.831, Adjusted R-squared: 0.818 
F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06

Z wartości w kolumnie Wynik szacunkowy możemy napisać następującą dopasowaną linię regresji:

Wynik egzaminu = 65,334 + 1,982 (godziny)

Oto jak interpretować każdy współczynnik w modelu:

• Intercept : Dla studenta studiującego 0 godzin oczekiwany wynik egzaminu to 65,334 .
• godziny : za każdą dodatkową godzinę nauki oczekiwany wynik egzaminu wzrasta o 1982 .

Możemy użyć tego równania, aby oszacować ocenę z egzaminu, jaką otrzyma uczeń na podstawie przepracowanych godzin.

Na przykład, jeśli student uczy się przez 5 godzin, szacujemy, że jego wynik egzaminu wyniesie 75,244:

Wynik egzaminu = 65,334 + 1,982(5) = 75,244

Na koniec możemy utworzyć wykres rozrzutu oryginalnych danych z dopasowaną linią regresji nałożoną na wykres:

 #create scatter plot of data
plot(df$hours, df$score, pch=16, col=' steelblue ')

#add fitted regression line to scatter plot
abline(model)

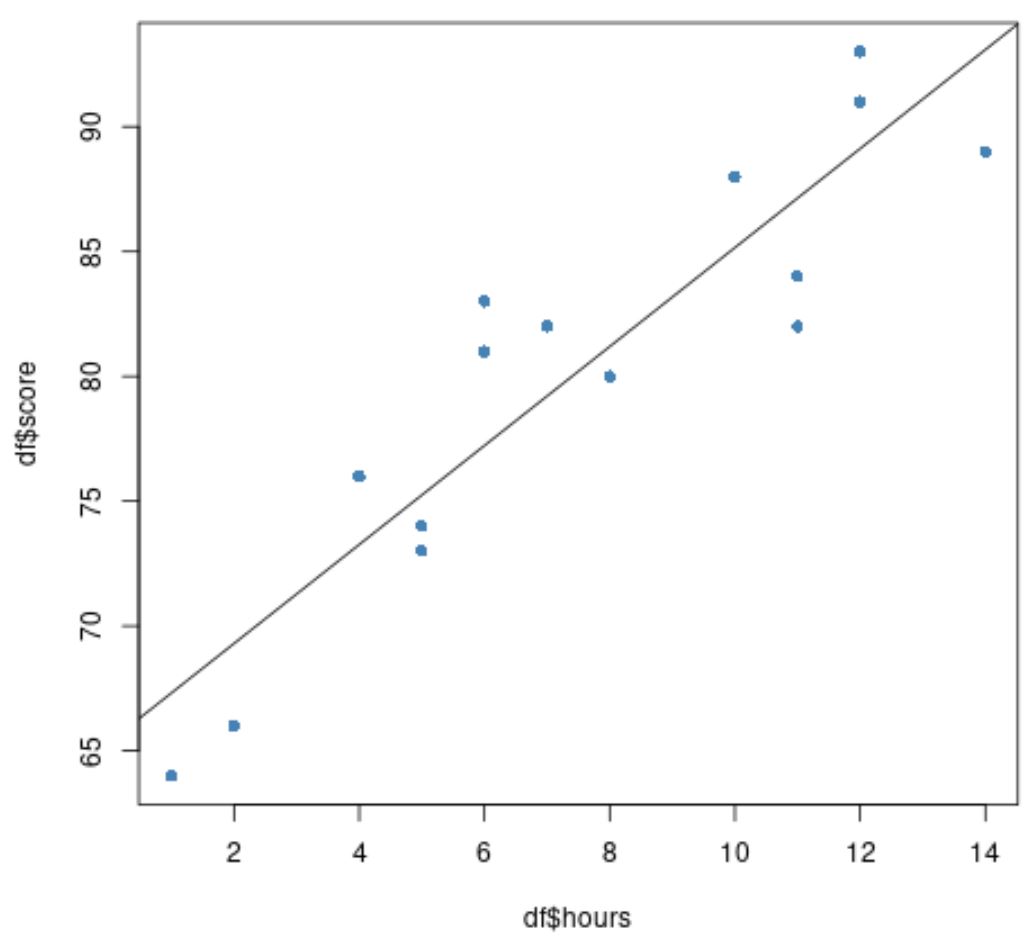
Niebieskie kółka przedstawiają dane, a czarna linia przedstawia dopasowaną linię regresji.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w języku R:

Jak utworzyć wykres rezydualny w R
Jak sprawdzić współliniowość w R
Jak wykonać dopasowanie krzywej w R