Miary tendencji centralnej: definicja i przykłady
Miarą tendencji centralnej jest pojedyncza wartość reprezentująca centralny punkt zbioru danych. Wartość tę można również nazwać „centralną lokalizacją” zbioru danych.
W statystyce istnieją trzy typowe miary tendencji centralnej:
- Średnia
- Mediana
- Moda
Każda z tych miar znajduje centralną lokalizację zbioru danych przy użyciu różnych metod. W zależności od rodzaju analizowanych danych lepszym rozwiązaniem może być użycie jednego z tych trzech wskaźników niż dwóch pozostałych.
W tym artykule przyjrzymy się, jak obliczyć każdą z trzech miar tendencji centralnej, a także jak określić, której miary najlepiej użyć na podstawie posiadanych danych.
Dlaczego miary tendencji centralnej są przydatne?
Zanim przyjrzymy się, jak obliczyć średnią, medianę i modę, warto przede wszystkim zrozumieć , dlaczego te pomiary są w ogóle przydatne.
Rozważ następujący scenariusz:
Młode małżeństwo zastanawia się, gdzie kupić swój pierwszy dom w nowym mieście, a maksymalna kwota, jaką może wydać, to 150 000 dolarów. W niektórych obszarach miasta znajdują się drogie domy, w innych tanie domy, a w jeszcze innych domy ze średniej półki cenowej. Chcą łatwo zawęzić wyszukiwanie do konkretnych dzielnic, które mieszczą się w ich budżecie.
Gdyby para spojrzała tylko na ceny domów jednorodzinnych w poszczególnych dzielnicach, mogłaby mieć trudności z określeniem, które dzielnice najlepiej odpowiadają ich budżetowi, ponieważ mogliby zobaczyć coś takiego:
Ceny domów w okolicy A : 140 000 USD, 190 000 USD, 265 000 USD, 115 000 USD, 270 000 USD, 240 000 USD, 250 000 USD, 180 000 USD, 160 000 USD, 200 000 USD, 240 000 USD, 280 000 USD…
Ceny domów w dzielnicy B : 140 000 USD, 290 000 USD, 155 000 USD, 165 000 USD, 280 000 USD, 220 000 USD, 155 000 USD, 185 000 USD, 160 000 USD, 200 000 USD, 190 000 USD, 140 000 USD, 145,0 USD 0 0,…
Ceny domów w dzielnicy C : 140 000 USD, 130 000 USD, 165 000 USD, 115 000 USD, 170 000 USD, 100 000 USD, 150 000 USD, 180 000 USD, 190 000 USD, 120 000 USD, 110 000 USD, 130 000 USD, 120,0 USD 0 0,…
Gdyby jednak znali średnią cenę (np. miarę tendencji centralnej) domów w każdej okolicy, mogliby znacznie szybciej zawęzić wyszukiwanie, ponieważ łatwiej byłoby im określić, w której dzielnicy ceny domów odpowiadają ich budżetowi:
Średnia cena domu w dzielnicy A: 220 000 dolarów
Średnia cena domu w dzielnicy B : 190 000 dolarów
Średnia cena domu w dzielnicy C : 140 000 dolarów
Znając średnią cenę domu w każdej okolicy, mogą szybko stwierdzić, że w dzielnicy C prawdopodobnie będzie dostępnych najwięcej domów w ramach ich budżetu.
Oto zaleta stosowania miary tendencji centralnej: pomaga zrozumieć centralną wartość zbioru danych, która zazwyczaj opisuje, gdzie zazwyczaj znajdują się wartości danych. W tym konkretnym przykładzie pomaga młodej parze zrozumieć typową cenę domu w każdej okolicy.
Na wynos: miara tendencji centralnej jest przydatna, ponieważ dostarcza nam jednej wartości opisującej „środek” zbioru danych. Pomaga nam to zrozumieć zbiór danych znacznie szybciej niż tylko przeglądanie wszystkich poszczególnych wartości w zbiorze danych.
Mieć na myśli
Najczęściej stosowaną miarą tendencji centralnej jest średnia . Aby obliczyć średnią zbioru danych, wystarczy dodać wszystkie poszczególne wartości i podzielić przez całkowitą liczbę wartości.
Średnia = (suma wszystkich wartości) / (całkowita liczba wartości)
Załóżmy na przykład, że mamy następujący zbiór danych pokazujący liczbę home runów zdobytych przez 10 graczy baseballowych tej samej drużyny w sezonie:
| Gracz | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dziesięć |
|---|---|---|---|---|---|---|---|---|---|---|
| Biegi do domu | 8 | 15 | 22 | 21 | 12 | 9 | 11 | 27 | 14 | 13 |
Średnią liczbę home runów trafionych na zawodnika można obliczyć w następujący sposób:
Średnia = (8+15+22+21+12+9+11+27+14+13) / 10 = 15,2 obwodów .
Mediana
Mediana to środkowa wartość zbioru danych. Medianę można znaleźć, uporządkując wszystkie poszczególne wartości w zbiorze danych od najmniejszej do największej i znajdując wartość mediany. Jeśli liczba wartości jest nieparzysta, medianą jest wartość środkowa. Jeśli liczba wartości jest parzysta, medianą jest średnia z dwóch wartości środkowych.
Na przykład, aby znaleźć średnią liczbę home runów zdobytych przez 10 graczy w baseball z poprzedniego przykładu, możemy uszeregować graczy w kolejności malejącej liczby home runów:
| Gracz | #1 | #6 | #7 | #5 | #dziesięć | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|---|
| Biegi do domu | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
Ponieważ mamy parzystą liczbę wartości, mediana jest po prostu średnią dwóch środkowych wartości: 13,5 .
Zamiast tego zastanówmy się, gdybyśmy mieli dziewięciu graczy:
| Gracz | #1 | #6 | #7 | #5 | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|
| Biegi do domu | 8 | 9 | 11 | 12 | 14 | 15 | 21 | 22 | 27 |
W tym przypadku, ponieważ mamy nieparzystą liczbę wartości, medianą jest po prostu wartość środkowa: 14 .
Moda
Tryb to wartość, która pojawia się najczęściej w zbiorze danych. Zbiór danych nie może mieć żadnych trybów (jeśli żadne wartości się nie powtarzają), jednego trybu lub wielu trybów.
Na przykład następujący zbiór danych nie ma trybu:
| Gracz | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dziesięć |
|---|---|---|---|---|---|---|---|---|---|---|
| Biegi do domu | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
Następujący zbiór danych ma tryb: 15 . Jest to wartość, która pojawia się najczęściej.
| Gracz | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dziesięć |
|---|---|---|---|---|---|---|---|---|---|---|
| Biegi do domu | 8 | 9 | 11 | 12 | 13 | 15 | 15 | 21 | 22 | 27 |
Poniższy zbiór danych ma trzy tryby: 8, 15, 19 . To właśnie te wartości pojawiają się najczęściej.
| Gracz | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dziesięć |
|---|---|---|---|---|---|---|---|---|---|---|
| Biegi do domu | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
Tryb może być szczególnie przydatną miarą tendencji centralnej podczas pracy z danymi kategorycznymi, ponieważ mówi nam, która kategoria pojawia się najczęściej. Rozważmy na przykład następujący wykres słupkowy przedstawiający wyniki ankiety dotyczącej ulubionego koloru ludzi:
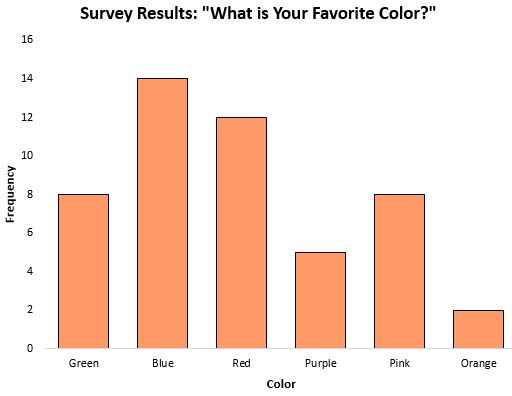
Tryb lub reakcja, która pojawiała się najczęściej, była niebieska.
W scenariuszach, w których dane są kategoryczne (jak ten powyżej), nie jest nawet możliwe obliczenie mediany ani średniej, więc moda jest jedyną miarą tendencji centralnej, której możemy użyć.
Tryb ten może być również używany do danych liczbowych, jak widzieliśmy w powyższym przykładzie z graczami w baseball. Jednakże tryb wydaje się być mniej przydatny przy udzielaniu odpowiedzi na pytanie „Jaka jest typowa wartość dla tego zbioru danych?” »
Załóżmy na przykład, że chcemy poznać typową liczbę home runów trafionych przez gracza baseballowego w tej drużynie:
| Gracz | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dziesięć |
|---|---|---|---|---|---|---|---|---|---|---|
| Biegi do domu | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
Tryb dla tego zbioru danych to 8, 15 i 19, ponieważ są to najczęstsze wartości. Jednak nie są one zbyt pomocne w zrozumieniu typowej liczby home runów trafianych przez gracza w drużynie. Lepszą miarą tendencji centralnej byłaby w tym przypadku mediana (15) lub średnia (również 15).
Tryb jest również słabą miarą tendencji centralnej, gdy jest liczbą odległą od pozostałych wartości. Na przykład następujący tryb zbioru danych to 30, ale w rzeczywistości nie reprezentuje to „typowej” liczby home runów na zawodnika w drużynie:
| Gracz | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dziesięć |
|---|---|---|---|---|---|---|---|---|---|---|
| Biegi do domu | 5 | 6 | 7 | dziesięć | 11 | 12 | 13 | 15 | 30 | 30 |
Ponownie, średnia lub mediana lepiej opisałaby centralną lokalizację tego zbioru danych.
Kiedy stosować średnią, medianę i tryb
Widzieliśmy, że średnia, mediana i mod mierzą centralną lokalizację, czyli „typową wartość” zbioru danych na bardzo różne sposoby:
Średnia: znajduje średnią wartość w zestawie danych.
Mediana: znajduje wartość mediany w zestawie danych.
Tryb: znajduje najczęstszą wartość w zestawie danych.
Oto scenariusze, w których lepiej zastosować pewne miary tendencji centralnej niż inne:
Kiedy stosować średnią
Najlepiej jest używać średniej, gdy rozkład danych jest dość symetryczny i nie ma wartości odstających.
Załóżmy na przykład, że mamy następujący rozkład pokazujący wynagrodzenia osób w określonym mieście:
Ponieważ rozkład ten jest dość symetryczny (tzn. jeśli podzieli się go na pół, każda połowa będzie wyglądać mniej więcej tak samo) i nie ma żadnych wartości odstających (tj. (powiedzmy, że nie ma wyjątkowo wysokich wynagrodzeń), średnia dobrze opisze ten zbiór danych.
Średnia wynosi 63 000 dolarów, co stanowi mniej więcej środek rozkładu:
Kiedy stosować medianę
Najlepiej jest używać mediany, gdy rozkład danych jest skośny lub gdy występują wartości odstające.
stronnicze dane:
Kiedy rozkład jest przekrzywiony, medianie nadal udaje się uchwycić położenie centralne. Rozważmy na przykład następujący rozkład wynagrodzeń osób w określonym mieście:
Mediana lepiej odzwierciedla „typową” pensję danej osoby niż średnia. Dzieje się tak, ponieważ duże wartości na końcu rozkładu mają tendencję do przesuwania średniej od środka w kierunku długiego ogona.
W tym konkretnym przykładzie średnia mówi nam, że typowa osoba zarabia w tym mieście około 47 000 dolarów rocznie, podczas gdy mediana mówi nam, że typowa osoba zarabia tylko około 32 000 dolarów rocznie, co jest znacznie bardziej reprezentatywne dla typowej osoby.
Wartości odstające:
Mediana pomaga również lepiej uchwycić centralną lokalizację rozkładu, gdy w danych występują wartości odstające. Rozważmy na przykład poniższy wykres przedstawiający powierzchnię domów przy określonej ulicy:
Na średnią duży wpływ ma kilka niezwykle dużych domów, podczas gdy na medianę nie. Zatem mediana lepiej oddaje „typową” powierzchnię domu przy tej ulicy niż średnia.
Kiedy używać trybu
Tego trybu najlepiej używać, gdy pracujesz z danymi kategorycznymi i chcesz wiedzieć, która kategoria pojawia się najczęściej. Oto kilka przykładów:
- Przeprowadzasz ankietę na temat ulubionych kolorów ludzi i chcesz wiedzieć, który kolor pojawia się najczęściej w odpowiedziach.
- Przeprowadzasz badanie preferencji ludzi wśród trzech opcji projektowania stron internetowych i chcesz wiedzieć, który projektanci preferują najbardziej.
Jak wspomniano wcześniej, jeśli pracujesz z danymi kategorycznymi, nie jest nawet możliwe obliczenie mediany lub średniej, co pozostawia modę jako jedyną miarę tendencji centralnej.
Ogólnie rzecz biorąc, jeśli pracujesz z danymi liczbowymi, takimi jak powierzchnia domów, liczba home runów zdobytych na zawodnika, wynagrodzenie na osobę itp., zazwyczaj najlepiej jest użyć mediany lub średniej, aby opisać wartość „typową” w zbiór danych.
Uwaga: Należy zauważyć, że jeśli zbiór danych ma rozkład całkowicie normalny, wówczas średnia, mediana i moda mają tę samą wartość.
o autorze
Dr Benjamin Anderson
Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej