Częściowe najmniejsze kwadraty w pythonie (krok po kroku)

Jednym z najczęstszych problemów, jakie można napotkać w uczeniu maszynowym, jest wieloliniowość . Dzieje się tak, gdy dwie lub więcej zmiennych predykcyjnych w zbiorze danych jest silnie skorelowanych.

Kiedy tak się stanie, model może być w stanie dobrze dopasować zbiór danych uczących, ale może działać słabo na nowym zbiorze danych, którego nigdy nie widział, ponieważ nadmiernie pasuje do zbioru danych uczących. zestaw treningowy.

Jednym ze sposobów obejścia tego problemu jest zastosowanie metody zwanej cząstkowymi najmniejszymi kwadratami , która działa w następujący sposób:

• Standaryzacja zmiennych predykcyjnych i odpowiedzi.
• Oblicz M kombinacji liniowych (zwanych „składnikami PLS”) p oryginalnych zmiennych predykcyjnych, które wyjaśniają znaczną ilość zmian zarówno w zmiennej odpowiedzi, jak i zmiennych predykcyjnych.
• Użyj metody najmniejszych kwadratów, aby dopasować model regresji liniowej, używając komponentów PLS jako predyktorów.
• Użyj k-krotnej walidacji krzyżowej , aby znaleźć optymalną liczbę komponentów PLS do utrzymania w modelu.

Ten samouczek zawiera przykład krok po kroku wykonywania częściowych najmniejszych kwadratów w Pythonie.

Krok 1: Zaimportuj niezbędne pakiety

Najpierw zaimportujemy pakiety potrzebne do wykonania częściowej metody najmniejszych kwadratów w Pythonie:

 import numpy as np
import pandas as pd
import matplotlib. pyplot as plt
from sklearn. preprocessing import scale 
from sklearn import model_selection
from sklearn. model_selection import RepeatedKFold
from sklearn. model_selection import train_test_split
from sklearn. cross_decomposition import PLSRegression
from sklearn . metrics import mean_squared_error

Krok 2: Załaduj dane

W tym przykładzie użyjemy zbioru danych o nazwie mtcars , który zawiera informacje o 33 różnych samochodach. Użyjemy hp jako zmiennej odpowiedzi i następujących zmiennych jako predyktorów:

• mpg
• wyświetlacz
• gówno
• waga
• sek

Poniższy kod pokazuje, jak załadować i wyświetlić ten zestaw danych:

 #define URL where data is located
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/mtcars.csv"

#read in data
data_full = pd. read_csv (url)

#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]

#view first six rows of data
data[0:6]


        mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105

Krok 3: Dopasuj model częściowych najmniejszych kwadratów

Poniższy kod pokazuje, jak dopasować model PLS do tych danych.

Zauważ, że cv = RepeatedKFold() mówi Pythonowi, aby użył k-krotnej walidacji krzyżowej do oceny wydajności modelu. W tym przykładzie wybieramy k = 10 fałd, powtórzonych 3 razy.

 #define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]

#define cross-validation method
cv = RepeatedKFold(n_splits= 10 , n_repeats= 3 , random_state= 1 )

mse = []
n = len (X)

# Calculate MSE with only the intercept
score = -1*model_selection. cross_val_score (PLSRegression(n_components=1),
n.p. ones ((n,1)), y, cv=cv, scoring=' neg_mean_squared_error '). mean ()    
mse. append (score)

# Calculate MSE using cross-validation, adding one component at a time
for i in np. arange (1, 6):
    pls = PLSRegression(n_components=i)
    score = -1*model_selection. cross_val_score (pls, scale(X), y, cv=cv,
               scoring=' neg_mean_squared_error '). mean ()
    mse. append (score)

#plot test MSE vs. number of components
plt. plot (mse)
plt. xlabel (' Number of PLS Components ')
plt. ylabel (' MSE ')
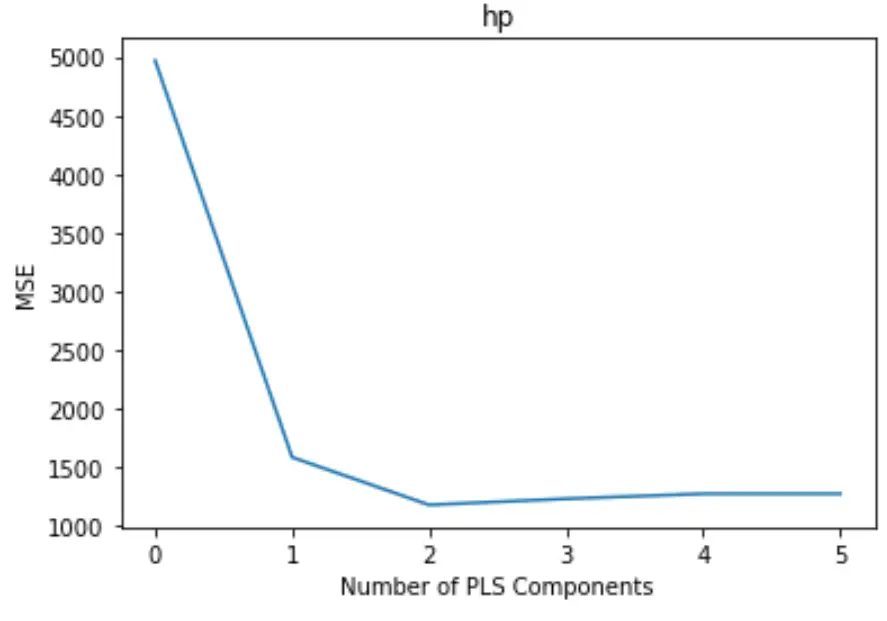
plt. title (' hp ')

Wykres przedstawia liczbę komponentów PLS wzdłuż osi x oraz test MSE (średni błąd kwadratowy) wzdłuż osi y.

Z wykresu widzimy, że MSE testu zmniejsza się po dodaniu dwóch składników PLS, ale zaczyna rosnąć po dodaniu więcej niż dwóch składników PLS.

Zatem optymalny model obejmuje tylko dwa pierwsze elementy PLS.

Krok 4: Użyj ostatecznego modelu do przewidywania

Możemy wykorzystać ostateczny model PLS z dwoma komponentami PLS do przewidywania nowych obserwacji.

Poniższy kod pokazuje, jak podzielić oryginalny zbiór danych na zbiór uczący i testowy oraz użyć modelu PLS z dwoma komponentami PLS do przewidywania zbioru testowego.

 #split the dataset into training (70%) and testing (30%) sets
X_train , _

#calculate RMSE
pls = PLSRegression(n_components=2)
pls. fit (scale(X_train), y_train)

n.p. sqrt (mean_squared_error(y_test, pls. predict (scale(X_test))))

29.9094

Widzimy, że RMSE testu wynosi 29,9094 . Jest to średnie odchylenie pomiędzy przewidywaną wartością KM a obserwowaną wartością KM dla obserwacji zestawu testowego.

Pełny kod Pythona użyty w tym przykładzie można znaleźć tutaj .