Najmniej znacząca różnica fishera: definicja + przykład

Jednoczynnikową ANOVA stosuje się do określenia, czy istnieje statystycznie istotna różnica pomiędzy średnimi z trzech lub więcej niezależnych grup.

Założenia stosowane w ANOVA są następujące:

H ₀ : Średnie są równe dla każdej grupy.

H _A : Przynajmniej jeden ze sposobów różni się od pozostałych.

Jeśli wartość p analizy ANOVA jest poniżej pewnego poziomu istotności (takiego jak α = 0,05), możemy odrzucić hipotezę zerową i stwierdzić, że przynajmniej jedna ze średnich grupowych różni się od pozostałych.

Aby jednak dokładnie wiedzieć, które grupy się od siebie różnią, musimy przeprowadzić test post hoc.

Powszechnie stosowanym testem post hoc jest test najmniejszej znaczącej różnicy Fishera .

Aby wykonać ten test, najpierw obliczamy następującą statystykę testową:

LSD = t _0,025 , _{DF w} * √ MS _W (1/n ₁ + 1/n ₁ )

Złoto:

• t _.025 , _DFw : Wartość krytyczna t tabeli rozkładu t przy α = .025 i DF _w odpowiada stopniom swobody w obrębie grup tabeli ANOVA.
• MS _W : Średnie kwadraty w grupach w tabeli ANOVA.
• n ₁ , n ₂ : Wielkość próby w każdej grupie

Następnie możemy porównać średnią różnicę między każdą grupą z tą statystyką testową. Jeżeli wartość bezwzględna średniej różnicy między dwiema grupami jest większa niż statystyka testowa, możemy stwierdzić, że istnieje statystycznie istotna różnica między średnimi grupowymi.

Poniższy przykład pokazuje, jak w praktyce przeprowadzić test najmniejszych znaczących różnic Fishera.

Przykład: Test różnicy najmniejszej istotności Fishera

Załóżmy, że profesor chce wiedzieć, czy trzy różne techniki uczenia się prowadzą do różnych wyników testów wśród studentów. Aby to sprawdzić, losowo przydziela 10 uczniów do stosowania każdej techniki uczenia się i rejestruje wyniki ich egzaminów.

Poniższa tabela przedstawia wyniki egzaminów każdego ucznia w oparciu o zastosowaną technikę nauki:

Profesor przeprowadza jednokierunkową ANOVA i otrzymuje następujące wyniki:

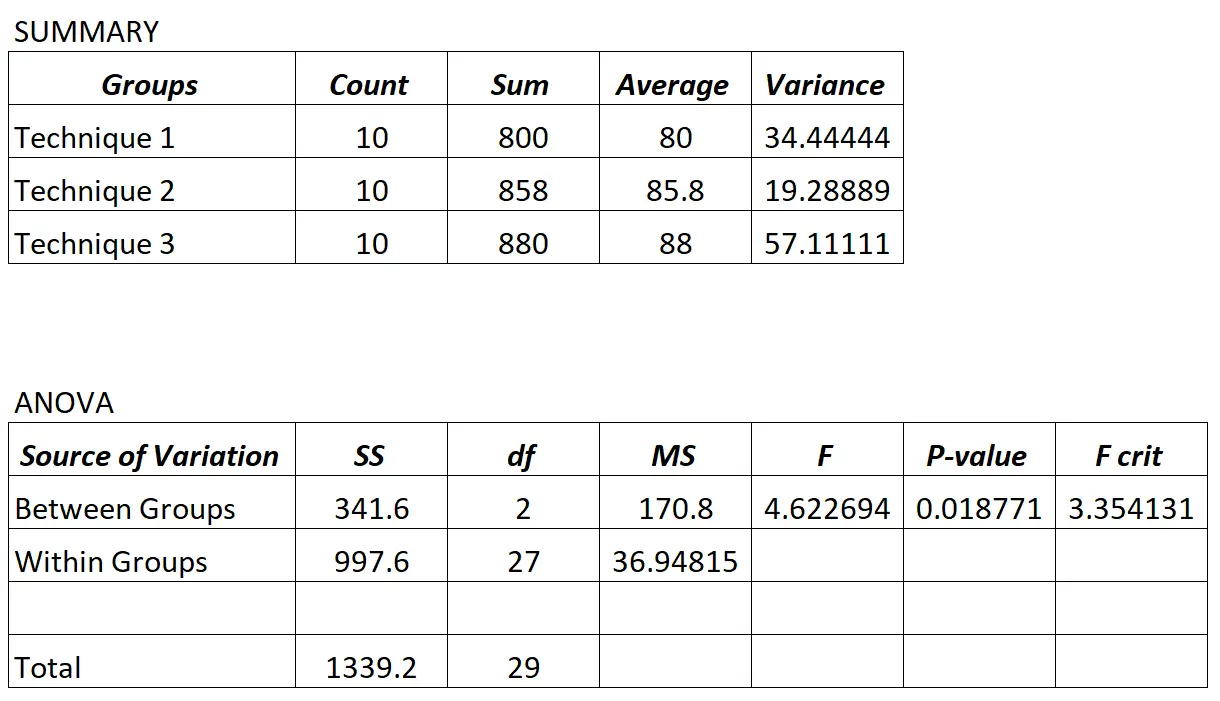
Ponieważ wartość p w tabeli ANOVA (0,018771) jest mniejsza niż 0,05, możemy stwierdzić, że wszystkie średnie wyniki egzaminów pomiędzy trzema grupami nie są równe.

Możemy zatem wykonać test najmniejszych znaczących różnic Fishera, aby określić, które średnie grupowe są różne.

Korzystając z wartości z wyniku ANOVA, możemy obliczyć statystykę testu Fishera w następujący sposób:

• LSD = t _0,025 , _DFw * √ MS _W (1/n ₁ + 1/n ₁ )
• LSD = t _0,025 , ₂₇ * √ 36,948*(1/10 + 1/10)
• LSD = 2,052 * √ 7,3896
• LSD = 5,578

Następnie możemy obliczyć średnią bezwzględną różnicę między każdą grupą:

• Technika 1 kontra Technika 2: |80 – 85,8| = 5,8
• Technika 1 kontra Technika 3: |80 – 88| = 8
• Technika 2 kontra Technika 3: |85,8 – 88| = 2,2

Średnie bezwzględne różnice między techniką 1 a techniką 2 oraz między techniką 1 a techniką 3 są większe niż statystyki testu Fishera. Można zatem stwierdzić, że techniki te prowadzą do statystycznie istotnie odmiennych średnich ocen z egzaminów.

Możemy również stwierdzić, że nie ma znaczącej różnicy w średnich wynikach egzaminu pomiędzy techniką 2 i techniką 3.