Dolne kwadraty

Przez Benjamin Anderson 2 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniono, czym jest metoda najmniejszych kwadratów w statystyce, na czym polega metoda najmniejszych kwadratów i w jaki sposób model regresji jest dopasowywany za pomocą kryterium najmniejszych kwadratów.

Na czym polega metoda najmniejszych kwadratów?

Metoda najmniejszych kwadratów to metoda statystyczna stosowana do wyznaczania równania regresji. Inaczej mówiąc, metoda najmniejszych kwadratów jest kryterium stosowanym w modelu regresji w celu minimalizacji błędu uzyskanego przy obliczaniu równania regresji.

Konkretnie metoda najmniejszych kwadratów polega na minimalizowaniu sumy kwadratów reszt, czyli innymi słowy polega na minimalizowaniu sumy kwadratów różnic pomiędzy wartościami przewidywanymi przez model regresji a wartościami obserwowanymi . . Poniżej zobaczymy szczegółowo, jak model regresji jest dopasowywany za pomocą kryterium najmniejszych kwadratów.

Główną cechą metody najmniejszych kwadratów jest to, że minimalizowane są najdłuższe odległości między obserwowanymi wartościami a funkcją regresji. W przeciwieństwie do innych kryteriów regresji, metoda najmniejszych kwadratów uważa, że ważniejsze jest minimalizowanie dużych reszt niż małych reszt, ponieważ kwadrat dużej liczby jest znacznie większy niż kwadrat małej. numer.

Błąd szacunkowy

Aby w pełni zrozumieć koncepcję najmniejszych kwadratów, musimy najpierw jasno określić, jakie reszty znajdują się w modelu regresji. Dlatego poniżej zobaczymy, czym jest błąd oszacowania i jak jest obliczany.

W statystyce błąd estymacji , zwany także rezydualnym , jest różnicą między wartością prawdziwą a wartością dopasowaną przez model regresji. Resztę statystyczną oblicza się zatem w następujący sposób:

$e_i=y_i-\widehat{y}_i$

Złoto:

$e_i$

jest resztą danych i.
$y_i$

to rzeczywista wartość danych, tj.
$\widehat{y}_i$

to wartość podana przez model regresji dla danych, tj.

Zatem im większa reszta fragmentu danych, tym słabiej model regresji jest dostosowany do tego fragmentu danych. Zatem im mniejsza reszta, tym mniejsza odległość między jej rzeczywistą wartością a wartością przewidywaną.

Podobnie, jeśli reszta fragmentu danych jest dodatnia, oznacza to, że model regresji przewiduje wartość niższą od wartości prawdziwej. natomiast jeśli reszta jest ujemna, oznacza to, że wartość przewidywana jest większa niż wartość rzeczywista.

Minimalizuj kwadraty błędów

Teraz, gdy wiemy, czym jest reszta w statystyce, łatwiej będzie zrozumieć, w jaki sposób minimalizowane są kwadraty błędów.

Kwadrat błędu jest kwadratem reszty, zatem kwadrat błędu jest równy różnicy między wartością prawdziwą a wartością dopasowaną przez model regresji podniesioną do potęgi dwójki.

$e_i^2=(y_i-\widehat{y}_i)^2$

Złoto:

$e_i^2$

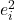
jest kwadratem reszty danych i.
$y_i$

to rzeczywista wartość danych, tj.
$\widehat{y}_i$

to wartość podana przez model regresji dla danych, tj.

Zatem metoda najmniejszych kwadratów polega na utworzeniu modelu regresji poprzez minimalizację sumy kwadratów błędów . Kryterium najmniejszych kwadratów opiera się zatem na minimalizacji wyrażenia:

$\begin{array}{l} [MIN] \ \displaystyle \sum_{i=1}^ne_i^2\\[4ex][MIN] \ \displaystyle \sum_{i=1}^n(y_i-\widehat{y}_i)^2\end{array}$

Dlatego też kryterium najmniejszych kwadratów nazywane jest także kryterium najmniejszych kwadratów.

Jak widać z poprzedniego wzoru, kryterium najmniejszych kwadratów przywiązuje większą wagę do minimalizacji dużych reszt niż małych reszt. Na przykład, jeśli jedna reszta wynosi 3, a druga reszta wynosi 5, ich kwadraty wynoszą odpowiednio 9 i 25, więc kryterium najmniejszych kwadratów będzie priorytetem minimalizacji drugiej reszty przed pierwszą resztą.

Regulacja metodą najmniejszych kwadratów

Dopasowanie modelu regresji przy użyciu kryterium najmniejszych kwadratów polega na znalezieniu modelu regresji, który minimalizuje kwadraty reszt. Zatem równaniem otrzymanym z modelu regresji będzie takie, którego kwadraty różnic pomiędzy wartościami obserwowanymi a wartościami dopasowanymi są minimalne.

W poniższym przykładzie należy zauważyć, że istnieje więcej kryteriów tworzenia modelu regresji i w zależności od wybranego kryterium równanie regresji jest inne.

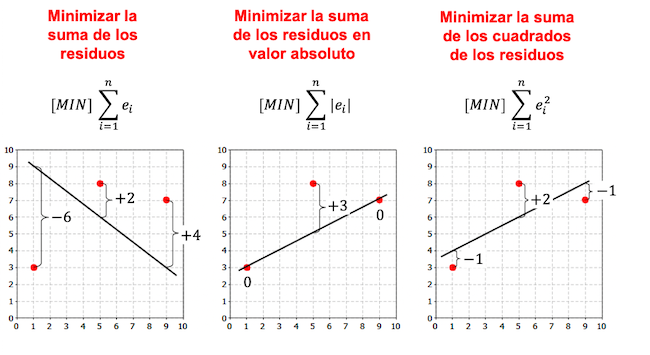
metoda najmniejszych kwadratów, dopasowanie metodą najmniejszych kwadratów

Jak widać na poprzednich przykładach, linia uzyskana z modelu regresji liniowej dla tego samego zbioru danych zależy od wybranego kryterium. Generalnie w modelach regresji stosuje się kryterium najmniejszych kwadratów.

W statystyce najczęściej stosowanym modelem regresji jest prosty model regresji liniowej, który polega na aproksymacji zależności pomiędzy zmienną niezależną X i zmienną zależną Y za pomocą linii prostej.

$y=b_0+b_1x$

Zatem wzory na dopasowanie zbioru danych do prostego modelu regresji liniowej są następujące:

$b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}$

$b_0=\overline{y}-b_1\overline{x}$

Przykład obliczenia prostego modelu regresji liniowej przy użyciu kryterium najmniejszych kwadratów można zobaczyć, klikając poniższy link:

➤ Zobacz: Przykład prostej regresji liniowej

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej