Jak tworzyć i interpretować wykresy qq w stata

Wykres QQ , skrót od „kwantyl-kwantyl”, jest często używany do oceny, czy reszty z analizy regresji mają rozkład normalny, czy nie.

W tym samouczku wyjaśniono, jak utworzyć i zinterpretować wykres QQ w Stata.

Przykład: wykres QQ w Stata

W tym przykładzie użyjemy automatycznego zbioru danych wbudowanego w Stata. Dopasujemy model regresji liniowej, wykorzystując mpg i przemieszczenie jako zmienne objaśniające oraz cenę jako zmienną odpowiedzi. Następnie uzyskamy reszty dla modelu i utworzymy wykres QQ, aby sprawdzić, czy reszty mają rozkład normalny.

Krok 1: Załaduj i wyświetl dane.

Najpierw załadujemy dane za pomocą następującego polecenia:

automatyczne korzystanie z systemu

Następnie uzyskamy szybkie podsumowanie danych za pomocą następującego polecenia:

podsumować

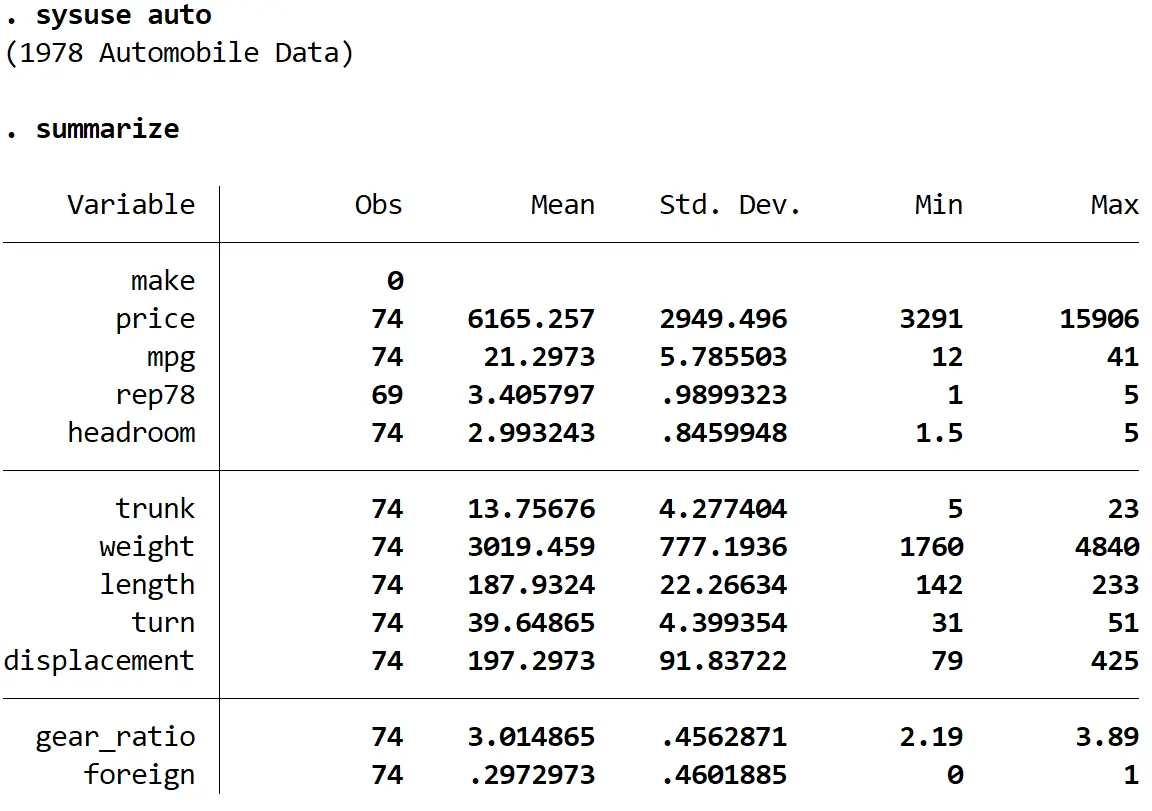
Krok 2: Dopasuj model regresji.

Następnie użyjemy następującego polecenia, aby dopasować model regresji:

regresja cena mpg przemieszczenie

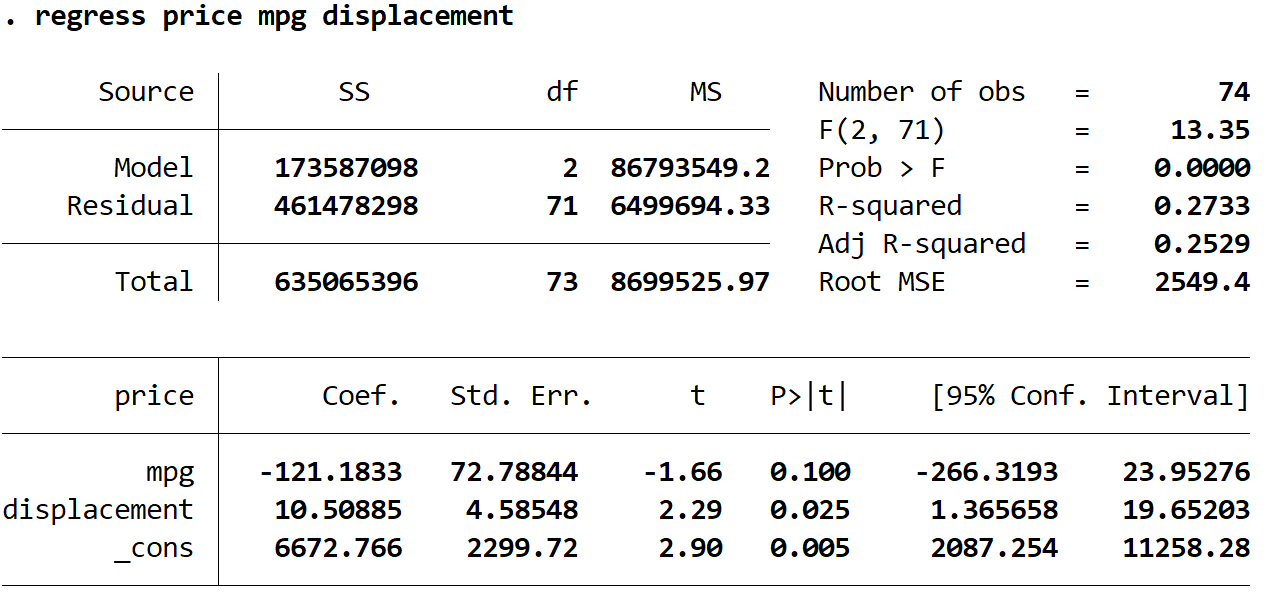
Krok 3: Oblicz reszty .

Przypomnijmy, że reszta to po prostu różnica między przewidywaną wartością odpowiedzi (obliczoną za pomocą oszacowanego równania regresji) a rzeczywistą wartością odpowiedzi.

Reszty każdej prognozy możemy uzyskać za pomocą polecenia reszt i przechowując te wartości w zmiennej o dowolnej nazwie. W tym przypadku użyjemy nazwy resid_price :

przewidzieć cenę_rezydencji, pozostałości

Krok 4: Utwórz wykres QQ.

Teraz, gdy mamy listę reszt, możemy utworzyć wykres QQ za pomocą polecenia qnorm :

qnorm cena_rezydencja

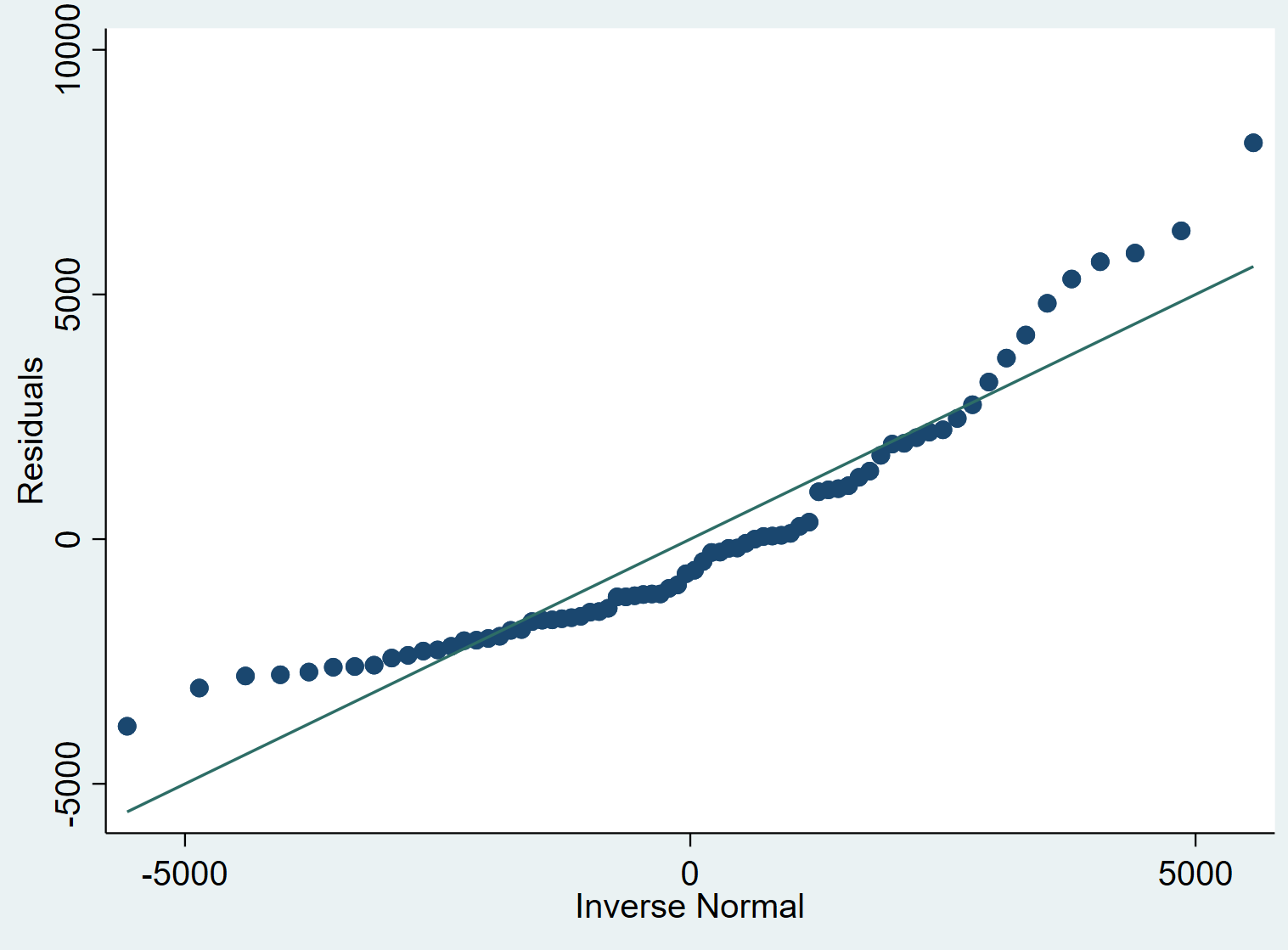
Krok 5: Zinterpretuj wykres QQ.

Idea wykresu QQ jest prosta: jeśli reszty układają się w przybliżeniu po linii prostej pod kątem 45 stopni, wówczas reszty mają w przybliżeniu rozkład normalny. Na powyższym wykresie QQ widzimy, że reszty mają tendencję do odbiegania nieco od linii 45 stopni, szczególnie na końcach, co może wskazywać, że nie mają one rozkładu normalnego.

Chociaż wykres QQ nie jest formalnym testem statystycznym, zapewnia prosty sposób wizualnego sprawdzenia, czy reszty mają rozkład normalny, czy nie.

Jeśli okaże się, że reszty znacznie odbiegają od linii 45 stopni na wykresie QQ, można rozważyć wykonanie transformacji zmiennej odpowiedzi w regresji, na przykład przy użyciu pierwiastka kwadratowego lub logu zmiennej odpowiedzi.

Jeśli reszty różnią się tylko nieznacznie, nie trzeba się martwić o transformację zmiennej odpowiedzi, ponieważ regresja jest dość odporna na odchylenia od normalności.