Normalna dystrybucja

Przez Benjamin Anderson 3 sierpnia, 2023 Prawdopodobieństwo 0 komentarzy

W tym artykule wyjaśniono, czym jest rozkład normalny w statystyce. Znajdziesz więc definicję rozkładu normalnego, przykłady rozkładów normalnych i jakie są właściwości rozkładu normalnego.

Jaki jest rozkład normalny?

Rozkład normalny to ciągły rozkład prawdopodobieństwa, którego wykres ma kształt dzwonu i jest symetryczny względem średniej. W statystyce rozkład normalny służy do modelowania zjawisk o bardzo różnych charakterystykach, dlatego ten rozkład jest tak ważny.

W rzeczywistości w statystyce rozkład normalny jest zdecydowanie najważniejszym rozkładem wszystkich rozkładów prawdopodobieństwa, ponieważ nie tylko może modelować dużą liczbę zjawisk w świecie rzeczywistym, ale rozkład normalny można również wykorzystać do aproksymacji innych typów rozkładów dystrybucje. pod pewnymi warunkami.

Symbolem rozkładu normalnego jest wielka litera N. Zatem, aby wskazać, że zmienna ma rozkład normalny, jest ona oznaczona literą N, a wartości jej średniej arytmetycznej i odchylenia standardowego są dodawane w nawiasach.

$X\sim N(\mu,\sigma)$

Rozkład normalny ma wiele różnych nazw, w tym rozkład Gaussa , rozkład Gaussa i rozkład Laplace’a-Gaussa .

Przykłady rozkładów normalnych

Zazwyczaj zbiory danych o rozkładzie normalnym zawierają dużą liczbę obserwacji i obejmują bardzo ogólne tematy. Poniżej znajduje się kilka przykładów próbek statystycznych, które ogólnie można modelować za pomocą rozkładu normalnego.

Przykłady rozkładu normalnego:

Liczba uczniów na kursie.
IQ pracowników firmy.
Liczba wadliwych części wyprodukowanych w fabryce w ciągu jednego dnia.
Oceny uzyskane na egzaminie przez studentów kursu.
Rentowność akcji spółek notowanych na giełdzie.

Wykres rozkładu normalnego

Kiedy już zobaczyliśmy, czym jest rozkład normalny i kilka przykładów tego typu rozkładu prawdopodobieństwa, zobaczmy, jak wygląda jego wykres, aby lepiej zrozumieć tę koncepcję.

Na poniższym wykresie można zobaczyć, jak zmienia się funkcja gęstości rozkładu normalnego w zależności od wartości jego średniej arytmetycznej i odchylenia standardowego.

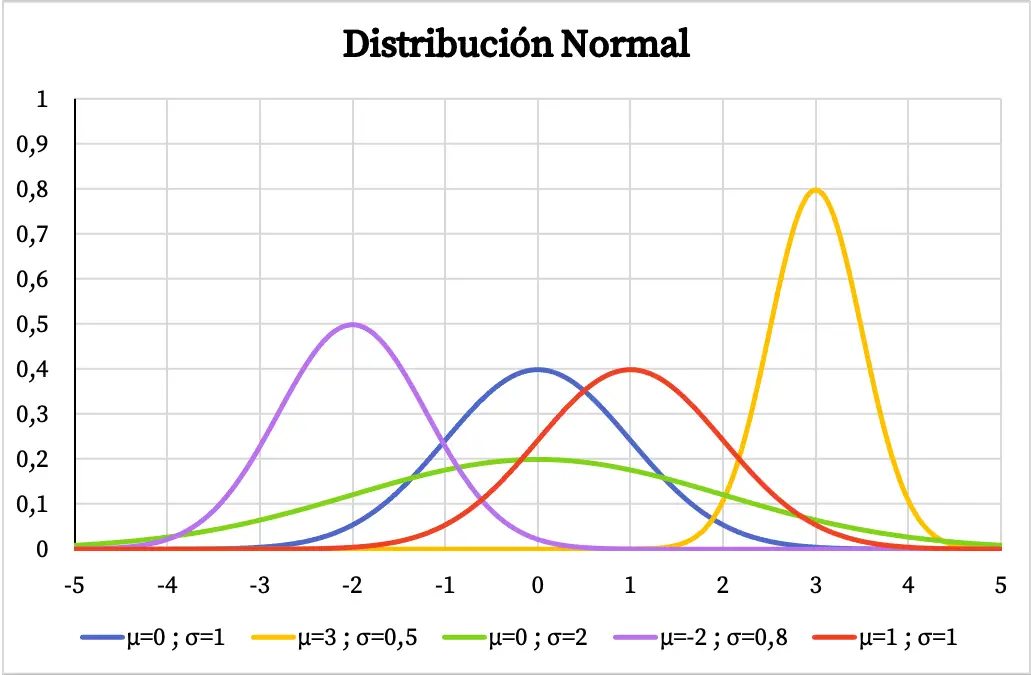
Mając kształt dzwonu wyśrodkowany na średniej arytmetycznej, jeśli zmienna ma rozkład normalny, oznacza to, że najczęściej powtarzającą się wartością jest średnia, a wartości wokół średniej powtarzają się częściej niż wartości ekstremalne. Podobnie, im większe odchylenie standardowe rozkładu normalnego, tym bardziej płaski jest kształt jego graficznej reprezentacji.

Z drugiej strony wykres skumulowanej funkcji prawdopodobieństwa rozkładu normalnego zależy również od wartości jego średniej arytmetycznej i odchylenia standardowego, jak widać na poniższym obrazku:

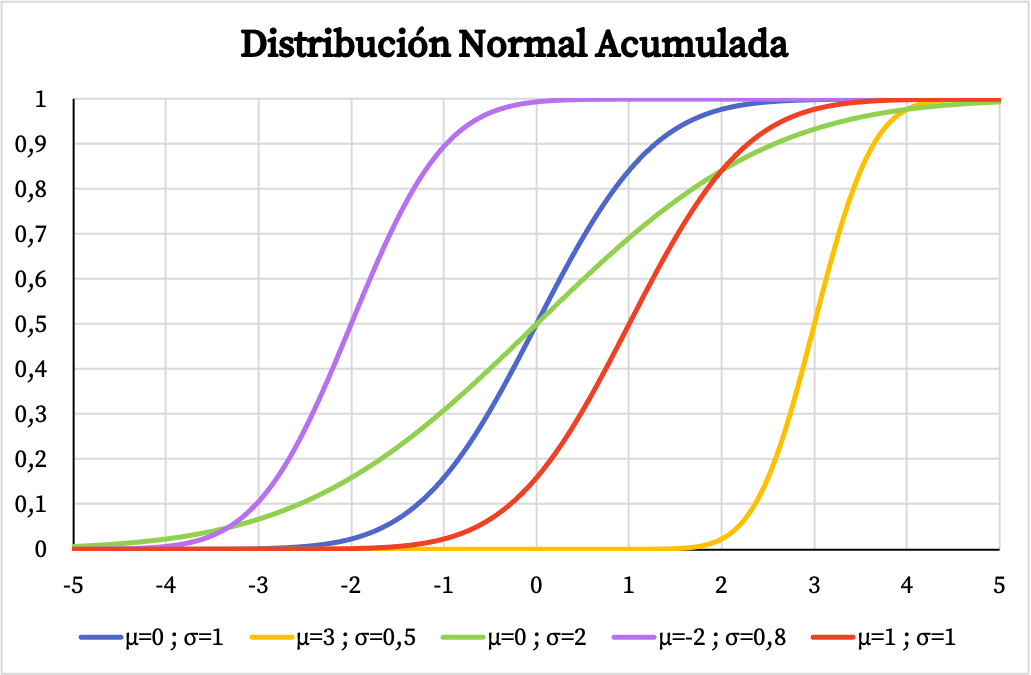
Funkcja gęstości i dystrybuanta rozkładu normalnego umożliwiają obliczenie prawdopodobieństw związanych z tym rozkładem. Zamiast jednak używać ich formuł, można bezpośrednio skorzystać z tabel rozkładu normalnego, ponieważ jest to szybsze. Z tabelami można zapoznać się pod następującym linkiem:

➤ Zobacz: Tabela rozkładu normalnego

Charakterystyka rozkładu normalnego

Rozkład normalny ma następujące cechy:

Rozkład normalny zależy od dwóch charakterystycznych parametrów, którymi są jego średnia arytmetyczna (μ) i odchylenie standardowe (σ).

$X\sim N(\mu,\sigma)$

Rozkład normalny może przyjmować wartości dodatnie i ujemne, zatem dziedziną rozkładu normalnego są liczby rzeczywiste.

$x\in \mathbb{R}$

Mediana i postać rozkładu normalnego są równe średniej arytmetycznej rozkładu.

$Me=Mo=\mu$

Współczynnik skośności i współczynnik kurtozy rozkładu normalnego wynoszą zero.

$\begin{array}{c}A=0\\[2ex]C=0\end{array}$

Wzór na funkcję gęstości rozkładu normalnego to:

$\displaystyle P[X=x]=\frac1{\sigma\sqrt{2\pi}}\; e^{ - \frac{(x-\mu)^2}{2\sigma^2}}$

Podobnie wzór na skumulowaną funkcję prawdopodobieństwa rozkładu normalnego jest następujący:

$\displaystyle P[X\leq x]=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^x e^{-\frac{(x - \mu)^2}{2\sigma^2}}\, dx ,\quad x\in\mathbb{R}$

Zastosowanie centralnego twierdzenia granicznego polega na tym, że rozkład Poissona może przybliżać rozkład normalny, gdy wartość λ jest wystarczająco duża.

$\text{Poisson}(\lambda)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(\lambda, \sqrt{\lambda}\right)$

Innym zastosowaniem centralnego twierdzenia granicznego jest to, że rozkład dwumianowy można aproksymować rozkładem normalnym dla zbiorów danych z dużą liczbą obserwacji.

$\text{Bin}(n,p)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(n\cdot p, \sqrt{n\cdot p \cdot (1-p)}\right)$

Standardowy rozkład normalny

Standardowy rozkład normalny , zwany także jednostkowym rozkładem normalnym , jest najprostszym przypadkiem rozkładu normalnego. Dokładniej, standardowy rozkład normalny jest rozkładem normalnym o wartościach średniej i odchylenia standardowego równych odpowiednio 0 i 1.

$\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}$

Należy zauważyć, że dowolny rozkład normalny można przekształcić w standardowy rozkład normalny, stosując proces zwany typowaniem, który polega na odjęciu jego średniej arytmetycznej od każdej wartości, a następnie podzieleniu przez jej odchylenie standardowe.

Dodatkowo standardowy rozkład normalny służy do określenia prawdopodobieństwa rozkładu normalnego przy użyciu jego tabeli prawdopodobieństwa. Zatem, aby znaleźć prawdopodobieństwo rozkładu normalnego, najpierw wprowadza się zmienną w celu przekształcenia jej w standardowy rozkład normalny, a następnie sprawdzamy w tabeli, jaka jest odpowiadająca wartość prawdopodobieństwa. Aby dowiedzieć się więcej, kliknij poniższy link:

➤ Zobacz: Standardowy rozkład normalny

Rozkład normalny i reguła empiryczna

W statystyce praktyczna zasada , zwana także regułą 68-95-99,7 , to reguła określająca procent wartości w rozkładzie normalnym mieszczących się w granicach trzech odchyleń standardowych od średniej.

Mówiąc dokładniej, praktyczna zasada stanowi, co następuje:

68% wartości w rozkładzie normalnym mieści się w obrębie jednego odchylenia standardowego średniej.
95% wartości w rozkładzie normalnym mieści się w granicach dwóch odchyleń standardowych od średniej.
99,7% wartości w rozkładzie normalnym mieści się w trzech odchyleniach standardowych od średniej.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej