Jak ręcznie obliczyć r-kwadrat
W statystyce R kwadrat (R 2 ) mierzy część wariancjizmiennej odpowiedzi , którą można wyjaśnić zmienną predykcyjną w modelu regresji.
Do obliczenia R do kwadratu używamy następującego wzoru:
R 2 = [ (nΣxy – (Σx)(Σy)) / (√ nΣx 2 -(Σx) 2 * √ nΣy 2 -(Σy) 2 ) ] 2
Poniższy przykład pokazuje krok po kroku, jak ręcznie obliczyć współczynnik R-kwadrat dla danego modelu regresji.
Krok 1: Utwórz zbiór danych
Najpierw utwórzmy zbiór danych:
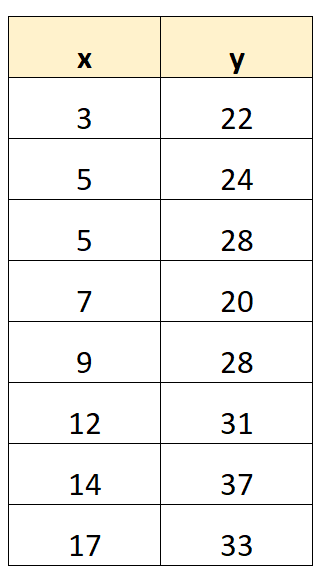
Krok 2: Oblicz niezbędne wskaźniki
Następnie obliczmy każdą metrykę, której potrzebujemy we wzorze R2 :
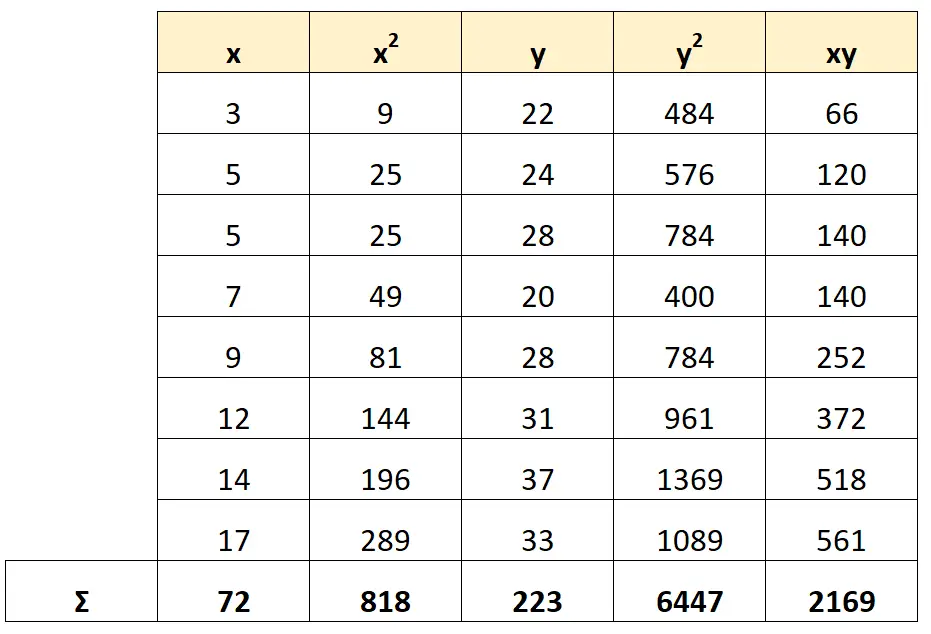
Krok 3: Oblicz R do kwadratu
Na koniec zintegrujemy każdą metrykę ze wzorem na R2 :
- R 2 = [ (nΣxy – (Σx)(Σy)) / (√ nΣx 2 -(Σx) 2 * √ nΣy 2 -(Σy) 2 ) ] 2
- R 2 = [ (8*(2169) – (72)(223)) / (√ 8*(818)-(72) 2 * √ 8*(6447)-(223) 2 ) ] 2
- R2 = 0,6686
Uwaga: n we wzorze reprezentuje liczbę obserwacji w zbiorze danych i w tym przykładzie oznacza n = 8 obserwacji.
Zakładając, że x jest zmienną predykcyjną, a y jest zmienną odpowiedzi w tym modelu regresji, R-kwadrat modelu wynosi 0,6686 .
To mówi nam, że 66,86% zmienności zmiennej y można wyjaśnić zmienną x .
Dodatkowe zasoby
Wprowadzenie do prostej regresji liniowej
Wprowadzenie do wielokrotnej regresji liniowej
R vs R-Square: jaka jest różnica?
Jaka jest dobra wartość R-kwadrat?
o autorze
Dr Benjamin Anderson
Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej