Jak obliczyć wartości p w programie excel (3 przykłady)

W statystyce testujemy hipotezy , aby określić, czy stwierdzenie dotyczące parametru populacji jest prawdziwe, czy nie.

Kiedy przeprowadzamy test hipotez, często otrzymujemy statystykę testu T-score.

Gdy już znajdziemy statystykę testu t-score, możemy znaleźć powiązaną z nią wartość p.

Jeśli ta wartość p jest mniejsza niż pewna wartość (np. 0,10, 0,05, 0,01), wówczas odrzucamy hipotezę zerową testu i stwierdzamy, że nasze wyniki są statystycznie istotne.

Poniższe przykłady pokazują, jak obliczyć wartość p dla statystyki testowej w programie Excel w trzech różnych scenariuszach.

Przykład 1: Oblicz wartość P dla testu dwustronnego

Załóżmy, że botanik chce wiedzieć, czy średnia wysokość określonego gatunku rośliny wynosi 15 cali.

W losowej próbie 12 roślin stwierdziła, że średnia wysokość próbki wynosi 14,33 cala, a odchylenie standardowe próbki wynosi 1,37 cala.

Wykonuje test hipotez przy użyciu następujących hipotez zerowych i alternatywnych:

H ₀ (hipoteza zerowa): μ= 15 cali

_HA (hipoteza alternatywna): μ ≠ 15 cali

Statystykę testową oblicza się w następujący sposób:

• t = ( X – µ) / (s/ √n )
• t = (14,33-15) / (1,37/√ 12 )
• t = -1,694

Stopnie swobody powiązane z tą statystyką testową wynoszą n-1 = 12-1 = 11 .

Aby znaleźć wartość p dla tej statystyki testowej, użyjemy następującej formuły w Excelu:

 =T.DIST.2T(ABS(-1.694), 11)

Poniższy zrzut ekranu pokazuje, jak wykorzystać tę formułę w praktyce.

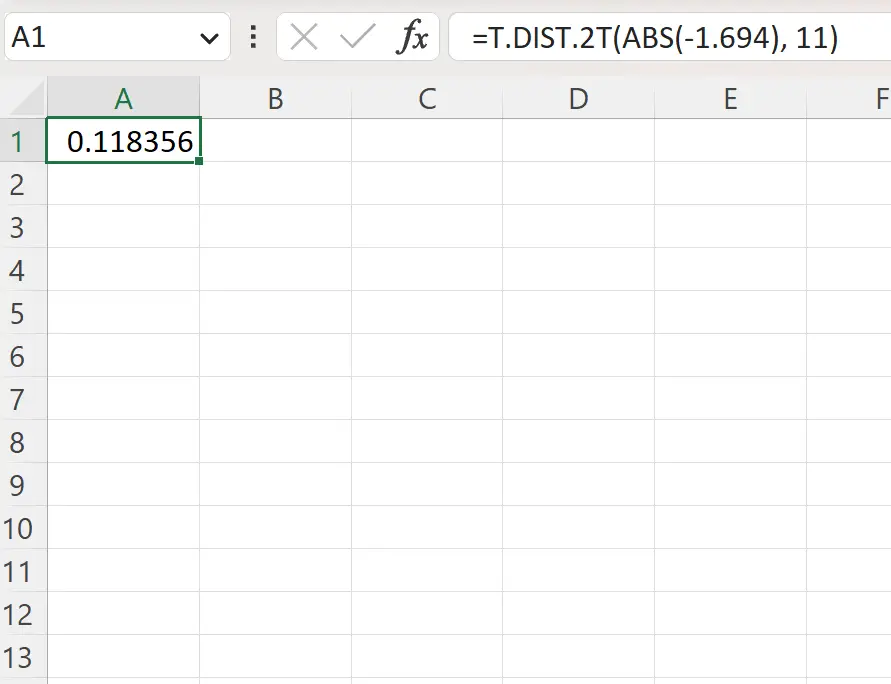
Dwustronna wartość p wynosi 0,1184 .

Od tej wartości jest nie mniejsza niż 0,05, nie odrzucamy hipotezy zerowej. Nie mamy wystarczających dowodów, aby stwierdzić, że średnia wysokość rośliny różni się od 15 cali.

Przykład 2: Oblicz wartość P dla testu po lewej stronie

Załóżmy, że średnia waga pewnego gadżetu produkowanego w fabryce wynosi 20 gramów. Inspektor szacuje jednak, że rzeczywista średnia waga jest mniejsza niż 20 gramów.

Aby to przetestować, waży prostą losową próbkę 20 widżetów i otrzymuje następujące informacje:

• n = 20 widżetów
• x = 19,8 grama
• s = 3,1 grama

Następnie przeprowadza test hipotezy, korzystając z następujących hipotez zerowych i alternatywnych:

H ₀ (hipoteza zerowa): μ ≥ 20 gramów

_HA (hipoteza alternatywna): μ < 20 gramów

Statystykę testową oblicza się w następujący sposób:

• t = ( X – µ) / (s/ √n )
• t = (19,8-20) / (3,1/√ 20 )
• t = -,2885

Stopnie swobody powiązane z tą statystyką testową wynoszą n-1 = 20-1 = 19 .

Aby znaleźć wartość p dla tej statystyki testowej, użyjemy następującej formuły w Excelu:

 =T.DIST(-.2885, 19, TRUE)

Poniższy zrzut ekranu pokazuje, jak wykorzystać tę formułę w praktyce.

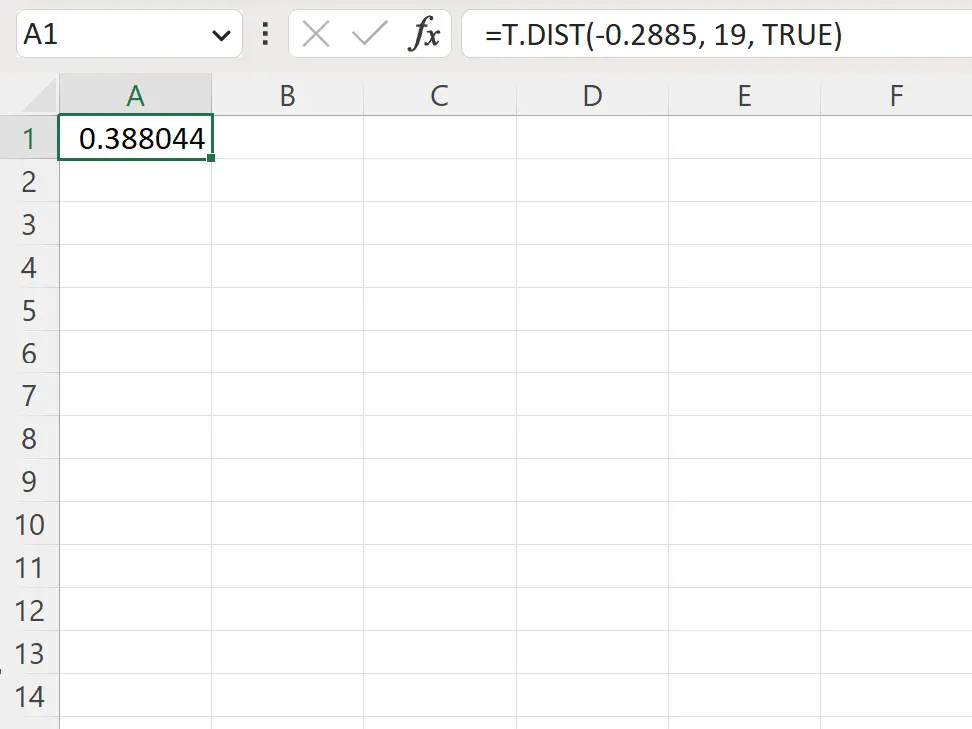
Wartość p po lewej stronie wynosi 0,388044 .

Od tej wartości jest nie mniejsza niż 0,05, inspektor nie odrzuca hipotezy zerowej. Nie ma wystarczających dowodów, aby stwierdzić, że faktyczna średnia waga widżetów produkowanych w tej fabryce wynosi mniej niż 20 gramów.

Uwaga : Użyliśmy argumentu PRAWDA , aby określić, że przy obliczaniu wartości p należy użyć funkcji rozkładu skumulowanego.

Przykład 3: Oblicz wartość P dla testu prawostronnego

Załóżmy, że średnia wysokość określonego gatunku rośliny wynosi 10 cali. Jednak jeden z botaników twierdzi, że prawdziwa średnia wysokość wynosi ponad 10 cali.

Aby sprawdzić to twierdzenie, mierzy wysokość prostej losowej próbki 15 roślin i uzyskuje następujące informacje:

• n = 15 roślin
• x = 11,4 cala
• s = 2,5 cala

Następnie przeprowadza test hipotezy, korzystając z następujących hipotez zerowych i alternatywnych:

H ₀ (hipoteza zerowa): μ ≤ 10 cali

_HA (hipoteza alternatywna): μ > 10 cali

Statystykę testową oblicza się w następujący sposób:

• t = ( X – µ) / (s/ √n )
• t = (11,4-10) / (2,5/√ 15 )
• t = 2,1689

Stopnie swobody powiązane z tą statystyką testową wynoszą n-1 = 15-1 = 14 .

Aby znaleźć wartość p dla tej statystyki testowej, użyjemy następującej formuły w Excelu:

 =T.DIST.RT(2.1689, 14)

Poniższy zrzut ekranu pokazuje, jak wykorzystać tę formułę w praktyce.

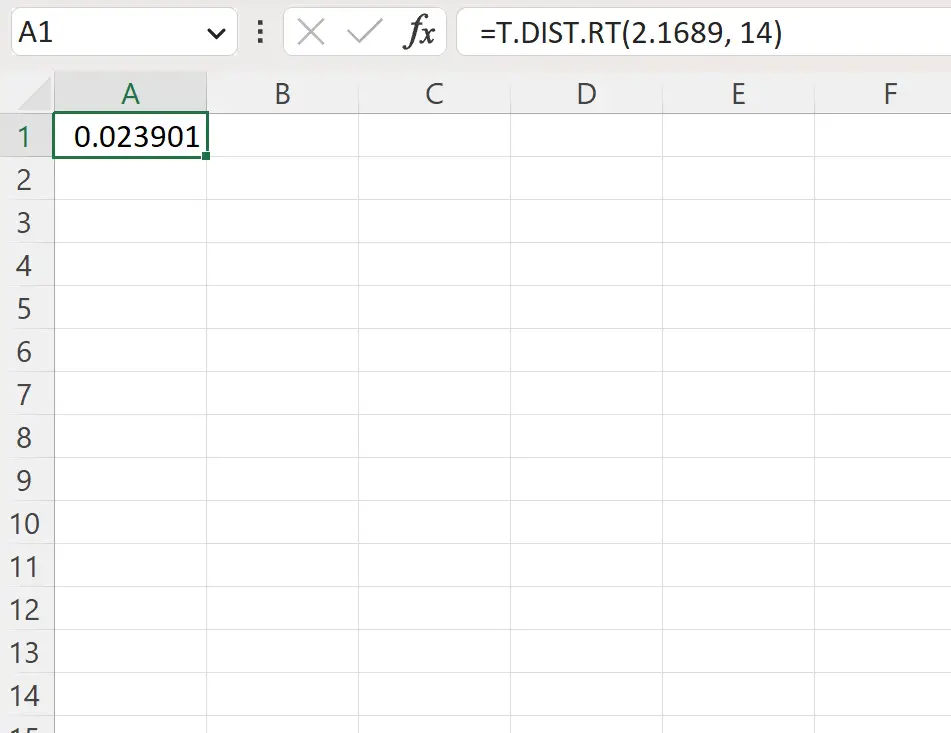
Wartość p po prawej stronie wynosi 0,023901 .

Jeśli wartość ta jest mniejsza niż 0,05, botanik może odrzucić hipotezę zerową. Ma wystarczające dowody, aby stwierdzić, że prawdziwa średnia wysokość tego gatunku roślin wynosi ponad 10 cali.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w programie Excel:

Jak znaleźć wartość P na podstawie wyniku Z w programie Excel
Jak znaleźć wartość P statystyki F w programie Excel
Jak znaleźć wartość P statystyki chi-kwadrat w programie Excel