Odchylenie standardowe w arkuszach google (próba i populacja)

Odchylenie standardowe jest jednym z najczęstszych sposobów pomiaru rozkładu wartości w zbiorze danych.

Istnieją dwa różne typy odchyleń standardowych, które można obliczyć, w zależności od rodzaju danych, z którymi pracujesz.

1. Odchylenie standardowe populacji

Odchylenie standardowe populacji należy obliczyć, gdy zbiór danych, z którym pracujesz, reprezentuje całą populację, czyli każdą wartość, która Cię interesuje.

Wzór na obliczenie odchylenia standardowego populacji, oznaczonego σ, jest następujący:

σ = √ Σ(x _i – μ) ² / N

Złoto:

• Σ : Symbol oznaczający „sumę”
• x _i : i- ^ta wartość w zestawie danych
• μ : średnia populacji
• N : Wielkość populacji

2. Przykład odchylenia standardowego

Należy obliczyć odchylenie standardowe próbki, jeśli zbiór danych, z którym pracujesz, reprezentuje próbkę pobraną z większej populacji będącej przedmiotem zainteresowania.

Wzór na obliczenie odchylenia standardowego próbki, oznaczonego s , jest następujący:

s = √ Σ(x _i – x̄) ² / (n – 1)

Złoto:

• Σ : Symbol oznaczający „sumę”
• x _i : i- ^ta wartość w zestawie danych
• x̄ : Przykładowe środki
• n : Rozmiar próbki

Poniższe przykłady pokazują, jak obliczyć odchylenie standardowe próby i populacji w Arkuszach Google.

Przykład 1: Obliczanie przykładowego odchylenia standardowego w Arkuszach Google

Załóżmy, że biolog chce podsumować odchylenie standardowe masy określonego gatunku żółwia i dlatego pobiera prostą losową próbkę 20 żółwi z populacji.

Ponieważ do oszacowania odchylenia standardowego populacji wykorzystuje próbkę, może obliczyć odchylenie standardowe próbki.

Poniższy zrzut ekranu pokazuje, jak używać funkcji STDEV.S() do obliczenia odchylenia standardowego próbki:

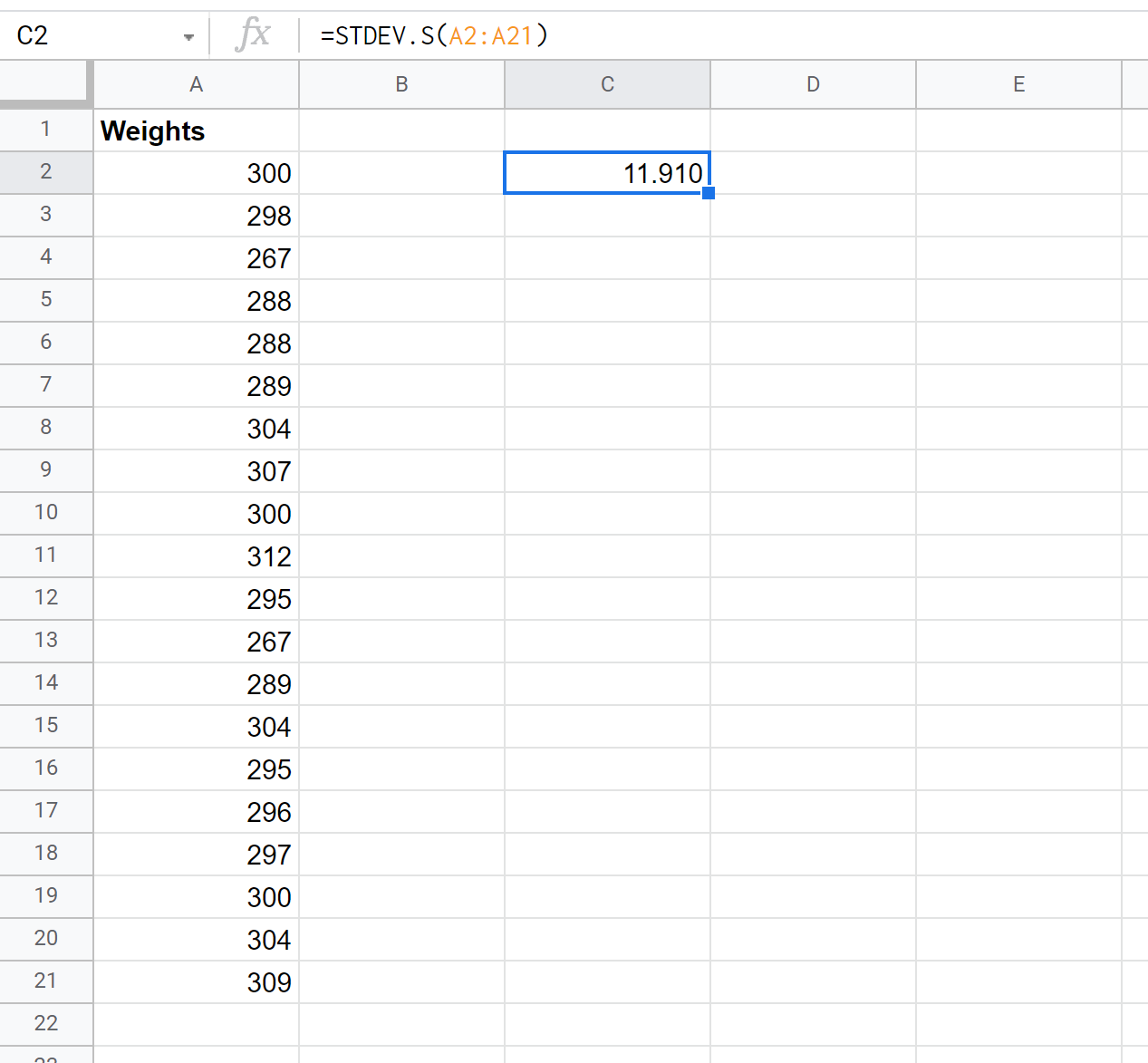
Okazuje się, że odchylenie standardowe próbki wynosi 11,91 .

Należy zauważyć, że funkcja STDEV() zwróci również odchylenie standardowe próbki.

Przykład 2: Obliczanie odchylenia standardowego populacji w Arkuszach Google

Załóżmy, że trener koszykówki chce podsumować odchylenie standardowe punktów zdobytych przez 12 zawodników jego drużyny.

Ponieważ interesują go tylko punkty zdobyte przez jego zawodników, a nie innych graczy z innej drużyny, może obliczyć odchylenie standardowe populacji.

Poniższy zrzut ekranu pokazuje, jak używać funkcji STDEV.P() do obliczania odchylenia standardowego populacji:

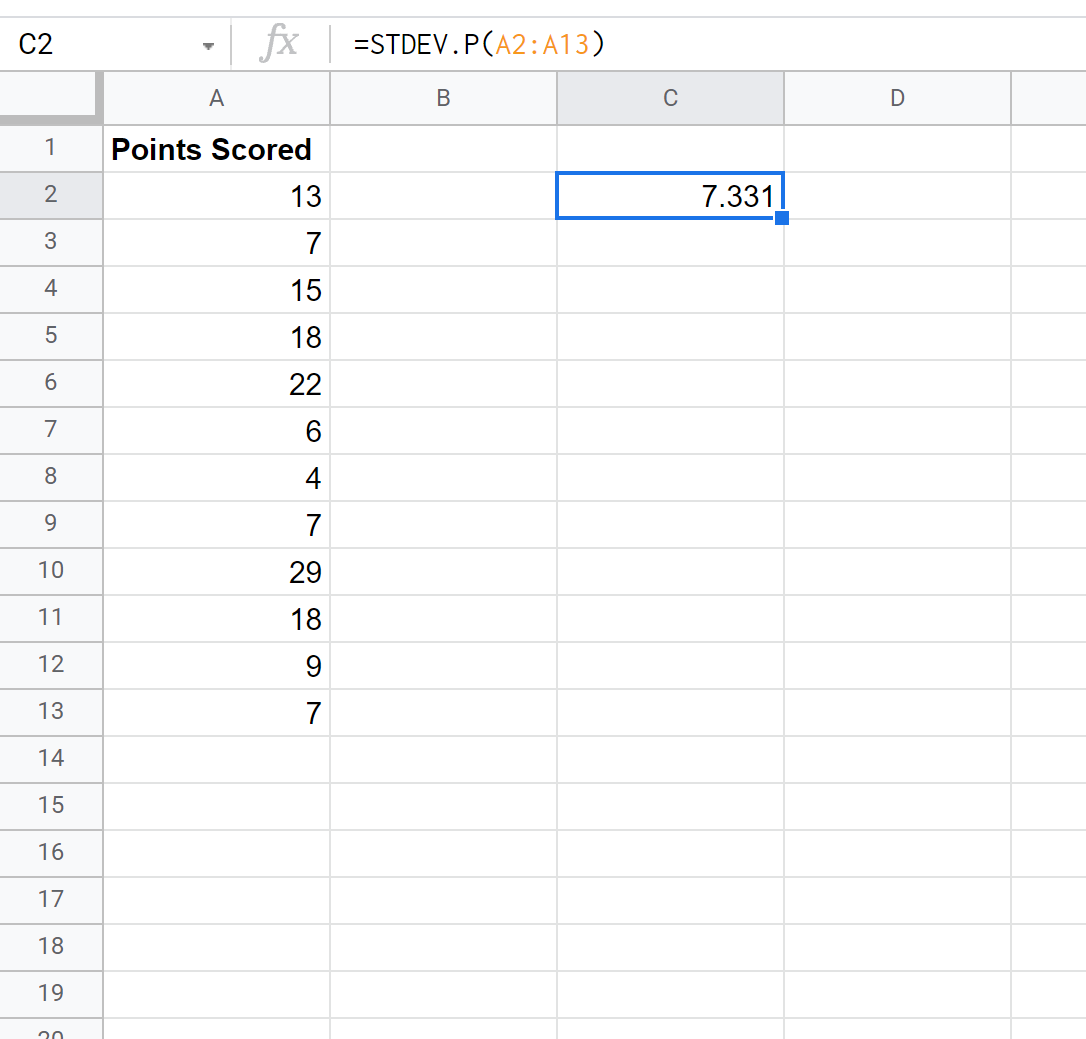
Odchylenie standardowe populacji wynosi 7331 .

Dodatkowe zasoby

Poniższe tutoriale dostarczają dodatkowych informacji na temat odchylenia standardowego:

• Populacja vs. Przykładowe odchylenie standardowe: kiedy używać każdego z nich
• Współczynnik zmienności a odchylenie standardowe: różnica
• Dlaczego odchylenie standardowe jest ważne?

Poniższe samouczki wyjaśniają, jak obliczać inne dane dotyczące spreadów w Arkuszach Google:

• Jak obliczyć rozstęp międzykwartylowy w Arkuszach Google
• Jak obliczyć współczynnik zmienności w Arkuszach Google