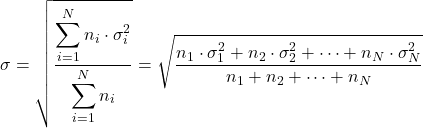Odchylenie standardowe (lub odchylenie standardowe)
W tym artykule wyjaśniono, czym jest odchylenie standardowe, zwane także odchyleniem standardowym. Dowiesz się, jak obliczyć odchylenie standardowe, znajdziesz praktyczny przykład krok po kroku oraz kalkulator online pozwalający znaleźć odchylenie standardowe dowolnej próbki danych.
Co to jest odchylenie standardowe (lub odchylenie standardowe)?
Odchylenie standardowe , zwane także odchyleniem standardowym , jest miarą rozproszenia statystycznego. Inaczej mówiąc, odchylenie standardowe to wartość wskazująca rozproszenie zbioru danych statystycznych.
Dlatego odchylenie standardowe (lub odchylenie standardowe) służy do ilościowego określenia rozproszenia populacji lub próby statystycznej. Im większe odchylenie standardowe serii danych, tym bardziej rozproszone są dane. Interpretacji można dokonać także w drugą stronę, jeśli odchylenie standardowe jest niskie, oznacza to, że ogólnie dane są bardzo zbliżone do średniej.
Przy obliczaniu odchylenia standardowego lub typowego w populacji symbolem odchylenia standardowego jest grecka litera sigma (σ). Ale jeśli chodzi o odchylenie standardowe próbki, litera s służy do przedstawienia pomiaru statystycznego.
W niektórych księgach statystycznych i prawdopodobieństwie odchylenie standardowe nazywane jest również odchyleniem standardowym.
Wzór na odchylenie standardowe (lub odchylenie standardowe).
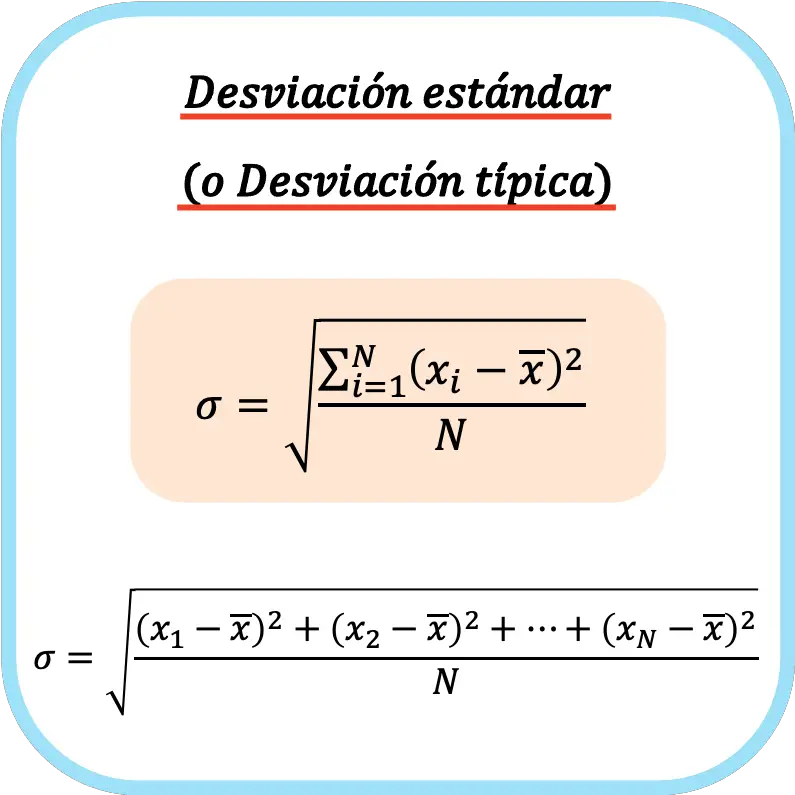
Odchylenie standardowe (lub odchylenie standardowe) jest równe pierwiastkowi kwadratowemu z sumy kwadratów odchyleń serii danych podzielonej przez całkowitą liczbę obserwacji.
Wzór na obliczenie odchylenia standardowego (lub odchylenia standardowego) jest zatem następujący:
👉 Możesz skorzystać z poniższego kalkulatora, aby obliczyć odchylenie standardowe dowolnego zbioru danych.
Podsumowując, aby znaleźć odchylenie standardowe zbioru danych, należy obliczyć wszystkie odchylenia (zdefiniowane jako różnica między punktem danych a średnią arytmetyczną), zwiększyć odchylenia do dwóch, dodać je wszystkie, a następnie podzielić przez całkowity. liczbę danych i na koniec weź pierwiastek kwadratowy.
Przykład odchylenia standardowego (lub odchylenia standardowego)
Biorąc pod uwagę definicję odchylenia standardowego (lub odchylenia typowego), poniżej znajduje się przykład krok po kroku, dzięki któremu można zobaczyć, jak obliczane jest odchylenie standardowe serii danych.
- Oblicz odchylenie standardowe następujących wartości: 3, 6, 2, 9, 4.
Pierwszą rzeczą, którą musimy zrobić, to określić średnią próbki. Aby to zrobić, sumujemy wszystkie dane i dzielimy przez całkowitą liczbę obserwacji, która wynosi pięć:
![]()
Korzystamy teraz ze wzoru na odchylenie standardowe:

Podstawiamy dane do wzoru:
![]()
Na koniec obliczamy odchylenie standardowe:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle\sigma & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{5}}\\[2ex]&= \sqrt{\frac{30,8}{5}}=\sqrt{6,16}=2,48 \end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d52b5396ff383310226cf152a9bf87ea_l3.png)
Kalkulator odchylenia standardowego (lub odchylenia standardowego).
Wprowadź zestaw danych statystycznych do poniższego kalkulatora online, aby obliczyć jego odchylenie standardowe (lub odchylenie standardowe). Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego.
Odchylenie standardowe (lub typowe) dla pogrupowanych danych
Aby obliczyć odchylenie standardowe (lub odchylenie standardowe) danych pogrupowanych w przedziały , należy wykonać następujące kroki:
- Znajdź średnią zgrupowanych danych.
- Oblicz odchylenia zgrupowanych danych.
- Wyrównaj każdą szczelinę.
- Pomnóż każdy poprzedni wynik przez częstotliwość jego przedziału.
- Dodaj sumę wszystkich wartości uzyskanych w poprzednim kroku.
- Podziel przez całkowitą liczbę obserwacji.
- Weź pierwiastek kwadratowy z poprzedniej wartości. Wynikowa liczba jest odchyleniem standardowym pogrupowanych danych.
Podsumowując, wzór na obliczenie odchylenia standardowego danych pogrupowanych w przedziały jest następujący:
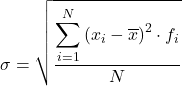
Chociaż zwykle stosuje się powyższy wzór, można również zastosować następujące wyrażenie algebraiczne, ponieważ uzyskuje się ten sam wynik:
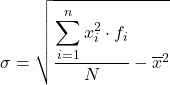
Aby zobaczyć, jak to się robi, poniżej znajduje się ćwiczenie krok po kroku dotyczące odchylenia standardowego danych pogrupowanych w przedziały. Dokładniej, zostanie obliczone odchylenie standardowe następujących danych statystycznych:
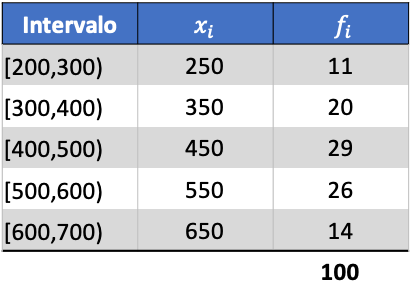
Najpierw mnożymy wynik klasowy każdego przedziału przez jego częstotliwość, aby obliczyć średnią arytmetyczną:
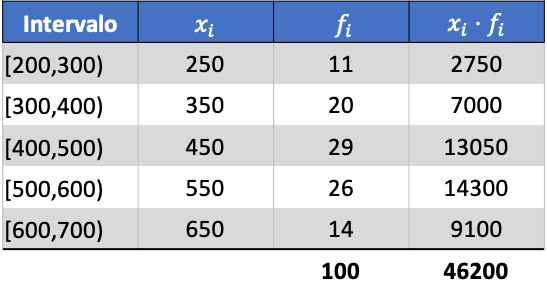
Zatem średnia z pogrupowanych danych będzie wynosić:
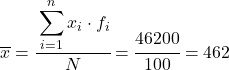
Teraz, gdy znamy wartość średniej, musimy dodać do tabeli danych następujące trzy kolumny:
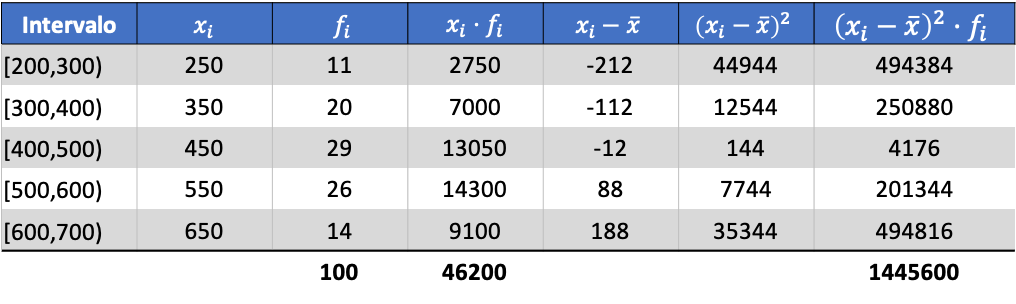
Wtedy odchylenie standardowe zgrupowanych danych będzie wynikiem pierwiastka kwadratowego sumy z ostatniej kolumny podzielonej przez całkowitą liczbę obserwacji:
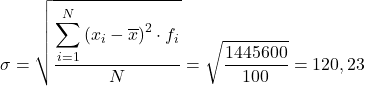
Standardowe (lub typowe) odchylenie i wariancja
Zależność między odchyleniem standardowym (lub odchyleniem typowym) a wariancją polega na tym, że odchylenie standardowe jest pierwiastkiem kwadratowym wariancji.
Jeśli więc znamy wartość wariancji zbioru danych, możemy łatwo obliczyć odchylenie standardowe, biorąc pierwiastek kwadratowy. Lub odwrotnie, jeśli znamy odchylenie standardowe, możemy znaleźć wariancję, podnosząc wartość do kwadratu.
![]()
W rzeczywistości wariancję można przedstawić po prostu za pomocą kwadratowego symbolu odchylenia standardowego. Zatem symbol wariancji populacji to sigma kwadrat (σ 2 ), a symbol wariancji próbki to kwadrat (s 2 ).
Dodatkowo, pojęcia odchylenia standardowego i wariancji mają podobną interpretację, ponieważ oba pokazują rozproszenie szeregu danych statystycznych.
Właściwości odchylenia standardowego (lub odchylenia standardowego)
Odchylenie standardowe ma następujące właściwości:
- Odchylenie standardowe próbki danych nie może być ujemne.
![]()
- Odchylenie standardowe wyniesie zero, jeśli wszystkie dane są takie same.
![]()
- Jeśli do wszystkich danych zostanie dodany składnik stały, wartość odchylenia standardowego nie ulegnie zmianie.
![]()
- Jeśli wszystkie dane zostaną pomnożone przez liczbę, odchylenie standardowe zostanie pomnożone przez wartość bezwzględną tej liczby.
![]()
- Odchylenie standardowe sumy dwóch zmiennych losowych jest równe pierwiastkowi kwadratowemu sumy wariancji zmiennych plus dwukrotność kowariancji między dwiema zmiennymi.
![]()
- Jeśli znamy odchylenia standardowe różnych rozkładów (σ i ) i liczbę danych (n i ), możemy obliczyć całkowite odchylenie standardowe, stosując następujący wzór: