Odchylenie standardowe próbki (lub odchylenie standardowe próbki)
W tym artykule wyjaśniono, czym jest odchylenie standardowe próbki w statystyce. Dowiesz się również, jak obliczyć odchylenie standardowe próby, jakie jest rozwiązane ćwiczenie i jaka jest różnica między odchyleniem standardowym próbki a odchyleniem standardowym populacji. Wreszcie możesz obliczyć odchylenie standardowe dowolnej próbki za pomocą kalkulatora online.
Jakie jest odchylenie standardowe próbki?
Odchylenie standardowe próbki (lub odchylenie standardowe próbki ) jest miarą rozproszenia, która wskazuje zmienność próbki. Dokładniej, odchylenie standardowe próbki jest równe pierwiastkowi kwadratowemu z sumy kwadratów odchyleń podzielonej przez wielkość próby minus jeden.
Symbolem odchylenia standardowego próbki jest mała litera s .
Odchylenie standardowe próbki jest czasami nazywane odchyleniem quasi-standardowym (lub odchyleniem quasi-standardowym), aby odróżnić je od odchylenia standardowego populacji. Poniżej zobaczymy, jak odchylenie standardowe próby różni się od odchylenia standardowego populacji.
Przykład wzoru na odchylenie standardowe
Odchylenie standardowe próbki jest równe pierwiastkowi kwadratowemu z sumy kwadratów odchyleń danych próbki podzielonej przez wielkość próby minus jeden. Zatem wzór na obliczenie odchylenia standardowego próbki jest następujący:

Złoto:
-

jest odchyleniem standardowym próbki (lub odchyleniem standardowym próbki).
-

jest wartością danych

.
-

to wielkość próbki
-

to przykładowe środki.
👉 Możesz skorzystać z poniższego kalkulatora, aby obliczyć odchylenie standardowe dowolnej próbki danych.
Przykład obliczenia odchylenia standardowego próbki
Teraz, gdy znamy definicję odchylenia standardowego próbki (lub odchylenia standardowego próbki) i jaki jest jego wzór, rozwiążemy prosty przykład, aby zakończyć zrozumienie sposobu jego obliczania.
- Firma obuwnicza prowadzi badania rynku, aby podjąć decyzję o wprowadzeniu na rynek nowego modelu obuwia. Ponieważ istnieje wiele różnych modeli, a Ty chcesz po prostu przeprowadzić szybką wstępną analizę, decydujesz się po prostu spojrzeć na cenę próbki pięciu najlepszych konkurencyjnych marek obuwia (ceny pokazano poniżej). Jakie jest odchylenie standardowe tego zbioru danych?
98 € 70 € 125 € 89 € 75 €
Aby obliczyć odchylenie standardowe próbki, najpierw musimy obliczyć średnią próbki :
![]()
Po obliczeniu średniej próbki stosujemy wzór na odchylenie standardowe próbki:
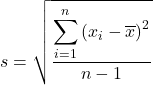
Podstawiamy przykładowe dane do wzoru:
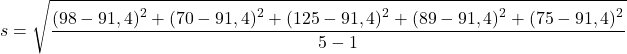
Pozostaje zatem rozwiązać operacje pozwalające obliczyć odchylenie standardowe próbki:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s&=\sqrt{\frac{6,6^2+(-21,4)^2+33,6^2+(-2,4)^2+(-16,4)^2}{4}}\\[2ex]\displaystyle s&=\sqrt{\frac{43,56+457,96+1128,96+5,76+268,96}{4}}\\[2ex]s&=\sqrt{\frac{1905,2}{4}}\\[2ex]s&=\sqrt{476,3}\\[2ex]s&=21,82 \end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0a9a5050ca14179085932bb9cc550ebb_l3.png)
Różnica w próbie analizowanej próby wynosi zatem 21,82 EUR.
Odchylenie standardowe próbki i odchylenie standardowe populacji
Następnie zobaczymy, jakie są różnice między odchyleniem standardowym próby a odchyleniem standardowym populacji, ponieważ są to dwa powiązane pojęcia statystyczne, co do których musimy mieć jasność.
W estadística odchylenie standardowe populacji to odchylenie standardowe uzyskane podczas obliczeń ze wszystkimi elementami populacji, chociaż odchylenie standardowe to odchylenie standardowe uzyskane w wyniku przeprowadzenia obliczeń tylko z jednym przykładem danych z populacji .
Matematycznie różnica między odchyleniem standardowym próby a odchyleniem standardowym populacji jest mianownikiem wzoru użytego do jej obliczenia. Aby obliczyć odchylenie standardowe próbki, należy je podzielić przez n-1, natomiast odchylenie standardowe populacji oblicza się, dzieląc przez n.
Dodatkowo, aby odróżnić odchylenie standardowe próby od odchylenia standardowego populacji, są one oznaczone różnymi symbolami. Symbolem odchylenia standardowego próby jest litera s, natomiast symbolem odchylenia standardowego populacji jest grecka litera σ.
Ogólnie rzecz biorąc, nie wszystkie elementy populacji są znane, dlatego badanie statystyczne przeprowadza się na próbie populacji. Zatem odchylenie standardowe próbki służy do punktowego oszacowania wartości odchylenia standardowego całej populacji.
Przykład kalkulatora odchylenia standardowego
Wprowadź dane próbki do poniższego kalkulatora online, aby obliczyć odchylenie standardowe próbki (lub odchylenie standardowe próbki). Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego.