Jak interpretować odchylenie standardowe równe zero

W statystyce odchylenie standardowe służy do pomiaru rozkładu wartości w próbie.

Do obliczenia odchylenia standardowego danej próbki możemy posłużyć się następującym wzorem:

√ Σ(x _i – x _bar ) ² / (n-1)

Złoto:

• Σ: Symbol oznaczający „sumę”
• x _i : ^i-ta wartość próbki
• x _słupek : Oznacza próbkę
• n: Wielkość próbki

Im wyższa wartość odchylenia standardowego, tym bardziej rozproszone są wartości w próbce .

Im niższa wartość odchylenia standardowego, tym bliżej wartości są pogrupowane.

Jeśli odchylenie standardowe próbki wynosi zero, oznacza to, że wszystkie wartości w próbce są dokładnie takie same.

Innymi słowy, nie ma luki pomiędzy wartościami.

Poniższy przykład pokazuje, jak w praktyce interpretować odchylenie standardowe równe zero.

Przykład: Jak interpretować odchylenie standardowe równe zero

Załóżmy, że zbieramy prostą losową próbkę 10 jaszczurek i mierzymy ich długość (w calach):

Długości : 7, 7, 7, 7, 7, 7, 7, 7, 7, 7

Średnia długość jaszczurek w próbie wynosi 7 cali.

Wiedząc o tym, możemy obliczyć odchylenie standardowe próbki dla tego zbioru danych:

• s = √ Σ(x _i – x _bar ) ² / (n-1)
• s = √ ((7 – 7) ² + (7 – 7) ² + (7 – 7) ² + … + (7 – 7) ² / (10-1)
• s = √ 0 ² + 0 ² + 0 ² + … + 0 ² / 9
• s = 0

Okazuje się, że odchylenie standardowe próbki wynosi 0 .

Ponieważ każda jaszczurka ma dokładnie tę samą długość, rozkład wartości w zbiorze danych wynosi dokładnie zero.

Czy w prawdziwym świecie odchylenie standardowe będzie kiedykolwiek wynosić zero?

Jest całkowicie możliwe, że zbiór danych ze świata rzeczywistego będzie miał odchylenie standardowe równe zero, ale jest to rzadkie.

Najbardziej prawdopodobnym scenariuszem, w którym możesz napotkać odchylenie standardowe równe zero, jest zbieranie małych próbek w przypadku rzadkich zdarzeń.

Załóżmy na przykład, że zbierasz dane o liczbie wypadków drogowych w ciągu jednego tygodnia w określonym mieście.

Jest całkowicie możliwe, że zbierasz następujące dane:

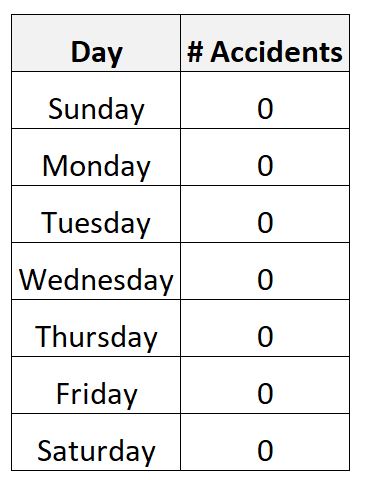
W tym scenariuszu średnia liczba codziennych wypadków wyniosłaby zero, a odchylenie standardowe również wyniosłoby zero.

A może zbierasz następujące dane dotyczące miesięcznej sprzedaży drogiego produktu dla firmy w okresie 6 miesięcy:

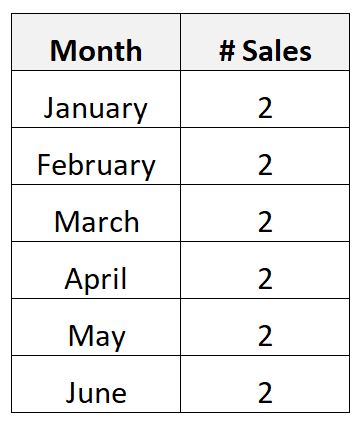
Ponieważ produkt jest tak drogi, okazuje się, że firma sprzedaje tylko dokładnie dwa sztuki miesięcznie.

W tym scenariuszu średnia liczba sprzedawanych produktów w miesiącu wynosi dwa, a odchylenie standardowe miesięcznych sprzedaży produktów wynosi zero.

Ilekroć w prawdziwym zbiorze danych napotkasz odchylenie standardowe równe zero, wiedz, że oznacza to, że każda wartość w zbiorze danych jest dokładnie taka sama.

Dodatkowe zasoby

Poniższe tutoriale dostarczają dodatkowych informacji na temat odchylenia standardowego w statystykach:

Dlaczego odchylenie standardowe jest ważne?
Odchylenie standardowe i błąd standardowy: jaka jest różnica?
Odchylenie standardowe i rozstęp międzykwartylowy: jaka jest różnica?