Odchylenie standardowe i błąd standardowy: jaka jest różnica?

Dwa terminy, które uczniowie często mylą w statystyce, to odchylenie standardowe i błąd standardowy .

Odchylenie standardowe mierzy rozkład wartości w zbiorze danych.

Błąd standardowy to odchylenie standardowe średniej powtarzanych próbek z populacji.

Spójrzmy na przykład, który jasno zilustruje tę ideę.

Przykład: odchylenie standardowe a błąd standardowy

Załóżmy, że mierzymy wagę 10 różnych żółwi.

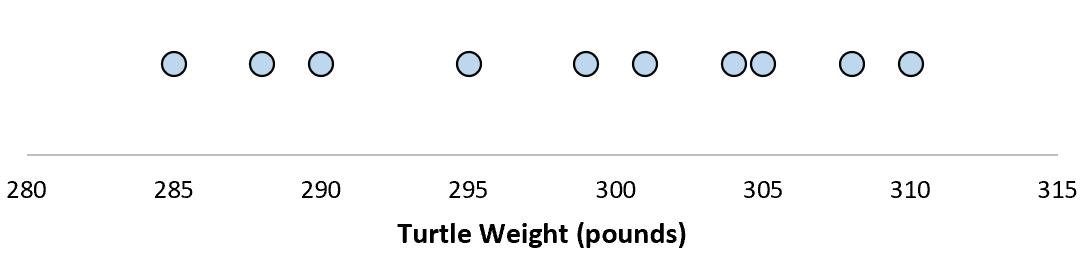
Dla tej próbki składającej się z 10 żółwi możemy obliczyć średnią próbki i odchylenie standardowe próbki:

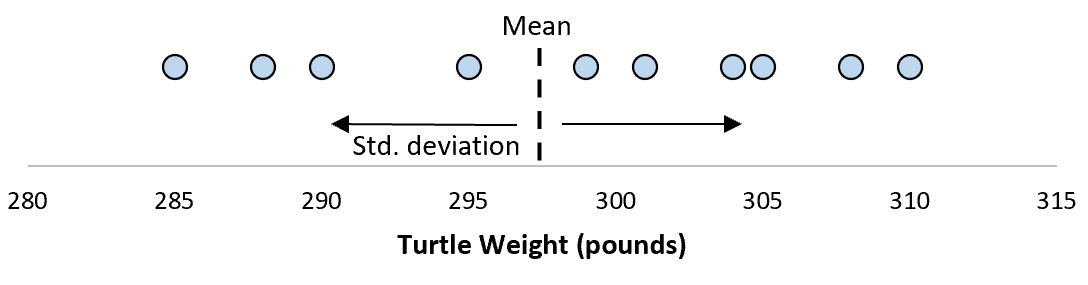
Załóżmy, że odchylenie standardowe wynosi 8,68. Daje nam to wyobrażenie o rozkładzie masy tych żółwi.

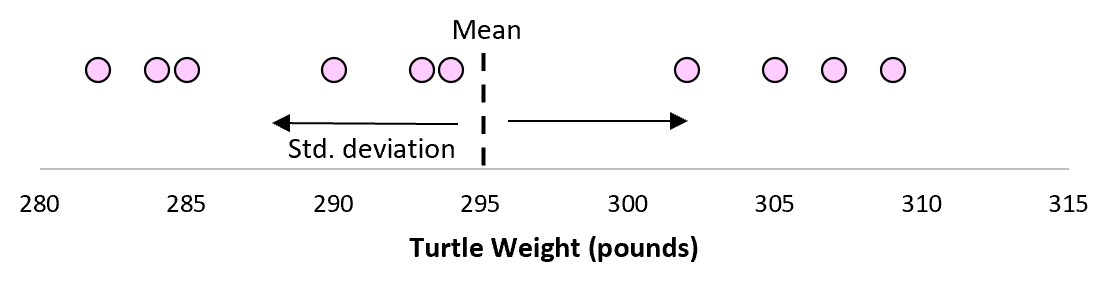
Załóżmy jednak, że zbierzemy inną prostą losową próbkę 10 żółwi i dokonamy również ich pomiarów.

Jest więcej niż prawdopodobne, że ta próbka 10 żółwi będzie miała nieco inną średnią i odchylenie standardowe, mimo że pochodzą z tej samej populacji:

Teraz, jeśli wyobrazimy sobie, że pobieramy powtarzające się próbki z tej samej populacji i rejestrujemy średnią próbki i odchylenie standardowe próbki dla każdej próbki:

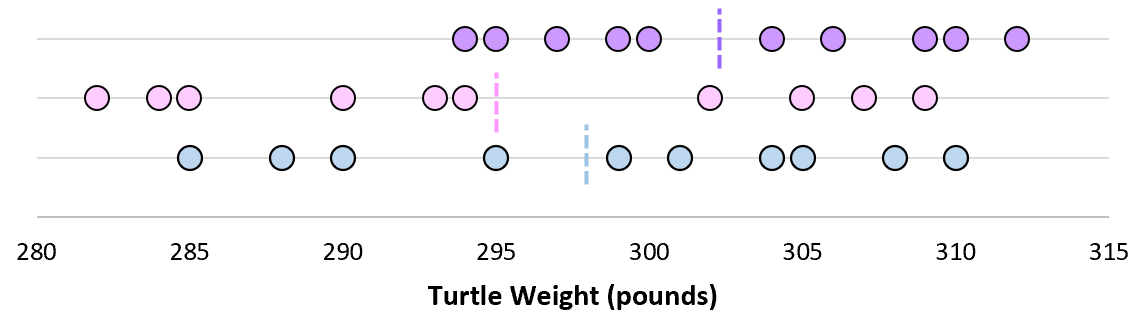
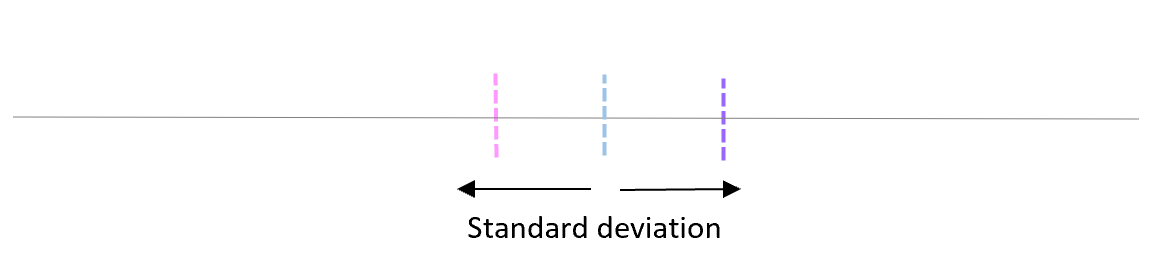
Teraz wyobraź sobie, że nanosimy każdą średnią z próbki na tę samą linię:

Odchylenie standardowe tych średnich nazywa się błędem standardowym.

Wzór na faktyczne obliczenie błędu standardowego jest następujący:

Błąd standardowy = s/ √ n

Złoto:

• s: odchylenie standardowe próbki
• n: wielkość próbki

Jaki jest sens używania błędu standardowego?

Kiedy obliczamy średnią danej próby, w rzeczywistości nie chcemy poznać średniej tej konkretnej próby, ale raczej średnią większej populacji, z której pochodzi próbka.

Posługujemy się jednak próbami, ponieważ o wiele łatwiej jest zebrać dla nich dane niż dla całej populacji.

I oczywiście średnia próbki różni się w zależności od próbki, dlatego używamy błędu standardowego średniej jako sposobu pomiaru precyzji naszego oszacowania średniej.

We wzorze na obliczenie błędu standardowego zauważysz, że wraz ze wzrostem liczebności próby (n) błąd standardowy maleje:

Błąd standardowy = s/ √ n

Powinno to mieć sens, ponieważ większe próbki zmniejszają zmienność i zwiększają szansę, że średnia z naszej próbki będzie bliższa prawdziwej średniej populacji.

Kiedy stosować odchylenie standardowe a kiedy błąd standardowy

Jeśli chcemy po prostu zmierzyć rozkład wartości w zbiorze danych, możemy skorzystać z odchylenia standardowego .

Jeśli jednak chcemy określić ilościowo niepewność wokół oszacowania średniej, możemy skorzystać z błędu standardowego średniej .

W zależności od konkretnego scenariusza i tego, co próbujesz osiągnąć, możesz wybrać odchylenie standardowe lub błąd standardowy.