Odwrotny rozkład normalny: definicja i przykład

Termin odwrotny rozkład normalny odnosi się do metody wykorzystania znanego prawdopodobieństwa do znalezienia odpowiedniej wartości krytycznej z w rozkładzie normalnym .

Nie należy tego mylić z odwrotnym rozkładem Gaussa , który jest ciągłym rozkładem prawdopodobieństwa.

W tym samouczku przedstawiono kilka przykładów wykorzystania odwrotnego rozkładu normalnego w różnych programach statystycznych.

Odwrotny rozkład normalny mamy kalkulator TI-83 lub TI-84

Najprawdopodobniej spotkasz się z terminem „odwrotny rozkład normalny” w kalkulatorze TI-83 lub TI-84, który wykorzystuje następującą funkcję do znalezienia krytycznej wartości z odpowiadającej określonemu prawdopodobieństwu:

invNorm(prawdopodobieństwo, μ, σ)

Złoto:

• prawdopodobieństwo: poziom istotności
• μ: średnia populacji
• σ: odchylenie standardowe populacji

Możesz uzyskać dostęp do tej funkcji w kalkulatorze TI-84, naciskając 2nd, a następnie naciskając vars . Spowoduje to przejście do ekranu DISTR , na którym możesz użyć invNorm() :

Na przykład możemy użyć tej funkcji, aby znaleźć wartość krytyczną z, która odpowiada wartości prawdopodobieństwa wynoszącej 0,05:

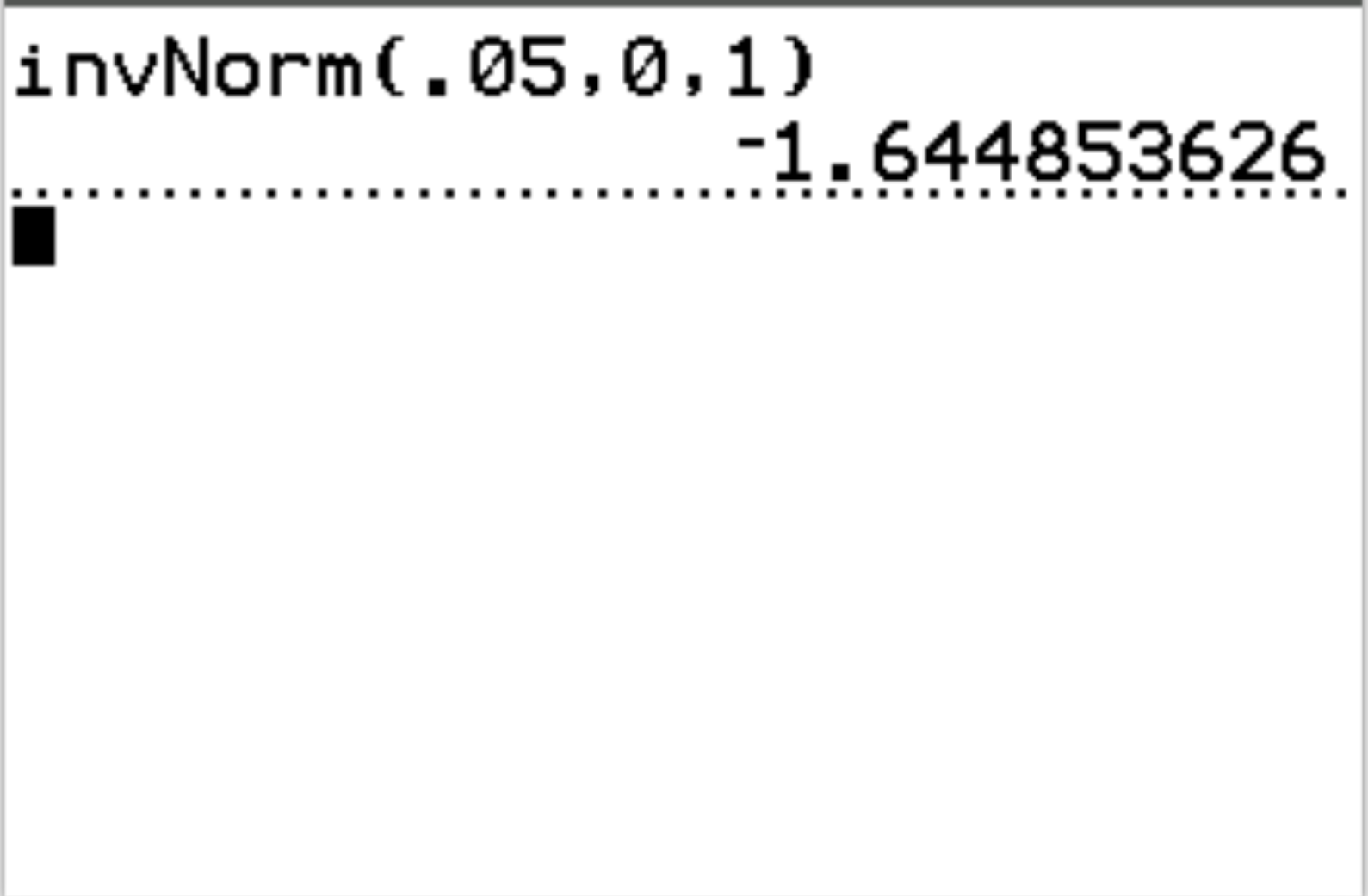
Krytyczna wartość z odpowiadająca wartości prawdopodobieństwa wynoszącej 0,05 wynosi -1,64485 .

Powiązane: Jak używać invNorm na kalkulatorze TI-84 (z przykładami)

Odwrotny rozkład normalny w programie Excel

Aby znaleźć wartość krytyczną z powiązaną z określoną wartością prawdopodobieństwa w programie Excel, możemy użyć funkcji INVNORM() , która wykorzystuje następującą składnię:

INVNORM(p, średnia, sd)

Złoto:

• p: poziom istotności
• średnia: średnia populacji
• sd: odchylenie standardowe populacji

Na przykład możemy użyć tej funkcji, aby znaleźć wartość krytyczną z, która odpowiada wartości prawdopodobieństwa wynoszącej 0,05:

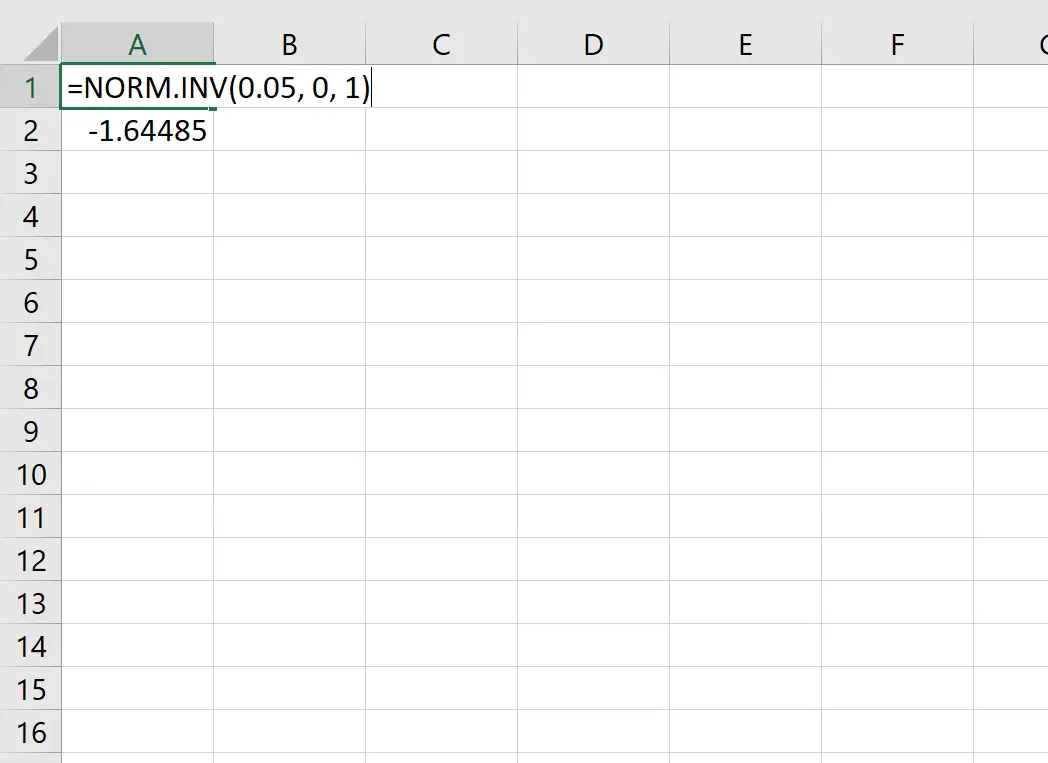
Krytyczna wartość z odpowiadająca wartości prawdopodobieństwa wynoszącej 0,05 wynosi -1,64485 .

Odwrotny rozkład normalny w R

Aby znaleźć wartość krytyczną z powiązaną z określoną wartością prawdopodobieństwa w R, możemy użyć funkcji qnorm() , która wykorzystuje następującą składnię:

qnorm (p, średnia, sd)

Złoto:

• p: poziom istotności
• średnia: średnia populacji
• sd: odchylenie standardowe populacji

Na przykład możemy użyć tej funkcji, aby znaleźć wartość krytyczną z, która odpowiada wartości prawdopodobieństwa wynoszącej 0,05:

 qnorm (p= .05 , mean= 0 , sd= 1 )

[1] -1.644854

Ponownie, krytyczna wartość z odpowiadająca wartości prawdopodobieństwa 0,05 wynosi -1,64485 .