Jak wykonać regresję ols w pythonie (z przykładem)

Regresja metodą najmniejszych kwadratów (OLS) to metoda, która pozwala znaleźć linię najlepiej opisującą związek między jedną lub większą liczbą zmiennych predykcyjnych azmienną odpowiedzi .

Metoda ta pozwala nam znaleźć następujące równanie:

ŷ = b ₀ + b ₁ x

Złoto:

• ŷ : Szacowana wartość odpowiedzi
• b ₀ : Początek linii regresji
• b ₁ : Nachylenie linii regresji

Równanie to może pomóc nam zrozumieć związek między predyktorem a zmienną odpowiedzi, a także można go wykorzystać do przewidzenia wartości zmiennej odpowiedzi, biorąc pod uwagę wartość zmiennej predykcyjnej.

Poniższy przykład krok po kroku pokazuje, jak przeprowadzić regresję OLS w Pythonie.

Krok 1: Utwórz dane

Na potrzeby tego przykładu utworzymy zbiór danych zawierający dwie zmienne dla 15 uczniów:

• Łączna liczba przepracowanych godzin
• Wynik egazminu

Przeprowadzimy regresję OLS, wykorzystując godziny jako zmienną predykcyjną i wynik egzaminu jako zmienną odpowiedzi.

Poniższy kod pokazuje, jak utworzyć ten fałszywy zbiór danych w pandach:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})

#view DataFrame
print (df)

    hours score
0 1 64
1 2 66
2 4 76
3 5 73
4 5 74
5 6 81
6 6 83
7 7 82
8 8 80
9 10 88
10 11 84
11 11 82
12 12 91
13 12 93
14 14 89

Krok 2: Wykonaj regresję OLS

Następnie możemy użyć funkcji modułu statsmodels do przeprowadzenia regresji OLS, używając godzin jako zmiennej predykcyjnej i wyniku jako zmiennej odpowiedzi :

 import statsmodels.api as sm

#define predictor and response variables
y = df[' score ']
x = df[' hours ']

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Fri, 26 Aug 2022 Prob (F-statistic): 2.25e-06
Time: 10:42:24 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================

Z kolumny coef możemy zobaczyć współczynniki regresji i zapisać następujące dopasowane równanie regresji:

Wynik = 65,334 + 1,9824*(godziny)

Oznacza to, że każda dodatkowa godzina nauki wiąże się ze średnim wzrostem wyniku z egzaminu o 1,9824 pkt.

Oryginalna wartość 65 334 mówi nam o średnim oczekiwanym wyniku egzaminu dla studenta studiującego przez zero godzin.

Możemy również użyć tego równania, aby znaleźć oczekiwany wynik egzaminu na podstawie liczby godzin spędzonych przez studenta.

Przykładowo student studiujący 10 godzin powinien uzyskać na egzaminie wynik 85,158 :

Wynik = 65,334 + 1,9824*(10) = 85,158

Oto jak zinterpretować pozostałą część podsumowania modelu:

• P(>|t|): Jest to wartość p powiązana ze współczynnikami modelu. Ponieważ wartość p dla godzin (0,000) jest mniejsza niż 0,05, możemy powiedzieć, że istnieje statystycznie istotny związek pomiędzy godzinami a wynikiem .
• R-kwadrat: mówi nam, że procent zróżnicowania wyników egzaminu można wyjaśnić liczbą godzin nauki. W tym przypadku 83,1% różnic w wynikach można wyjaśnić liczbą przepracowanych godzin.
• Statystyka F i wartość p: Statystyka F ( 63,91 ) i odpowiadająca jej wartość p ( 2,25e-06 ) mówią nam o ogólnym znaczeniu modelu regresji, tj. czy zmienne predykcyjne w modelu są przydatne w wyjaśnianiu zmienności. w zmiennej odpowiedzi. Ponieważ wartość p w tym przykładzie jest mniejsza niż 0,05, nasz model jest istotny statystycznie i godziny uważa się za przydatne do wyjaśnienia zmienności wyniku .

Krok 3: Wizualizuj najlepiej dopasowaną linię

Na koniec możemy użyć pakietu do wizualizacji danych matplotlib , aby zwizualizować linię regresji dopasowaną do rzeczywistych punktów danych:

 import matplotlib. pyplot as plt

#find line of best fit
a, b = np. polyfit (df[' hours '], df[' score '], 1 )

#add points to plot
plt. scatter (df[' hours '], df[' score '], color=' purple ')

#add line of best fit to plot
plt. plot (df[' hours '], a*df[' hours ']+b)

#add fitted regression equation to plot
plt. text ( 1 , 90 , 'y = ' + '{:.3f}'.format(b) + ' + {:.3f}'.format(a) + 'x', size= 12 )

#add axis labels
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

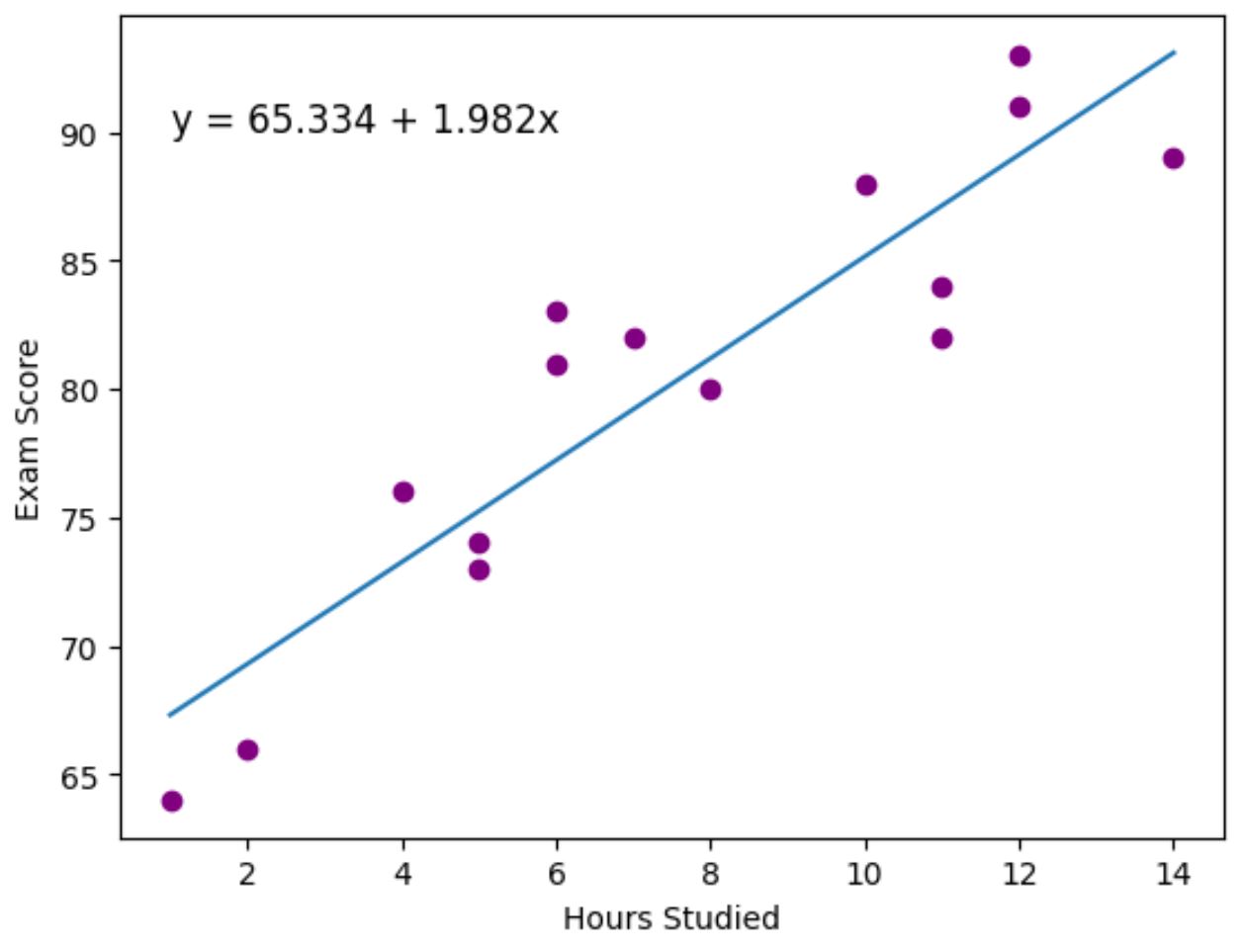
Fioletowe kropki reprezentują rzeczywiste punkty danych, a niebieska linia przedstawia dopasowaną linię regresji.

Użyliśmy także funkcji plt.text() , aby dodać dopasowane równanie regresji do lewego górnego rogu wykresu.

Patrząc na wykres, wydaje się, że dopasowana linia regresji dość dobrze oddaje związek pomiędzy zmienną godzin i zmienną wyniku .

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w Pythonie:

Jak przeprowadzić regresję logistyczną w Pythonie
Jak przeprowadzić regresję wykładniczą w Pythonie
Jak obliczyć AIC modeli regresji w Pythonie