Statystyki opisowe lub wnioskowane: jaka jest różnica?

Istnieją dwie główne gałęzie w dziedzinie statystyki:

• Opisowe statystyki
• Statystyka wnioskowania

W tym samouczku wyjaśniono różnicę między tymi dwiema gałęziami i dlaczego każda z nich jest przydatna w określonych sytuacjach.

Statystyki opisowe

Krótko mówiąc, statystyka opisowa ma na celu opisanie zestawu surowych danych za pomocą statystyk podsumowujących, wykresów i tabel.

Statystyki opisowe są przydatne, ponieważ pozwalają zrozumieć grupę danych znacznie szybciej i łatwiej niż tylko przeglądanie wierszy i wierszy nieprzetworzonych wartości danych.

Załóżmy na przykład, że mamy surowy zbiór danych przedstawiający wyniki testów 1000 uczniów w określonej szkole. Możemy być zainteresowani średnim wynikiem testu, a także rozkładem wyników testu.

Korzystając ze statystyk opisowych, możemy znaleźć średni wynik i stworzyć wykres, który pomoże nam zwizualizować rozkład wyników.

Dzięki temu możemy znacznie łatwiej zrozumieć wyniki testów uczniów, niż tylko przeglądanie surowych danych.

Typowe formy statystyki opisowej

Istnieją trzy popularne formy statystyki opisowej:

1. Statystyki podsumowujące. Są to statystyki podsumowujące dane za pomocą jednej liczby. Istnieją dwa popularne typy statystyk podsumowujących:

• Miary tendencji centralnej : Liczby te opisują, gdzie znajduje się środek zbioru danych. Przykłady obejmują średnią   i mediana .
• Miary dyspersji: Liczby te opisują rozkład wartości w zbiorze danych. Przykłady obejmują przedział , rozstęp międzykwartylowy , odchylenie standardowe i wariancję .

2. Grafika . Wykresy pomagają nam wizualizować dane. Typowe typy wykresów używanych do wizualizacji danych obejmują wykresy pudełkowe , histogramy , wykresy łodyg i liści oraz wykresy punktowe .

3. Tabele . Tabele mogą pomóc nam zrozumieć, w jaki sposób dane są dystrybuowane. Powszechnym typem tabeli jest tabela częstotliwości , która informuje nas, ile wartości danych mieści się w określonych zakresach.

Przykład wykorzystania statystyki opisowej

Poniższy przykład ilustruje, jak możemy wykorzystać statystyki opisowe w świecie rzeczywistym.

Zakłada się, że 1000 uczniów w określonej szkole przystępuje do tego samego testu. Chcemy zrozumieć rozkład wyników testów, dlatego korzystamy z następujących statystyk opisowych:

1. Statystyki podsumowujące

Średnia: 82,13 . To mówi nam, że średni wynik testu wśród 1000 uczniów wynosi 82,13.

Mediana: 84. Oznacza to, że połowa uczniów uzyskała wynik powyżej 84, a druga połowa poniżej 84.

Maks.: 100. Min.: 45. To mówi nam, że maksymalny wynik uzyskany przez dowolnego ucznia wyniósł 100, a minimalny wynik to 45. Rozstęp – który mówi nam różnicę między maksimum a minimum – wynosi 55.

2. Grafika

Aby zwizualizować rozkład wyników testów, możemy utworzyć histogram – rodzaj wykresu, który wykorzystuje prostokątne słupki do przedstawienia częstotliwości.

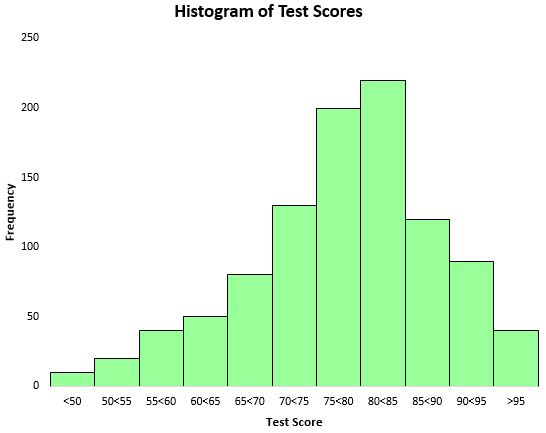
Na podstawie tego histogramu widzimy, że rozkład wyników testów ma z grubsza kształt dzwonu. Większość uczniów uzyskała wynik pomiędzy 70 a 90, bardzo niewielu uzyskało wynik powyżej 95, a jeszcze mniej poniżej 50.

3. Stoły

Innym łatwym sposobem zrozumienia rozkładu wyników jest utworzenie tabeli częstości. Na przykład poniższa tabela częstości pokazuje odsetek uczniów, którzy uzyskali wyniki w różnych zakresach:

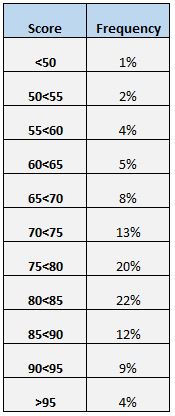
Widzimy, że tylko 4% wszystkich uczniów uzyskało wynik powyżej 95. Widzimy również, że (12% + 9% + 4% = ) 25% wszystkich uczniów uzyskało wynik 85 lub więcej.

Tabela częstości jest szczególnie przydatna, jeśli chcemy wiedzieć, jaki procent wartości danych jest powyżej lub poniżej określonej wartości. Załóżmy na przykład, że szkoła uznaje każdy wynik powyżej 75 za „akceptowalny” wynik testu.

Patrząc na tabelę częstości łatwo zauważyć, że (20% + 22% + 12% + 9% + 4% = ) 67% uczniów uzyskało akceptowalny wynik na teście.

Statystyka wnioskowania

Krótko mówiąc, statystyka wnioskowania wykorzystuje małą próbkę danych w celu wyciągnięcia wniosków na temat większej populacji, z której pobierana jest próba.

Na przykład możemy chcieć zrozumieć preferencje polityczne milionów ludzi w danym kraju.

Jednakże badanie każdej osoby w kraju byłoby zbyt czasochłonne i kosztowne. Zamiast tego przeprowadzilibyśmy mniejszą ankietę, powiedzmy na 1000 Amerykanów, i wykorzystalibyśmy jej wyniki do wyciągnięcia wniosków na temat całej populacji.

Oto całe założenie statystyki wnioskowania: chcemy odpowiedzieć na pytanie dotyczące populacji, więc uzyskujemy dane dla małej próby tej populacji i wykorzystujemy te dane do wyciągania wniosków na temat populacji.

Znaczenie próby reprezentatywnej

Aby mieć pewność, że potrafimy wykorzystać próbę do wyciągnięcia wniosków na temat populacji, musimy upewnić się, że dysponujemy próbą reprezentatywną , to znaczy próbą, w której cechy osobników w populacji są bardzo zbliżone do próby cechy. całej populacji.

Idealnie byłoby, gdyby nasza próba przypominała „mini wersję” naszej populacji. Jeśli zatem chcemy wyciągnąć wnioski na temat populacji uczniów składającej się w 50% z dziewcząt i w 50% z chłopców, nasza próba nie byłaby reprezentatywna, gdyby obejmowała 90% chłopców i tylko 10% dziewcząt.

Jeśli nasza próba nie jest podobna do całej populacji, nie możemy z całą pewnością uogólnić wyników z próby na całą populację.

Jak uzyskać reprezentatywną próbkę

Aby zmaksymalizować szanse na uzyskanie reprezentatywnej próbki, należy skupić się na dwóch rzeczach:

1. Upewnij się, że używasz metody losowego próbkowania.

Istnieje kilka metod losowego pobierania próbek , które pozwolą uzyskać reprezentatywną próbkę, w tym:

• Prosta losowa próbka
• Systematyczna próbka losowa
• Losowa próbka klastra
• Warstwowa próbka losowa

Metody losowego doboru próby dają zazwyczaj próbki reprezentatywne, ponieważ każdy członek populacji ma równe szanse na włączenie do próby.

2. Upewnij się, że wielkość próbki jest wystarczająco duża .

Oprócz zastosowania odpowiedniej metody próbkowania ważne jest, aby upewnić się, że próba jest wystarczająco duża, aby dysponować wystarczającą ilością danych, aby móc uogólniać na większą populację.

Aby określić wielkość próby, należy wziąć pod uwagę wielkość badanej populacji, poziom ufności, jaki chcesz zastosować, oraz margines błędu, który uważasz za akceptowalny.

Na szczęście możesz skorzystać z kalkulatorów online, aby wprowadzić te wartości i sprawdzić, jaka powinna być wielkość próbki.

Typowe formy statystyki wnioskowania

Istnieją trzy popularne formy statystyki wnioskowania:

1. Testowanie hipotez.

Często chcemy odpowiedzieć na pytania dotyczące populacji, takie jak:

• Czy odsetek mieszkańców Ohio popierających Kandydata A przekracza 50%?
• Czy średnia wysokość określonej rośliny wynosi 14 cali?
• Czy istnieje różnica pomiędzy średnim wzrostem uczniów w szkole A i szkole B?

Aby odpowiedzieć na te pytania, możemy przeprowadzićtestowanie hipotez , co pozwala nam wykorzystać dane z próby do wyciągnięcia wniosków na temat populacji.

2. Przedziały ufności .

Czasami chcemy oszacować pewną wartość dla populacji. Na przykład może nas interesować średnia wysokość określonego gatunku rośliny w Australii.

Zamiast chodzić i mierzyć każdą roślinę w kraju, moglibyśmy zebrać małą próbkę roślin i zmierzyć każdą z nich. Następnie możemy wykorzystać średnią wysokość roślin w próbie do oszacowania średniego wzrostu populacji.

Jest jednak mało prawdopodobne, aby nasza próba zapewniła doskonałe oszacowanie populacji. Na szczęście możemy wyjaśnić tę niepewność, tworząc przedział ufności , który zapewnia zakres wartości, w ramach którego mamy pewność, że mieści się prawdziwy parametr populacji.

Na przykład moglibyśmy uzyskać 95% przedział ufności wynoszący [13,2, 14,8], co oznacza, że mamy 95% pewności, że rzeczywista średnia wysokość tego gatunku rośliny wynosi od 13,2 cala do 14,8 cala.

3. Regresja .

Czasami chcemy zrozumieć związek między dwiema zmiennymi w populacji.

Załóżmy na przykład, że chcemy wiedzieć, czy godziny spędzone na nauce w tygodniu są powiązane z wynikami testów . Aby odpowiedzieć na to pytanie, moglibyśmy zastosować technikę znaną jako analiza regresji .

Możemy zatem przyjrzeć się liczbie godzin nauki, a także wynikom testów 100 uczniów i przeprowadzić analizę regresji, aby sprawdzić, czy istnieje istotny związek między tymi dwiema zmiennymi.

Jeśli okaże się, że wartość p regresji jest istotna , możemy stwierdzić, że istnieje istotny związek między tymi dwiema zmiennymi w całej populacji uczniów.

Różnica między statystyką opisową a statystyką wnioskowania

Podsumowując, różnicę między statystyką opisową a statystyką wnioskowania można opisać w następujący sposób:

Statystyka opisowa wykorzystuje statystyki podsumowujące, wykresy i tabele do opisu zestawu danych.

Jest to przydatne, ponieważ pomaga nam szybko i łatwo zrozumieć zestaw danych bez konieczności przeglądania wszystkich poszczególnych wartości danych.

Statystyka wnioskowania wykorzystuje próbki do wyciągania wniosków na temat większych populacji.

W zależności od pytania dotyczącego populacji, na które chcesz odpowiedzieć, możesz zdecydować się na zastosowanie jednej lub więcej z następujących metod: testowanie hipotez, przedziały ufności i analiza regresji.

Jeśli zdecydujesz się na zastosowanie jednej z tych metod, pamiętaj, że Twoja próba musi być reprezentatywna dla Twojej populacji , w przeciwnym razie wyciągnięte przez Ciebie wnioski nie będą wiarygodne.