Ludność oznacza

Przez Benjamin Anderson 3 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniono, co oznacza populacja w statystyce. Podobnie dowiesz się, jaki jest wzór na średnią populacji, jak obliczany jest przedział ufności średniej populacji, a ponadto jaka jest różnica między średnią populacji a średnią „próbki”.

Jaka jest średnia populacji?

Średnia populacji jest średnią arytmetyczną wszystkich elementów populacji statystycznej. Dlatego, aby obliczyć średnią populacji, należy dodać wszystkie wartości populacji, a następnie podzielić przez całkowitą liczbę elementów w populacji.

Symbolem średniej populacji jest grecka litera μ.

Podobnie średnią populacji można również zdefiniować jako oczekiwaną wartość zmiennej reprezentującej populację.

Jak obliczyć średnią populacji

Kiedy już zapoznaliśmy się z definicją średniej populacji, przyjrzyjmy się, jak obliczana jest średnia populacyjna, aby lepiej zrozumieć jej znaczenie.

Jeżeli znane są wszystkie wartości w populacji statystycznej, do obliczenia średniej populacji należy po prostu zastosować wzór na średnią arytmetyczną. Zatem w tym przypadku, aby obliczyć średnią populacji, musimy dodać wszystkie wartości populacji, a następnie podzielić przez całkowitą liczbę danych.

Jeśli zatem znamy wartość wszystkich elementów populacji, wzór na obliczenie średniej populacji jest następujący:

$\displaystyle\mu=\frac{\displaystyle \sum_{i=1}^N x_i}{N}=\frac{x_1+x_2+\dots +x_N}{N}$

➤ Zobacz: Przykład obliczenia średniej arytmetycznej

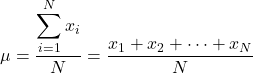
Jednak ogólnie rzecz biorąc, nie wszystkie wartości populacji są znane, dlatego zwykle wartość średniej populacji jest szacowana za pomocą przedziałów .

Przedział ufności dla średniej populacji

W praktyce nie ma możliwości zbadania wszystkich osobników w populacji, dlatego zazwyczaj wybiera się losową próbę z populacji i na podstawie jej wartości dokonuje się przybliżenia wartości średniej populacji. Dokładniej, obliczamy przedział, w którym z dużym prawdopodobieństwem będzie znajdować się średnia dla całej populacji; przedział ten nazywany jest przedziałem ufności dla średniej populacji.

Przedział ufności dla średniej populacji oblicza się, dodając i odejmując od średniej próbki wartość Z _α/2 pomnożoną przez odchylenie standardowe (σ) i podzieloną przez pierwiastek kwadratowy wzrostu próbki (n). Zatem wzór na obliczenie przedziału ufności dla średniej populacji jest następujący:

$\displaystyle \left(\overline{x}-z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \ , \ \overline{x}+z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \right)$

Powyższy wzór stosuje się, gdy znana jest wariancja populacji. Jeśli jednak wariancja populacji jest nieznana, co jest najczęstszym przypadkiem, przedział ufności dla średniej oblicza się za pomocą następującego wzoru:

$\displaystyle \left(\overline{x}-t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \ , \ \overline{x}+t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \right)$

Złoto:

$\overline{x}$

to przykładowe środki.
$t_{\alpha/2}$

jest wartością rozkładu t-Studenta n-1 stopni swobody z prawdopodobieństwem α/2. Dla dużych próbek i poziomu ufności 95% jest to zwykle bliskie 1,96, a dla poziomu ufności 99% jest zwykle bliskie 2,576.
$s$

jest odchyleniem standardowym próbki.
$n$

to wielkość próbki.

➤ Zobacz: Przykład obliczenia przedziału ufności dla średniej populacji

Średnia populacji i średnia próbki

Na koniec, podsumowując, dokonamy przeglądu różnic między średnią populacji a średnią próbki, aby te dwie koncepcje statystyczne były jasne.

Różnica między średnią populacji a średnią próbki to zakres wartości, dla których obliczana jest średnia. Średnia populacji to średnia całej populacji statystycznej, natomiast średnia próby to średnia próbki populacji.

Dodatkowo, aby odróżnić średnią populacji od średniej próbki, są one oznaczone różnymi symbolami. Symbol oznaczający populację to

$\mu$

, z drugiej strony, symbolem środków próbki jest

$\overline{x}$

$\begin{array}{c}\mu =\text{Media poblacional}\\[2ex]\overline{x} = \text{Media muestral}\end{array}$

Jeśli nadal masz wątpliwości co do różnic pomiędzy tymi dwoma typami średnich lub chcesz dowiedzieć się więcej na temat obliczania średniej z próby, możesz zapoznać się z poniższym artykułem:

➤ Zobacz: Co oznacza próbka?

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej