Percentyl, kwartyl i kwantyl: jaka jest różnica?

Trzy terminy, które uczniowie często mylą w statystyce, to percentyle, kwartyle i kwantyle.

Oto prosta definicja każdego z nich:

Percentyle: zakres od 0 do 100.

Kwartyle: zakres od 0 do 4.

Kwantyle: przejdź od dowolnej wartości do dowolnej innej wartości.

Należy pamiętać, że percentyle i kwartyle to po prostu rodzaje kwantyli.

Niektóre typy kwantyli mają nawet specyficzne nazwy, na przykład:

• Cztery kwantyle nazywane są kwartylami .
• Pięć kwantyli nazywa się kwintylami .
• 8 kwantyli nazywa się oktylami .
• 10 kwantyli nazywa się decylami .
• 100 kwantyli nazywa się percentylami .

Należy zauważyć, że percentyle i kwartyle łączy następująca zależność:

• 0 percentyl = 0 kwartyl (zwany także minimum)
• 25. percentyl = 1. kwartyl
• 50. percentyl = 2. kwartyl (zwany także medianą)
• 75. percentyl = 3. kwartyl
• 100. percentyl = 4. kwartyl (zwany także maksimum)

Przykład: Znajdowanie percentyli i kwartylów

Załóżmy, że mamy następujący zbiór danych zawierający 20 wartości:

Korzystając z oprogramowania statystycznego (takiego jak Excel, R, Python itp.), możemy znaleźć następujące percentyle i kwartyle dla tego zbioru danych:

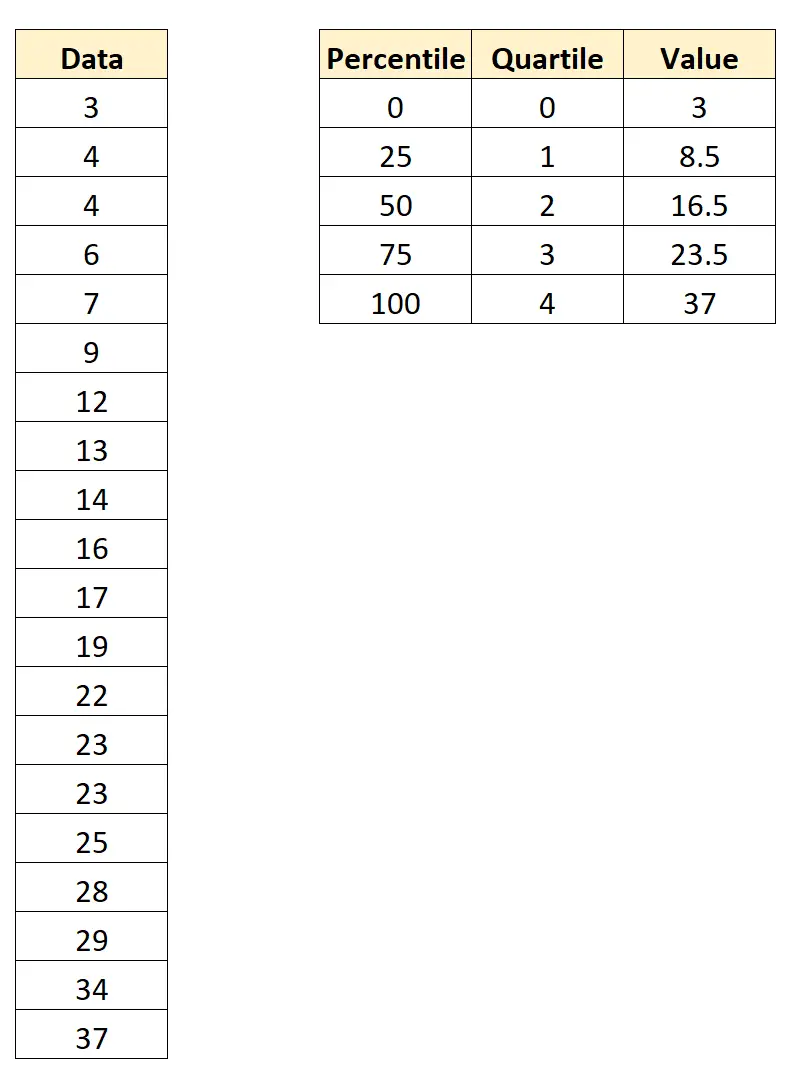
Oto jak interpretować te wartości:

• Percentyl 0 i kwartyl 0 to 3 .
• 25. percentyl i 1. kwartyl to 8,5 .
• 50. percentyl i 2. kwartyl to 16,5 .
• 75. percentyl i 3. kwartyl to 23,5 .
• Setny percentyl i czwarty kwartyl to 37 .

Kiedy stosować percentyle a kiedy kwartyle

Percentyle można wykorzystać do odpowiedzi na pytania takie jak:

Ile uczeń musi zdobyć w konkretnym teście, aby znaleźć się w najlepszych 10%?

Aby odpowiedzieć na to pytanie, znaleźlibyśmy 90. percentyl wszystkich wyników, czyli wartość oddzielającą 90% dolnych od 10% górnych.

Jaki wzrost obejmuje 40% średniego wzrostu uczniów w danej szkole?

Aby odpowiedzieć na to pytanie, znaleźlibyśmy 70. percentyl wzrostu i 30. percentyl wzrostu, czyli dwie wartości określające górną i dolną granicę środkowych 40% wzrostu.

Kwartyli można używać do odpowiadania na pytania takie jak:

Ile uczeń musi zdobyć na teście, aby znaleźć się w górnej ćwiartce wyników?

Aby odpowiedzieć na to pytanie, znaleźlibyśmy trzeci kwartyl wszystkich wyników, czyli wartość oddzielającą 75% dolnych od 25% górnych.

Jaki jest rozstęp międzykwartylowy danego zbioru danych?

Rozstęp międzykwartylowy (IQR) to zakres środkowych 50% wartości danych. Aby znaleźć IQR dla danego zbioru danych, możemy obliczyć 3. kwartyl – 1. kwartyl.

Dodatkowe zasoby

Jak obliczyć percentyle w R
Jak obliczyć kwartyle w R
Jak obliczyć rozstęp międzykwartylowy w programie Excel
Jak obliczyć rozstęp międzykwartylowy na kalkulatorze TI-84