Jak obliczyć średni błąd kwadratowy (rmse) w programie excel

W statystyce analiza regresji jest techniką, której używamy do zrozumienia związku między zmienną predykcyjną x i zmienną odpowiedzi y.

Kiedy przeprowadzamy analizę regresji, otrzymujemy model, który informuje nas o przewidywanej wartości zmiennej odpowiedzi na podstawie wartości zmiennej predykcyjnej.

Jednym ze sposobów oceny, jak dobrze nasz model pasuje do danego zbioru danych, jest obliczenie błędu średniokwadratowego , który jest metryką, która mówi nam, jak średnio nasze przewidywane wartości różnią się od wartości obserwowanych.

Wzór na znalezienie błędu średniokwadratowego, bardziej znany jako RMSE , jest następujący:

RMSE = √[ Σ(P _ja – O _ja ) ² / n ]

Złoto:

• Σ to fantazyjny symbol oznaczający „sumę”
• _Pi jest przewidywaną wartością ^i-tej obserwacji w zbiorze danych
• O _i jest obserwowaną wartością ^i-tej obserwacji w zbiorze danych
• n to wielkość próbki

Uwagi techniczne :

• Błąd średniokwadratowy można obliczyć dla dowolnego typu modelu, który generuje przewidywane wartości, które następnie można porównać z obserwowanymi wartościami zbioru danych.
• Błąd średniokwadratowy jest czasami nazywany odchyleniem średniokwadratowym i często jest określany w skrócie RMSD.

Następnie spójrzmy na przykład obliczania błędu średniokwadratowego w programie Excel.

Jak obliczyć średni błąd kwadratowy w programie Excel

W programie Excel nie ma wbudowanej funkcji obliczania RMSE, ale możemy to obliczyć dość łatwo za pomocą jednej formuły. Pokażemy, jak obliczyć RMSE dla dwóch różnych scenariuszy.

Scenariusz 1

W scenariuszu możesz mieć jedną kolumnę zawierającą przewidywane wartości z Twojego modelu i drugą kolumnę zawierającą wartości zaobserwowane. Poniższy obrazek przedstawia przykład takiego scenariusza:

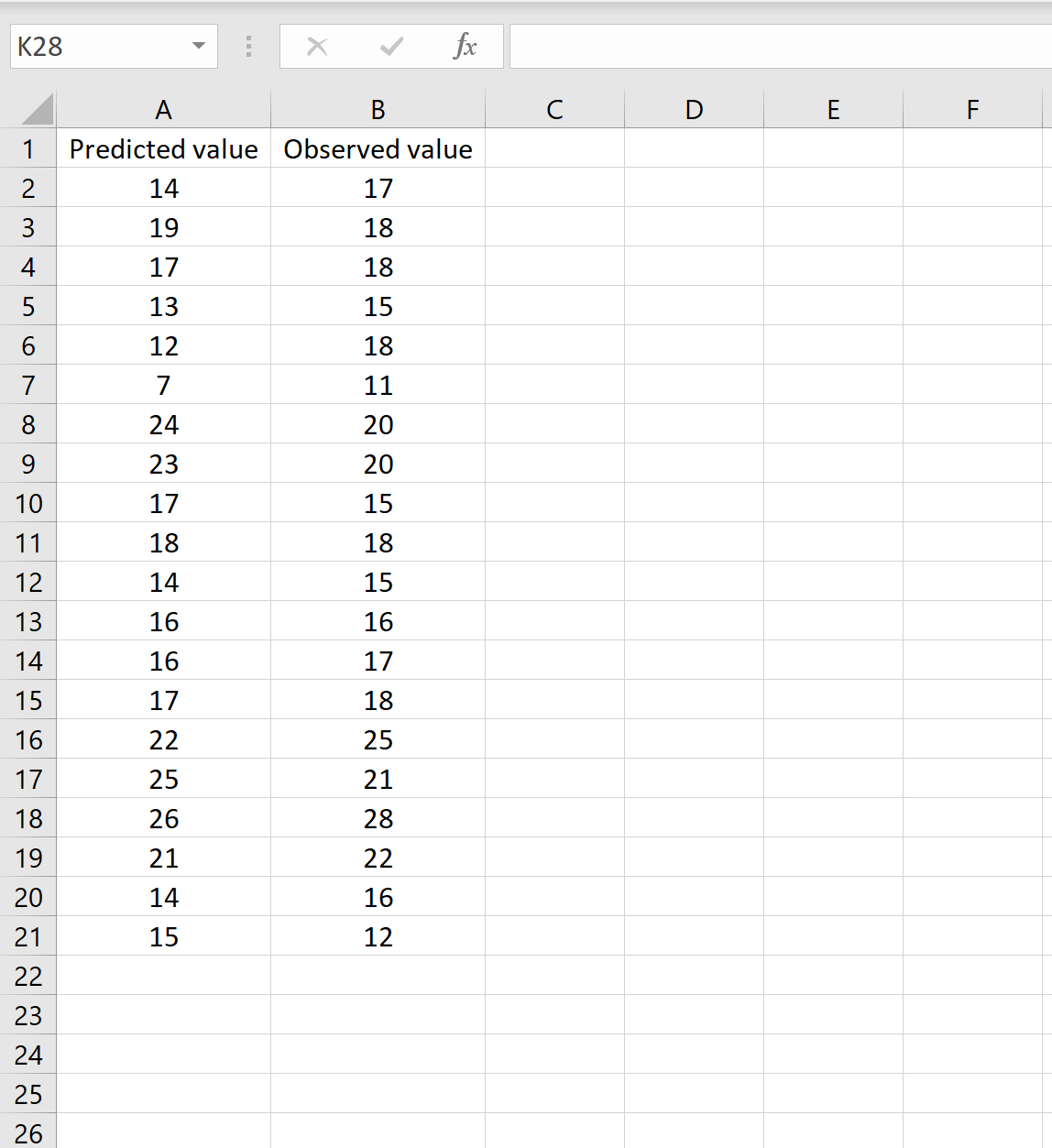
Jeśli tak, możesz obliczyć RMSE, wpisując następującą formułę w dowolnej komórce, a następnie klikając CTRL+SHIFT+ENTER:

=KWADRAT(SUMSQ(A2:A21-B2:B21) / LICZBA(A2:A21))

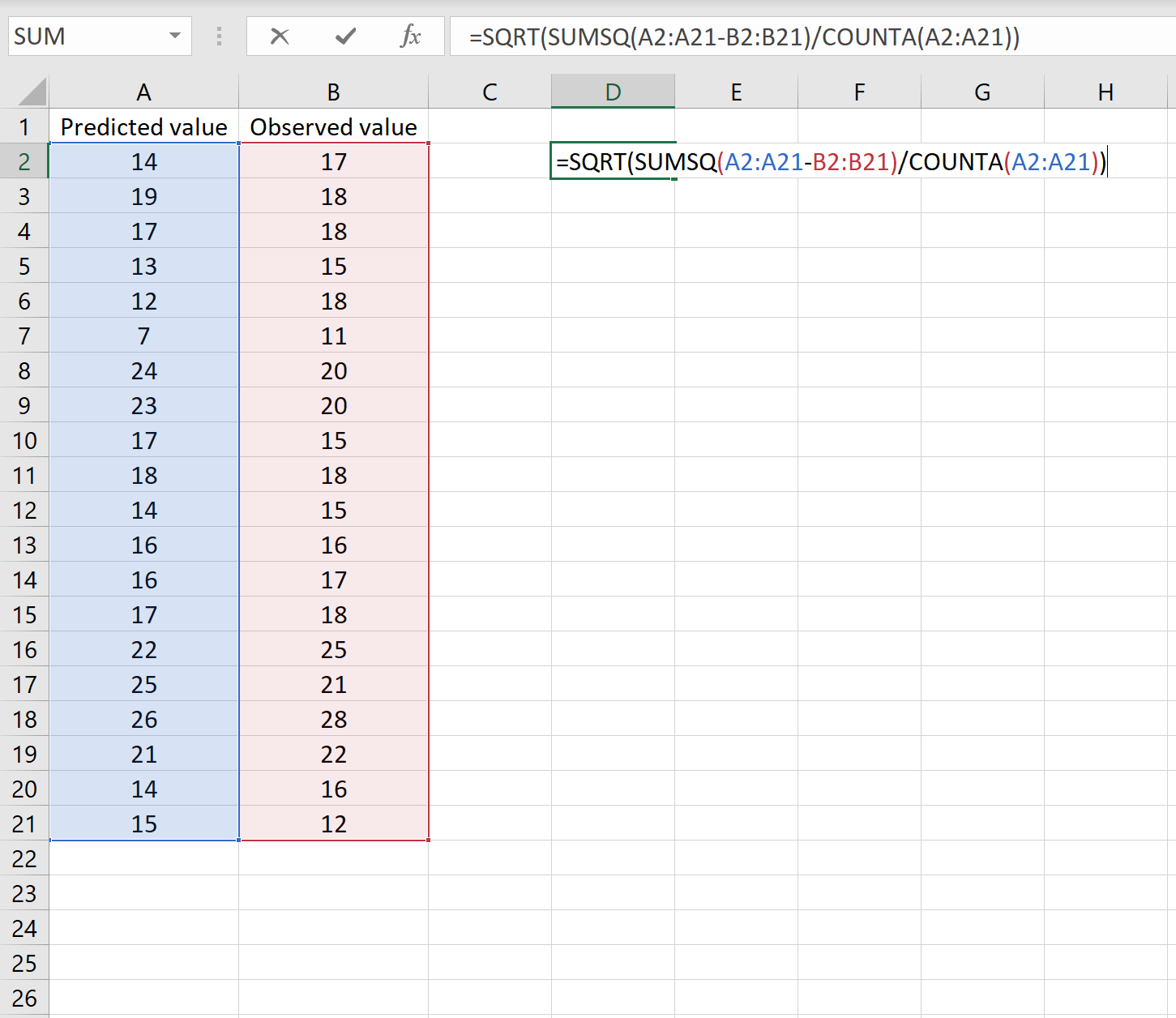
To mówi nam, że średni błąd kwadratowy wynosi 2,6646 .

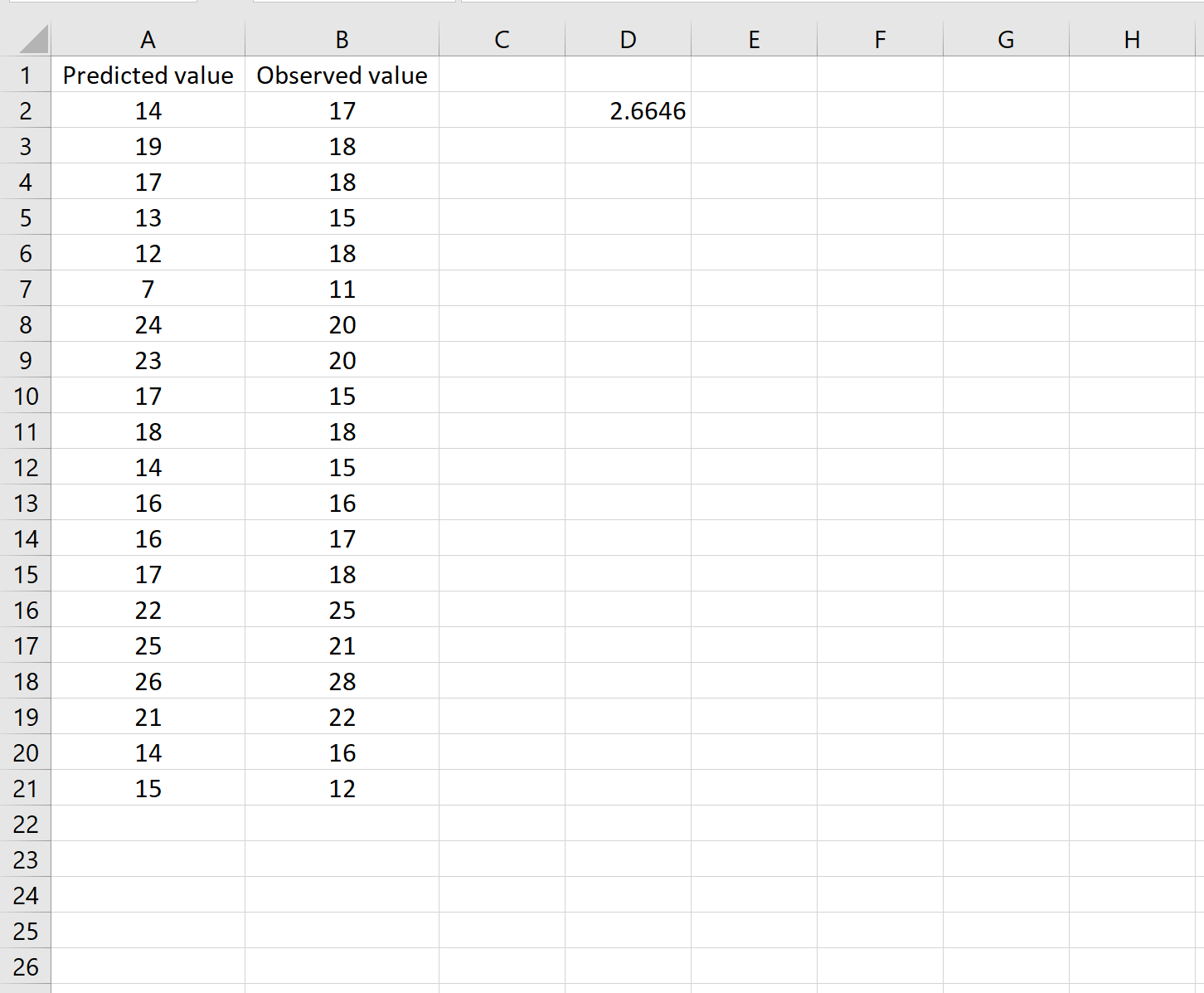
Formuła może wydawać się nieco skomplikowana, ale ma sens, gdy ją rozłożysz:

= KWADRAT( SUMSQ(A2:A21-B2:B21) / LICZBA(A2:A21) )

• Najpierw obliczamy sumę kwadratów różnic między wartościami przewidywanymi i obserwowanymi za pomocą funkcji SUMSQ() .
• Następnie dzielimy przez wielkość próbki zbioru danych za pomocą funkcji COUNTA() , która zlicza liczbę komórek w zakresie, które nie są puste.
• Na koniec wyciągamy pierwiastek kwadratowy z całego obliczenia za pomocą funkcji SQRT() .

Scenariusz 2

W innym scenariuszu być może już obliczyłeś różnice między wartościami przewidywanymi i obserwowanymi. W tym przypadku będziesz mieć tylko jedną kolumnę pokazującą różnice.

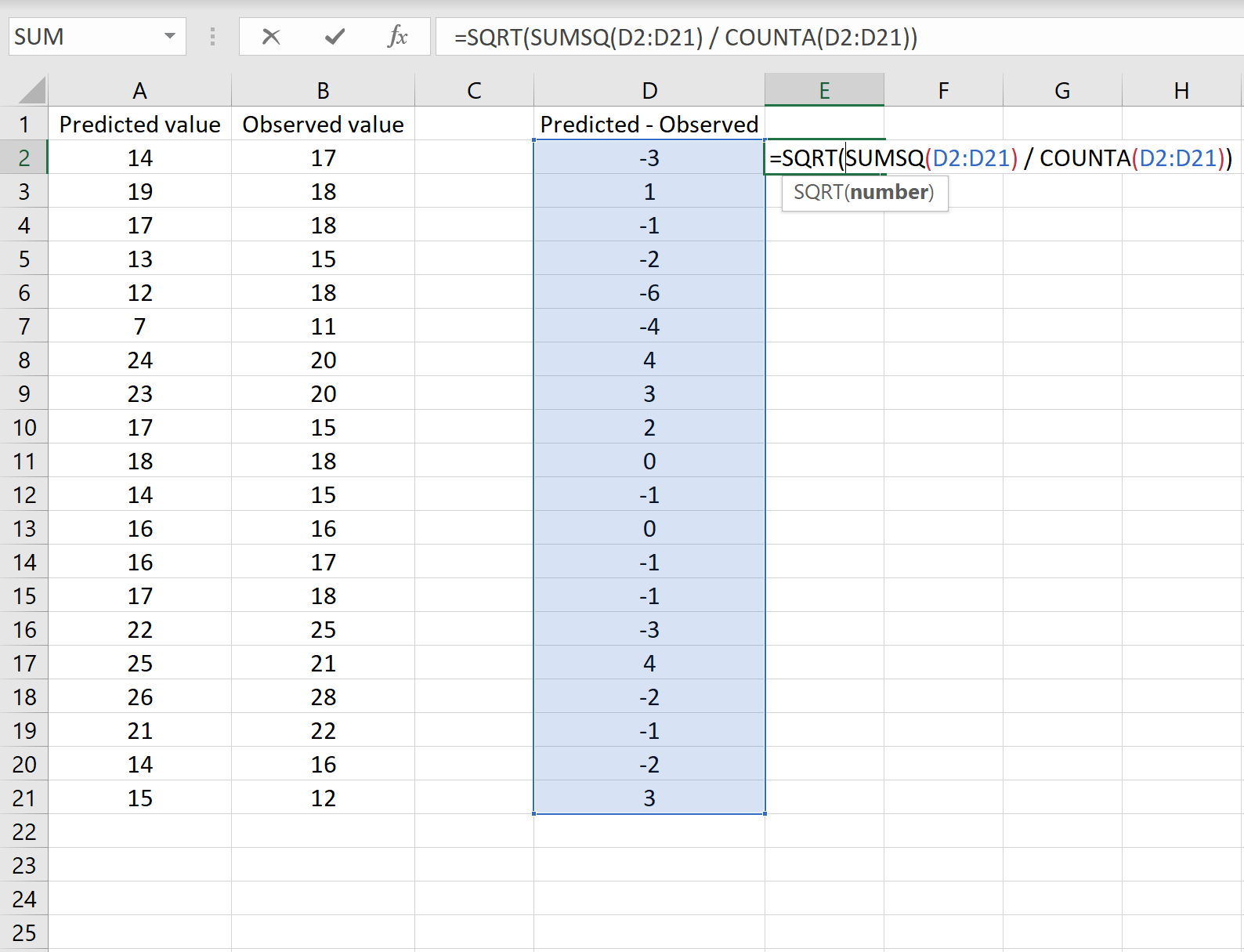
Poniższy obrazek przedstawia przykład takiego scenariusza. Przewidywane wartości pokazano w kolumnie A, zaobserwowane wartości w kolumnie B, a różnicę między przewidywanymi i zaobserwowanymi wartościami w kolumnie D:

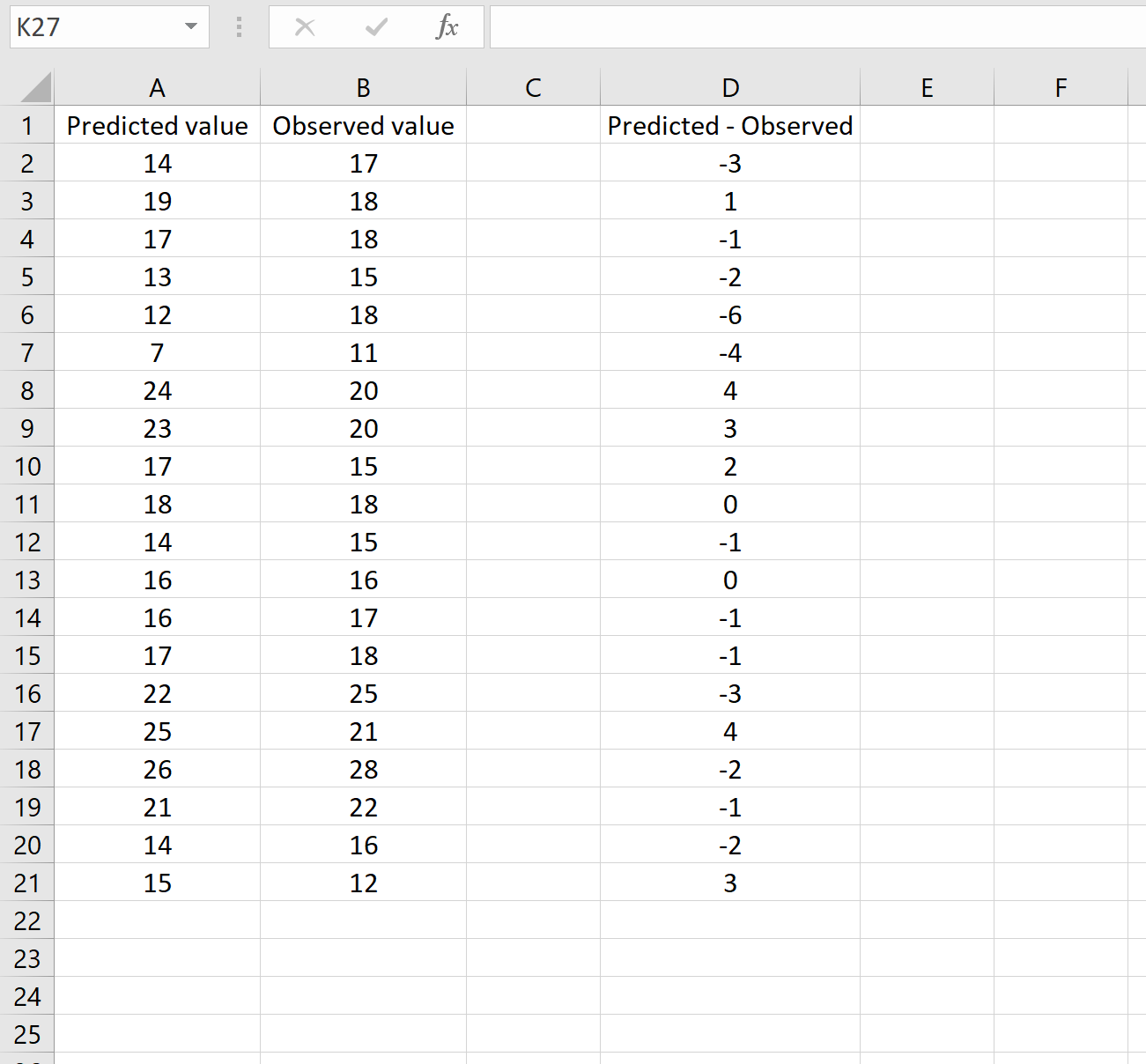
Jeśli tak, możesz obliczyć RMSE, wpisując następującą formułę w dowolnej komórce, a następnie klikając CTRL+SHIFT+ENTER:

=KWADRAT(SUMSQ(D2:D21) / LICZBA(D2:D21))

Mówi nam to, że błąd średniokwadratowy wynosi 2,6646 , co odpowiada wynikowi uzyskanemu w pierwszym scenariuszu. Potwierdza to, że te dwa podejścia do obliczania RMSE są równoważne.

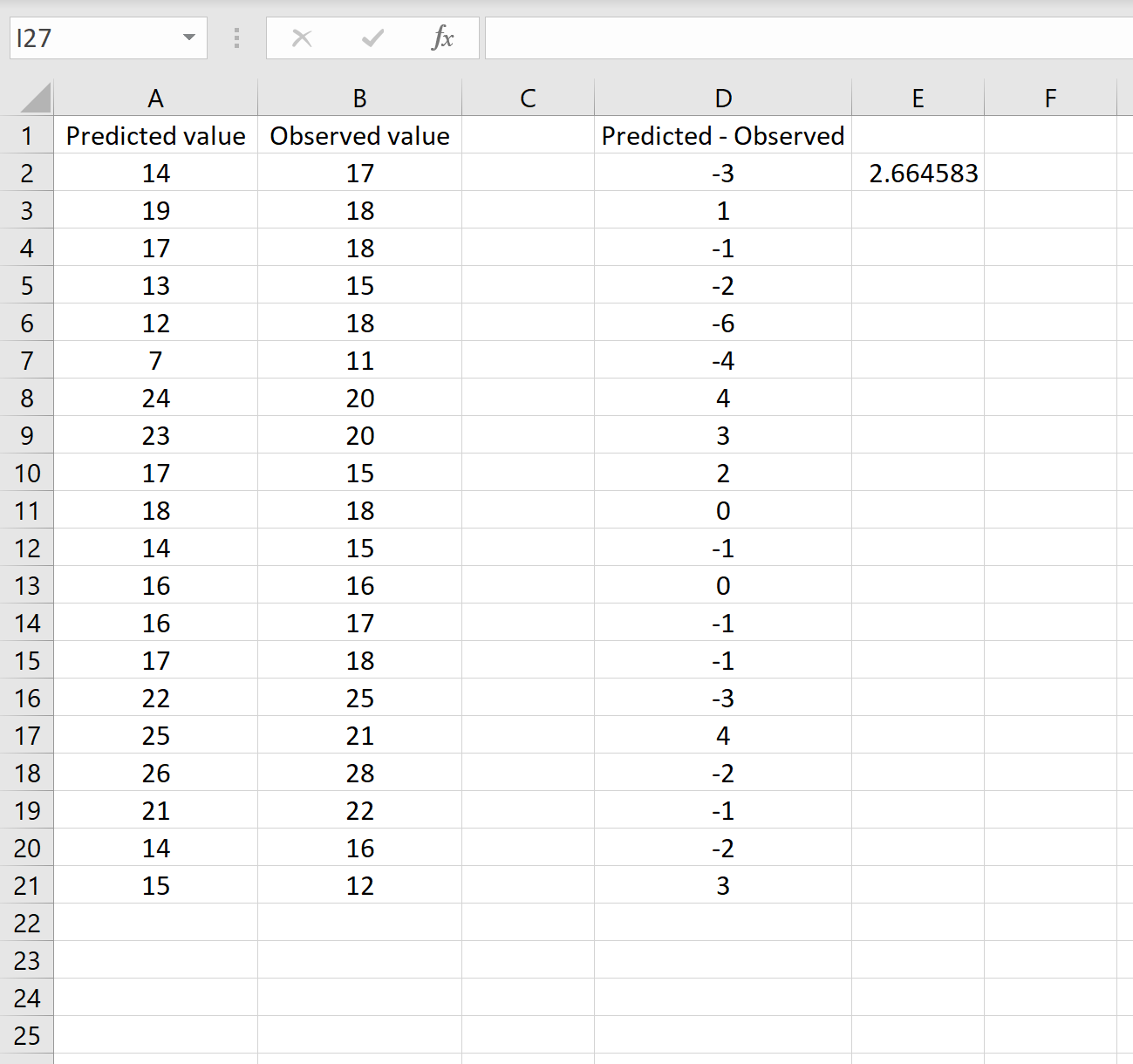
Formuła, której użyliśmy w tym scenariuszu, tylko nieznacznie różni się od tej, którą zastosowaliśmy w poprzednim scenariuszu:

= KWRT( SUMSQ(D2:D21) / LICZBA(D2:D21) )

• Ponieważ w kolumnie D obliczyliśmy już różnice pomiędzy wartościami przewidywanymi i zaobserwowanymi, możemy obliczyć sumę kwadratów różnic za pomocą funkcji SUMSQ().   funkcję tylko z wartościami z kolumny D.
• Następnie dzielimy przez wielkość próbki zbioru danych za pomocą funkcji COUNTA() , która zlicza liczbę komórek w zakresie, które nie są puste.
• Na koniec wyciągamy pierwiastek kwadratowy z całego obliczenia za pomocą funkcji SQRT() .

Jak interpretować RMSE

Jak wspomniano wcześniej, RMSE to przydatny sposób sprawdzenia, jak dobrze model regresji (lub dowolny model generujący przewidywane wartości) jest w stanie „dopasować” zbiór danych.

Im większy RMSE, tym większa różnica między wartościami przewidywanymi i obserwowanymi, co oznacza, że model regresji gorzej pasuje do danych. I odwrotnie, im mniejszy RMSE, tym lepiej model jest w stanie dopasować dane.

Szczególnie przydatne może być porównanie RMSE dwóch różnych modeli, aby sprawdzić, który model najlepiej pasuje do danych.

Aby uzyskać więcej samouczków dotyczących programu Excel, odwiedź naszą stronę Przewodniki po programie Excel , na której znajdują się wszystkie samouczki dotyczące programu Excel dotyczące statystyk.