Pominięte zmienne obciążenie: definicja i przykłady

Pominięte obciążenie zmiennej ma miejsce, gdy odpowiednia zmienna objaśniająca nie jest uwzględniona w modelu regresji , co może skutkować odchyleniem współczynnika jednej lub większej liczby zmiennych objaśniających w modelu.

Pominięta zmienna jest często wykluczana z modelu regresji z jednego z dwóch powodów:

1. Dane dla zmiennej są po prostu niedostępne.

2. Wpływ zmiennej objaśniającej na zmienną odpowiedzi jest nieznany.

Aby pominięta zmienna faktycznie zniekształcała współczynniki modelu, muszą zostać spełnione dwa warunki:

1. Pominięta zmienna musi być skorelowana z jedną lub większą liczbą zmiennych objaśniających w modelu.

2. Pominiętą zmienną należy skorelować ze zmienną odpowiedzi w modelu.

Skutki pominiętego odchylenia zmiennej

Załóżmy, że mamy dwie zmienne objaśniające, A i B, oraz zmienną odpowiedzi Y. Załóżmy, że dopasowujemy prosty model regresji liniowej z A jako jedyną zmienną objaśniającą i pomijamy B w modelu.

Jeśli B jest skorelowane z A i skorelowane z Y, spowoduje to błąd w oszacowaniu współczynnika A. Poniższy diagram pokazuje, w jaki sposób oszacowanie współczynnika A będzie obciążone, w zależności od charakteru związku z B:

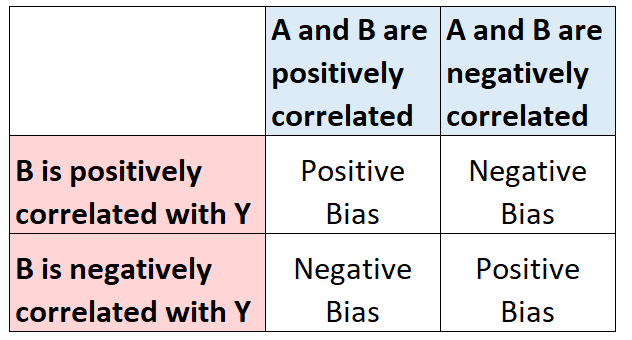
Przykład: pominięte zmienne obciążenie

Załóżmy, że chcemy zbadać wpływ metrażu na cenę nieruchomości i dlatego stosujemy następujący prosty model regresji liniowej:

Cena domu = B ₀ + B ₁ (powierzchnia kwadratowa)

Załóżmy, że oszacowany model to:

Cena domu = 40 203,91 + 118,31 (pow. kwadratowa)

Sposób, w jaki interpretujemy współczynnik metra kwadratowego, jest taki, że każdy dodatkowy wzrost o jedną jednostkę metra kwadratowego wiąże się ze wzrostem ceny domu średnio o 118,31 USD.

Załóżmy jednak, że pominiemy zmienną objaśniającą wiek , która okazuje się silnie ujemnie skorelowana z metrażem kwadratowym i silnie ujemnie skorelowana z ceną nieruchomości. Ta zmienna powinna znajdować się w modelu, ale jej nie ma. Zatem oszacowanie współczynnika dla metra kwadratowego jest prawdopodobnie stronnicze.

Ponieważ wiek jest ujemnie skorelowany zarówno ze zmienną objaśniającą, jak i odpowiedzią w modelu, spodziewamy się, że oszacowanie współczynnika dla powierzchni kwadratowej będzie dodatnio obciążone:

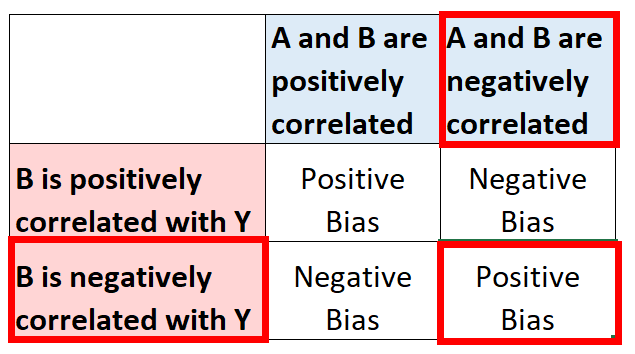
Załóżmy, że znajdziemy dane dotyczące wieku mieszkania i następnie uwzględnimy je w modelu. Model staje się wówczas:

Cena domu = B ₀ + B ₁ (powierzchnia kwadratowa) + B ₂ (wiek)

Załóżmy, że oszacowany model to:

Cena domu = 123 426,20 + 81,06 (pow. kwadratowa) – 1 291,04 (wiek)

Należy zauważyć, że oszacowanie współczynnika dla metra kwadratowego znacznie się zmniejszyło, co oznacza, że w poprzednim modelu było dodatnio obciążone.

Sposób, w jaki interpretujemy współczynnik metra kwadratowego w tym modelu, jest taki, że każdy dodatkowy wzrost o jedną jednostkę metra kwadratowego wiąże się ze średnim wzrostem ceny domu o 81,06 USD, przy założeniu, że wiek pozostaje stały.

Co zrobić z pominiętym odchyleniem zmiennych

Niestety, w świecie rzeczywistym często zdarza się, że obciążenie pominiętymi zmiennymi często występuje, ponieważ pewne zmienne powinny generalnie zostać uwzględnione w modelu regresji, ale tak się nie dzieje, ponieważ dane na ich temat nie są dostępne lub związek między nimi a zmienną odpowiedzi jest nieznany.

Jeśli to możliwe, powinieneś spróbować uwzględnić wszystkie istotne zmienne objaśniające w modelu regresji, aby zrozumieć prawdziwy związek między zmiennymi objaśniającymi a zmienną odpowiedzi.

Wyłączenie odpowiednich zmiennych objaśniających z modelu może znacząco wpłynąć na interpretację modelu, jak widzieliśmy w poprzednim przykładzie z cenami nieruchomości.

Dodatkowe zasoby

Co to jest ukryta zmienna?
Co to jest myląca zmienna?