Jak porównać histogramy (z przykładami)

Histogram to rodzaj wykresu, który pozwala nam zwizualizować rozkład wartości w zbiorze danych.

Oś X pokazuje wartości zbioru danych, a oś Y pokazuje częstotliwość każdej wartości.

Histogramy są przydatne, ponieważ pozwalają nam szybko zrozumieć rozkład wartości w zbiorze danych. Są również przydatne do porównywania dwóch różnych zestawów danych.

Porównując dwa lub więcej histogramów, możemy odpowiedzieć na trzy różne pytania:

1. Jak porównują się wartości mediany?

Możemy z grubsza oszacować, że mediana leży w pobliżu środka każdego histogramu, co pozwala nam porównać wartości mediany rozkładów.

2. Jak wypada porównanie dyspersji?

Możemy wizualnie zobaczyć, który histogram jest bardziej rozłożony, co daje nam wyobrażenie, który rozkład ma bardziej rozproszone wartości.

3. Jak wypada asymetria?

Jeśli histogram ma „ogon” po lewej stronie wykresu, mówi się, że jest on przekrzywiony ujemnie. I odwrotnie, jeśli histogram ma „ogon” po prawej stronie wykresu, mówi się, że jest on dodatnio przekrzywiony. Możemy wizualnie sprawdzić każdy histogram, aby porównać skośność .

Poniższy przykład pokazuje, jak porównać dwa różne histogramy i odpowiedzieć na te trzy pytania.

Przykład: porównywanie histogramów

Założono, że 200 uczniów korzysta z jednej metody nauki, aby przygotować się do egzaminu, a kolejnych 200 uczniów korzysta z innej metody nauki, aby przygotować się do tego samego egzaminu.

Załóżmy, że tworzymy następujące histogramy w celu porównania wyników egzaminów każdej grupy uczniów:

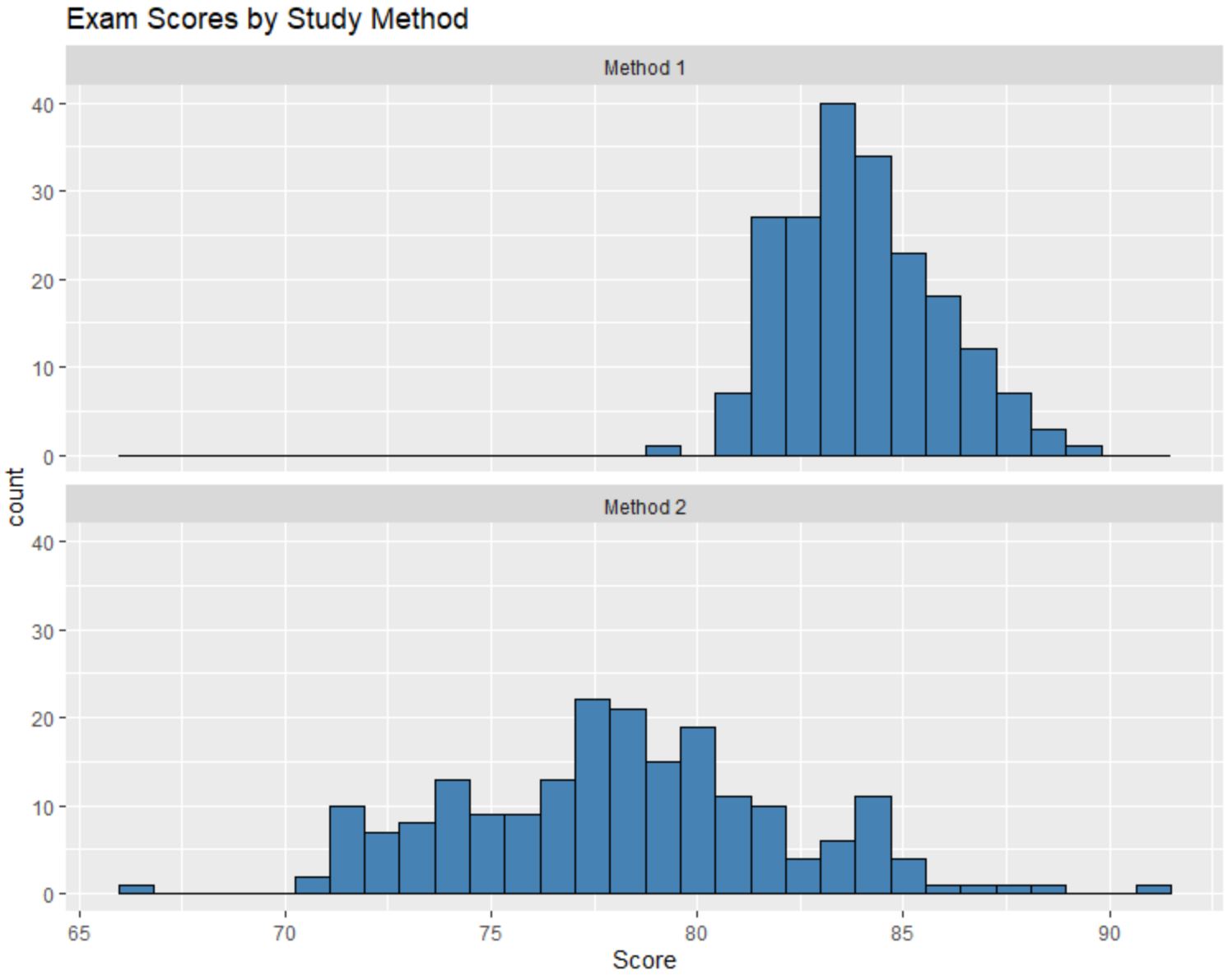
Możemy porównać te histogramy i odpowiedzieć na trzy pytania:

1. Jak porównują się wartości mediany?

Chociaż nie znamy dokładnych wartości mediany każdego rozkładu, po prostu patrząc na histogramy, oczywiste jest, że średni wynik egzaminu uczniów, którzy zastosowali Metodę 1, jest wyższy niż średni wynik egzaminu uczniów, którzy zastosowali Metodę 1. metoda 2.

Można oszacować, że mediana wartości dla metody 1 wynosi około 84, a mediana wartości dla metody 2 wynosi około 78.

2. Jak wypada porównanie dyspersji?

Wartości histogramu dla Metody 2 są znacznie bardziej rozproszone niż te dla Metody 1, co mówi nam, że istnieje znacznie większe rozproszenie wyników egzaminów dla uczniów, którzy zastosowali Metodę 2.

3. Jak wypada asymetria?

Patrząc na histogramy, wydaje się, że rozkład wyników testu dla Metody 1 jest lekko przesunięty w prawo, na co wskazuje „ogon” rozciągający się na prawo od histogramu.

Jednakże nie wydaje się, aby w rozkładzie wyników badania dla metody 2 istniał „ogon”, co oznacza, że rozkład jest niewielki lub nie jest przekrzywiony.

Bonus : Oto kod, którego użyliśmy w R, aby utworzyć te dwa histogramy:

 library (ggplot2)

#make this example reproducible
set. seeds (0)

#create data frame
df <- data. frame (method=rep(c(' Method 1 ', ' Method 2 '), each= 200 ),
                 Score=c(rnorm( 200 , mean= 84 , sd= 2 ),
                         rnorm( 200 , mean= 78 , sd= 4 )))

#create histogram of scores for each method
ggplot(df, aes(x=Score)) +
  geom_histogram(fill=' steelblue ', color=' black ') +
  facet_wrap(.~method, nrow= 2 ) +
  labs(title=' Exam Scores by Study Method ')

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania z histogramami:

Jak oszacować średnią i medianę dowolnego histogramu
Jak oszacować odchylenie standardowe dowolnego histogramu
Jak opisać kształt histogramów