Jak porównać wykresy pudełkowe: z przykładami

Wykres pudełkowy to rodzaj wykresu przedstawiający pięciocyfrowe podsumowanie zbioru danych, które obejmuje:

• Wartość minimalna
• Pierwszy kwartyl (25. percentyl)
• Wartość średnia
• Trzeci kwartyl (75. percentyl)
• Maksymalna wartość

Aby sporządzić wykres pudełkowy, rysujemy pudełko od pierwszego do trzeciego kwartyla. Następnie rysujemy pionową linię na środku. Na koniec rysujemy „wąsy” kwartylów aż do wartości minimalnej i maksymalnej.

Wykresy pudełkowe są przydatne, ponieważ pozwalają nam szybko zrozumieć rozkład wartości w zbiorze danych. Są również przydatne do porównywania dwóch różnych zestawów danych.

Porównując dwa lub więcej wykresów skrzynkowych, możemy odpowiedzieć na cztery różne pytania:

1. Jak porównują się wartości mediany? Możemy porównać pionową linię w każdym polu, aby określić, który zestaw danych ma wyższą wartość mediany.

2. Jak wypada porównanie dyspersji? Możemy porównać długość każdego pudełka (która reprezentuje odległość między Q1 i Q3 – rozstęp międzykwartylowy), aby określić, który zbiór danych jest większy.

3. Jak wypada asymetria? Im bliżej pierwszego kwartału znajduje się pionowa linia, tym bardziej dodatnio wypaczony jest zbiór danych. Im bliżej trzeciego kwartału znajduje się pionowa linia, tym bardziej przekrzywiony jest zbiór danych.

4. Czy występują wartości odstające? Na wykresach pudełkowych wartości odstające są zwykle reprezentowane przez małe okręgi wystające poza każdy wąs. Obserwację definiuje się jako odstającą, jeżeli spełnia jedno z poniższych kryteriów:

• Jedna obserwacja jest mniejsza niż Q1 – 1,5*IQR
• Obserwacja jest większa niż Q3 + 1,5*IQR

Poniższy przykład pokazuje, jak porównać dwa różne wykresy skrzynkowe i odpowiedzieć na te cztery pytania.

Przykład: porównywanie wykresów pudełkowych

Poniższe zbiory danych przedstawiają wyniki uczniów, którzy zastosowali jedną z dwóch technik nauki w celu przygotowania się do egzaminu:

Metoda 1: 78, 78, 79, 80, 80, 82, 82, 83, 83, 86, 86, 86, 86, 87, 87, 87, 88, 88, 88, 91

Metoda 2: 66, 66, 66, 67, 68, 70, 72, 75, 75, 78, 82, 83, 86, 88, 89, 90, 93, 94, 95, 98

Jeśli utworzymy wykresy skrzynkowe dla każdego zestawu danych, będą one wyglądać tak:

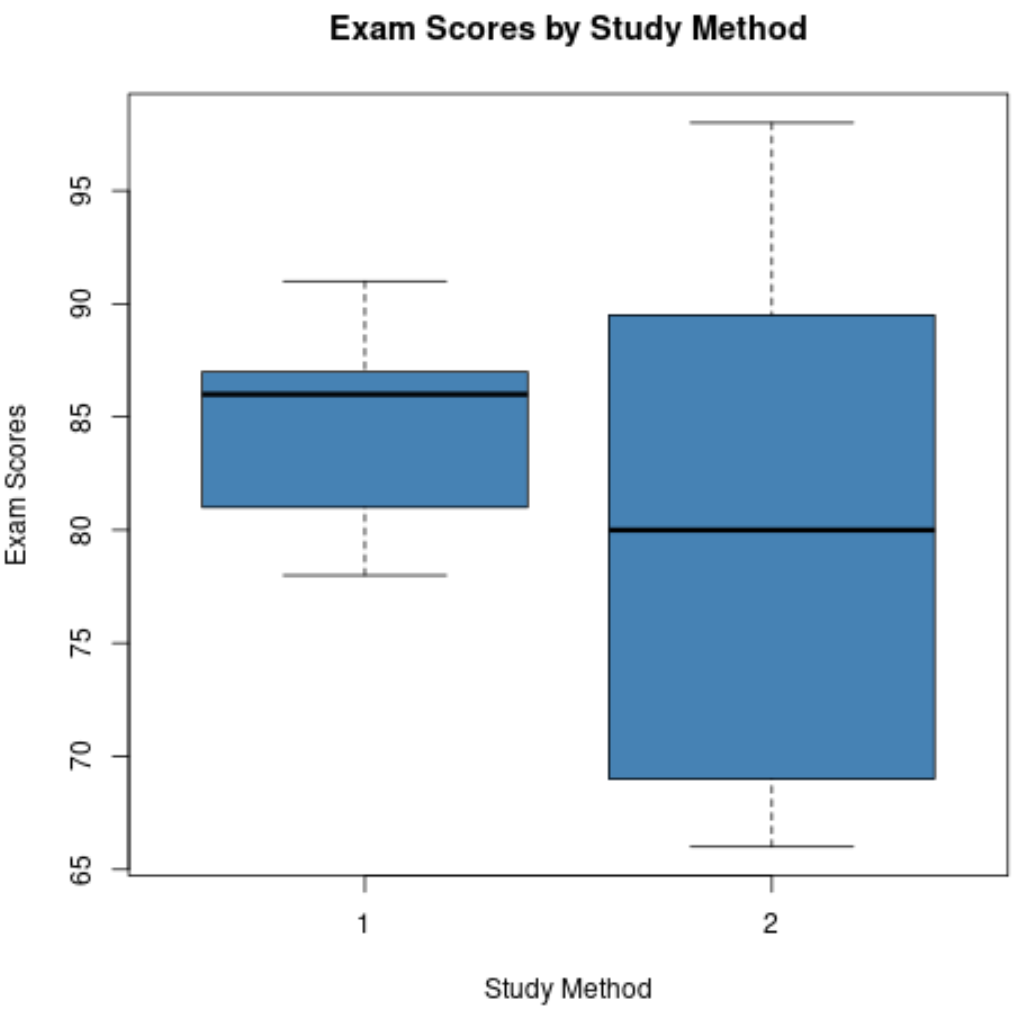
Możemy porównać te dwa wykresy skrzynkowe i odpowiedzieć na następujące cztery pytania:

1. Jak porównują się wartości mediany? Linia pośrodku wykresu pudełkowego dla metody nauki 1 jest wyższa niż linia dla metody nauki 2, co wskazuje, że uczniowie, którzy stosowali metodę nauki 1, uzyskali medianę ocen na wyższym egzaminie.

2. Jak wypada porównanie dyspersji? Wykres pudełkowy dla metody badania 2 jest znacznie dłuższy niż dla metody badania 1, co wskazuje, że wyniki egzaminów są znacznie bardziej rozłożone wśród uczniów, którzy stosowali metodę badania 2.

3. Jak wypada asymetria? Linia pośrodku wykresu pudełkowego dla metody badania 1 jest bliska Q3, co wskazuje, że rozkład wyników egzaminów uczniów, którzy stosowali metodę nauki 1, jest ujemnie wypaczony. I odwrotnie, linia pośrodku wykresu pudełkowego dla metody badania 2 znajduje się blisko środka pudełka, co oznacza, że rozkład wyników jest minimalnie przekrzywiony.

4. Czy występują wartości odstające? Żaden z wykresów pudełkowych nie zawiera małych okręgów wystających poza górne lub dolne wąsy, co oznacza, że w żadnym zestawie danych nie występują wyraźne wartości odstające.

Dodatkowe zasoby

Jak tworzyć i interpretować wykresy pudełkowe w programie Excel
Jak tworzyć i interpretować wykresy pudełkowe w SPSS
Jak utworzyć wiele wykresów pudełkowych w R
Jak tworzyć i interpretować wykresy pudełkowe w Stata