Porównanie wyników z różnych rozkładów

Wynik Z informuje, o ile odchyleń standardowych poszczególne wartości danych spadają od średniej. Oblicza się go w następujący sposób:

wynik z = (x – μ) / σ

Złoto:

• x: indywidualna wartość danych
• μ: średnia populacji
• σ: odchylenie standardowe populacji

Wynik Z dla pojedynczej wartości można interpretować w następujący sposób:

• Dodatni wynik z: indywidualna wartość jest powyżej średniej.
• Ujemny wynik z: indywidualna wartość jest niższa od średniej.
• Wynik z wynoszący 0: indywidualna wartość jest równa średniej.

Wyniki Z są szczególnie przydatne, gdy chcemy porównać względną pozycję dwóch punktów danych z dwóch różnych rozkładów. Aby to zilustrować, rozważmy następujący przykład.

Przykład: porównywanie wyników Z

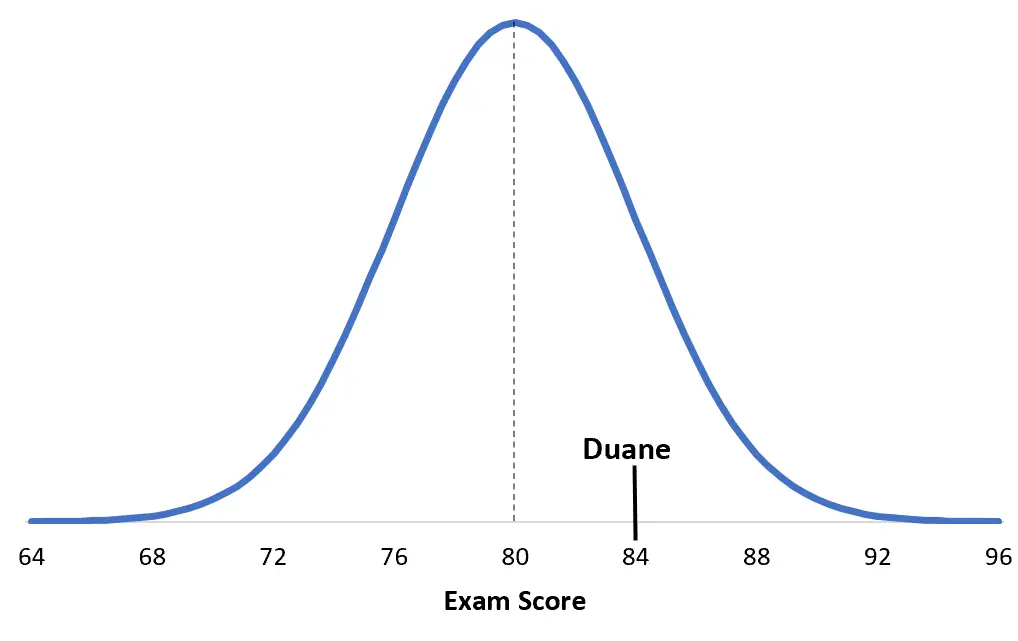
Wyniki niektórych egzaminów uniwersyteckich mają rozkład normalny ze średnią μ = 80 i odchyleniem standardowym σ = 4. Duane uzyskuje na tym egzaminie 84 punkty.

Wyniki innego egzaminu uniwersyteckiego mają rozkład normalny ze średnią μ = 85 i odchyleniem standardowym σ = 8. Debbie otrzymuje na tym egzaminie 90 punktów.

Kto osiągnął najlepsze wyniki na egzaminie w porównaniu z rozkładem wyników egzaminów w ich własnym kraju?

Aby odpowiedzieć na to pytanie, możemy obliczyć wynik Z wyniku egzaminu każdej osoby:

Wynik z Duane’a = (x – μ) / σ = (84 – 80) / 4 = 4 / 4 = 1

Wynik Z Debbie = (x – μ) / σ = (90 – 85) / 8 = 5/8 = 0,625

Debbie Chociaż wynik Duane’a był wyższy, wynik Duane’a jest w rzeczywistości wyższy w porównaniu z rozkładem jego konkretnego egzaminu.

Aby to zrozumieć, warto zwizualizować sytuację. Oto wynik Duane’a w porównaniu z jego konkretnym egzaminem:

A oto wynik Debbie z podsumowania egzaminu:

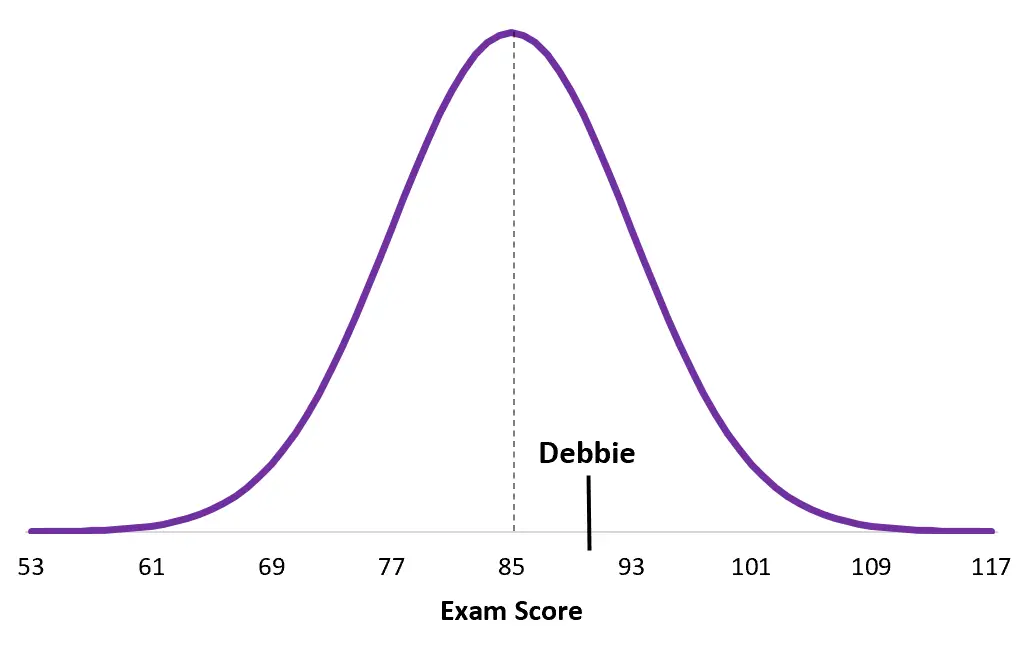
Zwróć uwagę, o ile wynik Debbie jest bliższy średniej jej populacji niż wynik Duane’a. Chociaż ogólnie ma wyższy wynik, jej wynik Z jest niższy po prostu dlatego, że średni wynik na jej konkretnym egzaminie jest wyższy.

Ten przykład ilustruje, dlaczego wyniki Z są tak przydatne do porównywania wartości danych z różnych rozkładów: wyniki Z uwzględniają średnie i odchylenia standardowe rozkładów, co pozwala nam porównać wartości danych z różnych rozkładów i zobaczyć, który jest wyższe w porównaniu z ich własnymi dystrybucjami.

Dodatkowe zasoby

Kalkulator wyniku Z
Porównaj kalkulator wyniku Z