Zrozumienie kształtu rozkładu dwumianowego

Rozkład dwumianowy opisuje prawdopodobieństwo uzyskania k sukcesów w n eksperymentach dwumianowych.

Jeśli zmienna losowa X ma rozkład dwumianowy, prawdopodobieństwo, że X = k powodzenia można obliczyć za pomocą następującego wzoru:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Złoto:

• n: liczba prób
• k: liczba sukcesów
• p: prawdopodobieństwo sukcesu w danej próbie
• _n C _k : liczba sposobów uzyskania k sukcesów w n próbach

Dwumianowy rozkład prawdopodobieństwa ma zwykle kształt dzwonu, gdy zachodzi jeden lub więcej z następujących dwóch warunków:

1. Wielkość próby (n) jest duża.

2. Prawdopodobieństwo powodzenia danej próby (p) jest bliskie 0,5.

Jednakże dwumianowy rozkład prawdopodobieństwa jest zwykle wypaczony, gdy nie występuje żaden z tych warunków. Aby to zilustrować, rozważ następujące przykłady:

Przykład 1: Wielkość próby (n) jest duża

Poniższy wykres przedstawia rozkład prawdopodobieństwa, gdy n = 200 i p = 0,5 .

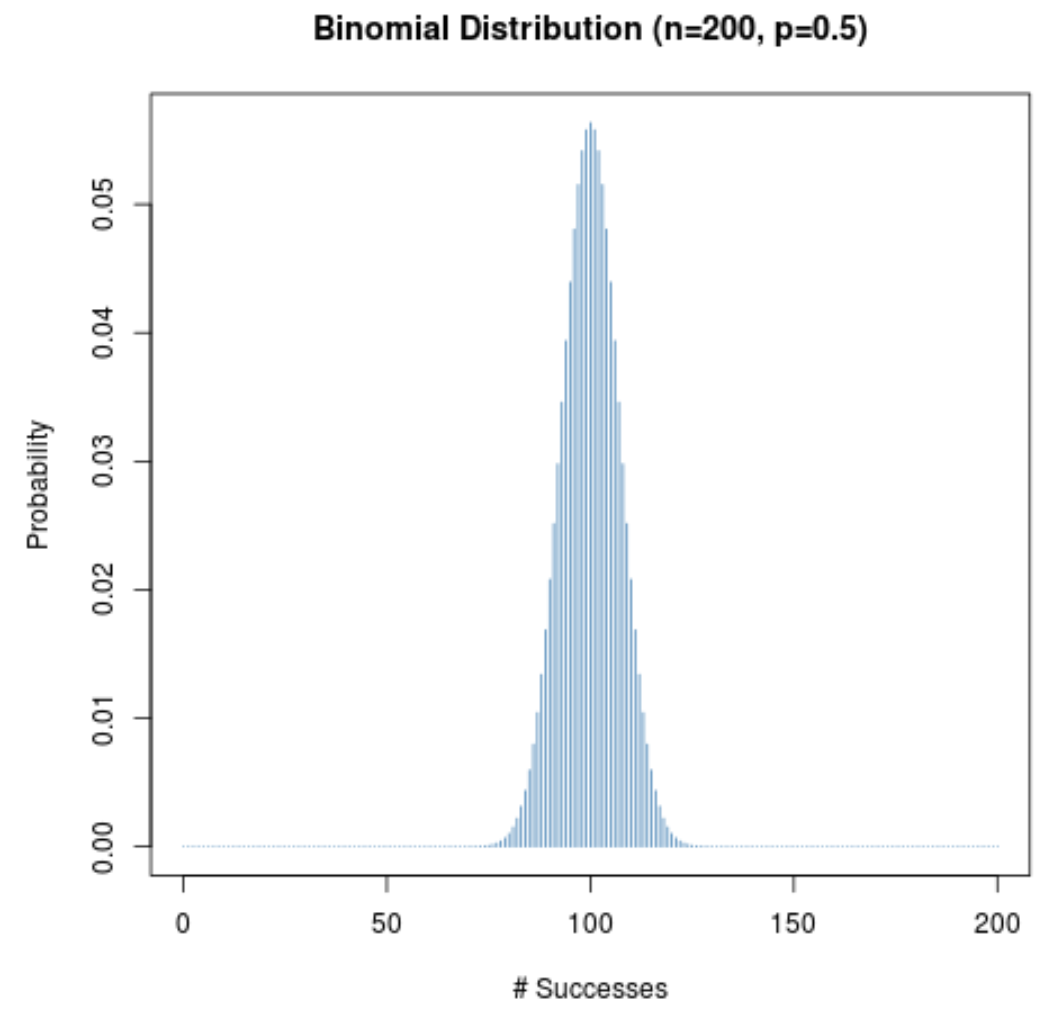
Oś x przedstawia liczbę sukcesów w 200 próbach, a oś y przedstawia prawdopodobieństwo wystąpienia tej liczby sukcesów.

Ponieważ (1) wielkość próby jest duża oraz (2) prawdopodobieństwo powodzenia danej próby jest bliskie 0,5, rozkład prawdopodobieństwa ma kształt dzwonu.

Nawet jeśli prawdopodobieństwo powodzenia danej próby (p) nie jest bliskie 0,5, rozkład prawdopodobieństwa będzie miał kształt dzwonu, dopóki wielkość próby (n) będzie duża. Aby to zilustrować, rozważmy następujące dwa scenariusze, gdy p = 0,2 i p = 0,8.

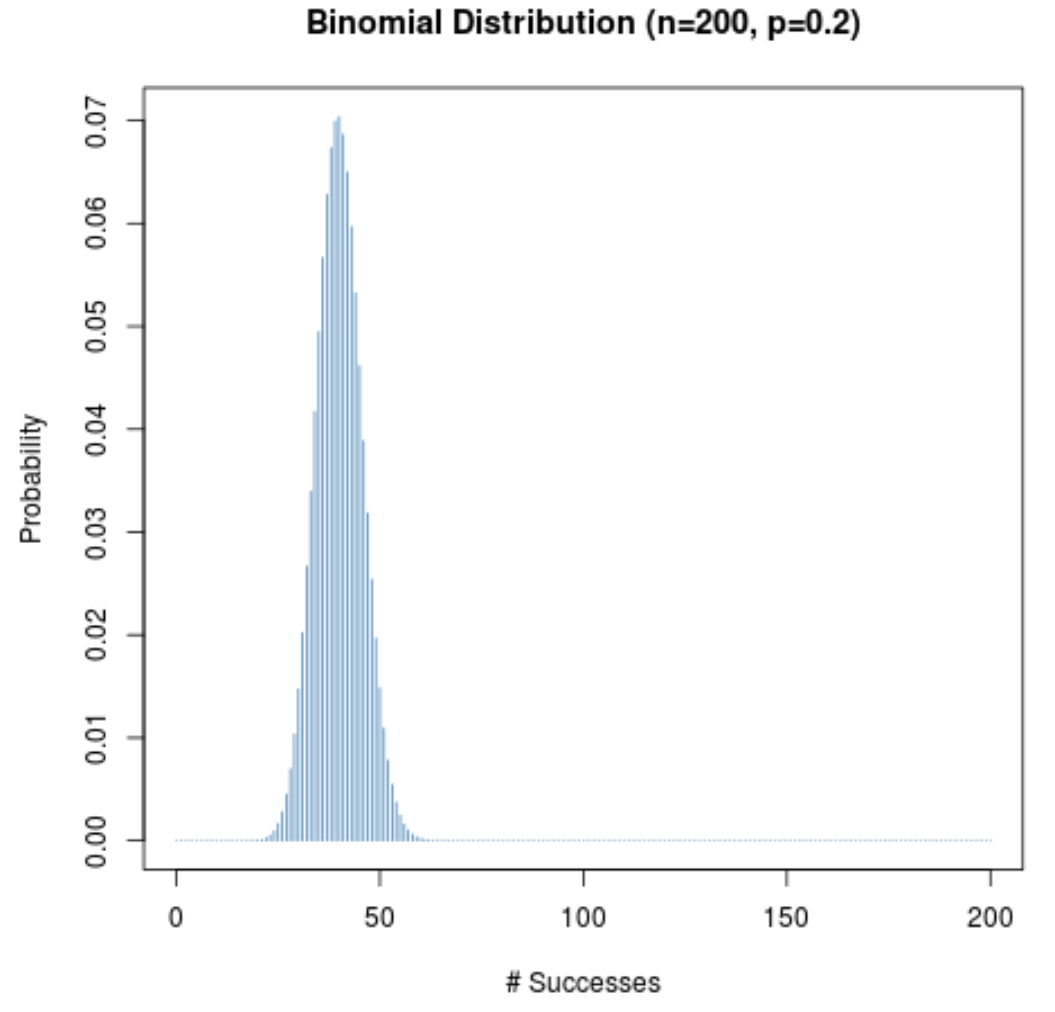
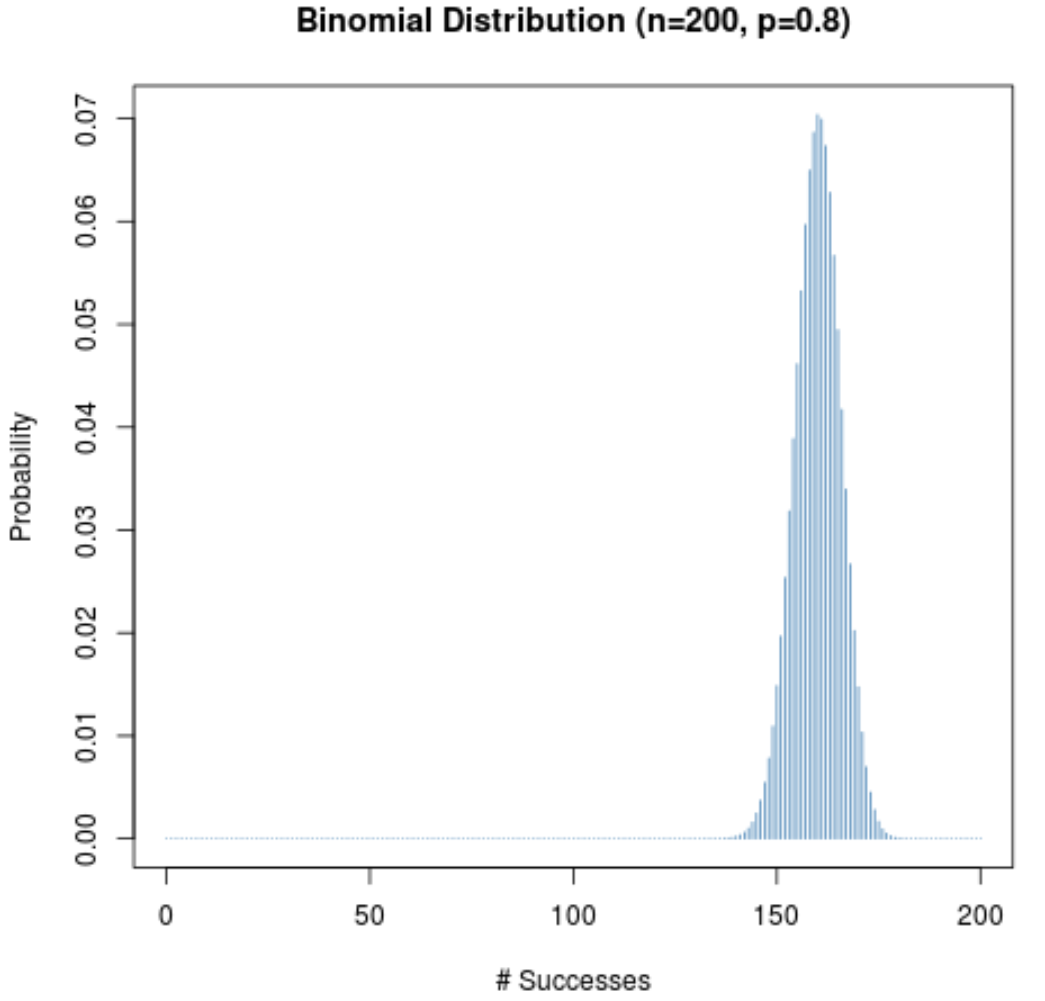
Zwróć uwagę, że w obu scenariuszach rozkład prawdopodobieństwa ma kształt dzwonu.

Przykład 2: prawdopodobieństwo sukcesu (p) jest bliskie 0,5

Poniższy wykres przedstawia rozkład prawdopodobieństwa, gdy n = 10 i p = 0,4 .

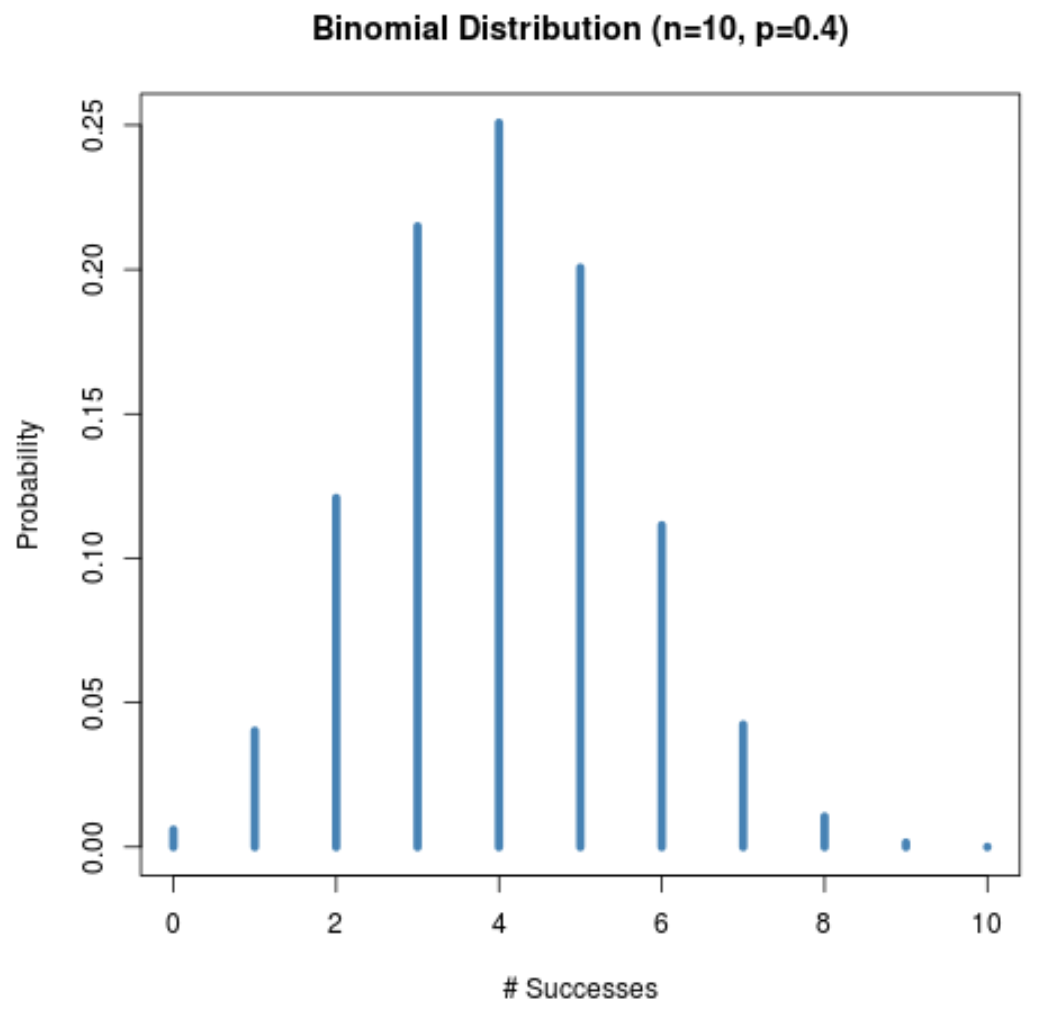
Mimo że liczebność próby (n = 10) jest niewielka, rozkład prawdopodobieństwa pozostaje w kształcie dzwonu, ponieważ prawdopodobieństwo powodzenia danej próby (p = 0,4) jest bliskie 0,5.

Przykład 3: Skośne rozkłady dwumianowe

Jeżeli ani (1) wielkość próby nie jest duża, ani (2) prawdopodobieństwo powodzenia danej próby nie jest bliskie 0,5, dwumianowy rozkład prawdopodobieństwa będzie przesunięty w lewo lub w prawo.

Na przykład poniższy wykres przedstawia rozkład prawdopodobieństwa, gdy n = 20 i p = 0,1 .

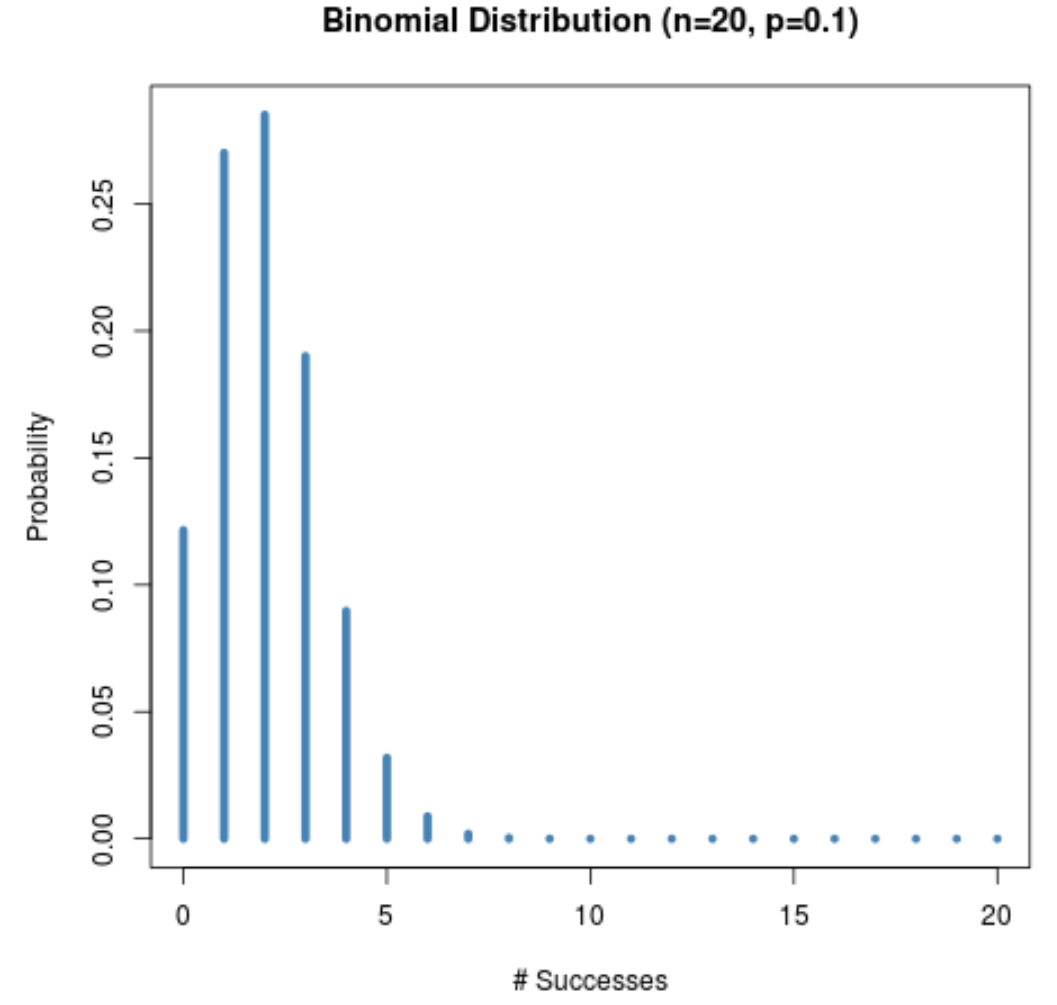
Zwróć uwagę, jak rozkład jest przesunięty w prawo.

Poniższy wykres przedstawia rozkład prawdopodobieństwa, gdy n = 20 i p = 0,9 .

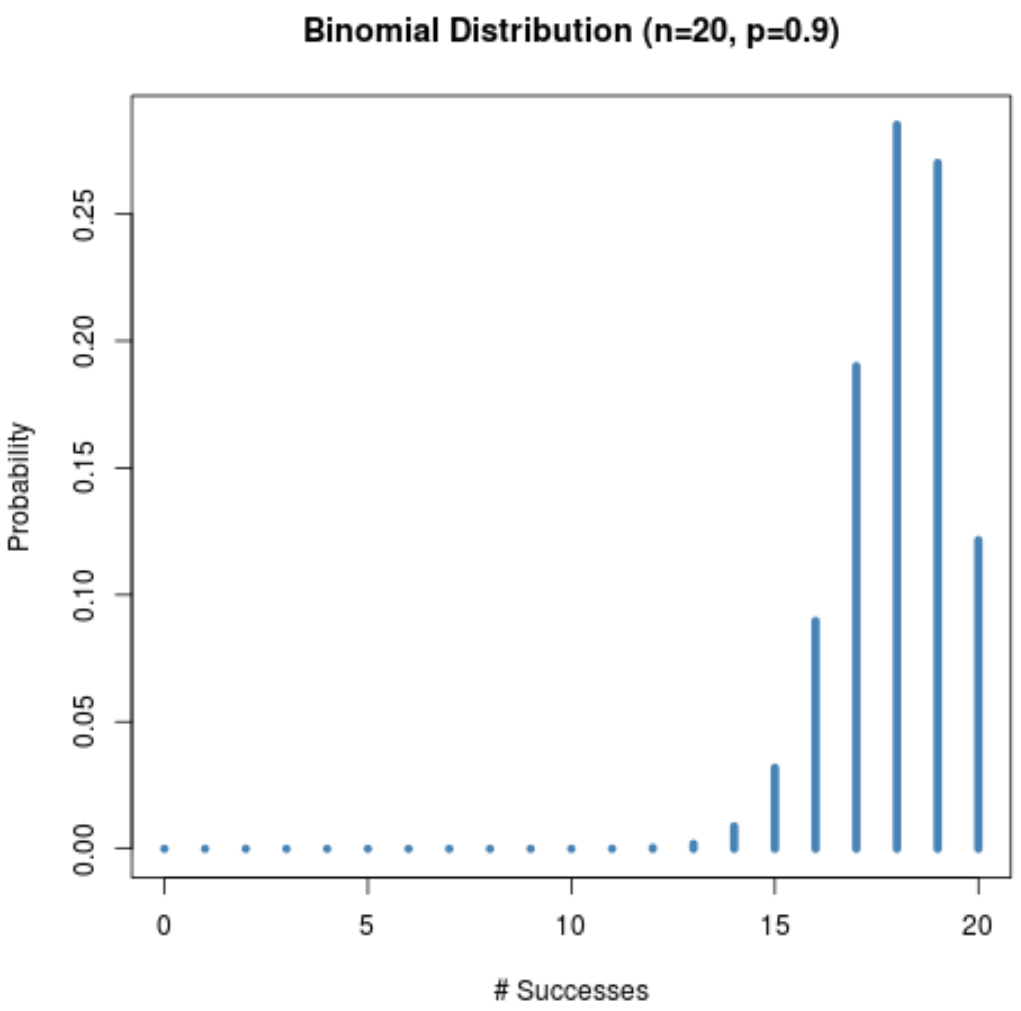
Zwróć uwagę, jak rozkład jest przesunięty w lewo.

Przypisy końcowe

Każdy z wykresów w tym artykule został utworzony przy użyciu statystycznego języka programowania R. Korzystając z tego samouczka, dowiesz się, jak wykreślić własne dwumianowe rozkłady prawdopodobieństwa w języku R.