Jak wykonywać powtarzane pomiary anova w spss

ANOVA z powtarzanymi pomiarami służy do określenia, czy istnieje statystycznie istotna różnica pomiędzy średnimi z trzech lub więcej grup, w których w każdej grupie pojawiają się ci sami pacjenci.

W tym samouczku wyjaśniono, jak wykonać jednokierunkową ANOVA z powtarzanymi pomiarami w SPSS.

Przykład: ANOVA z powtarzanymi pomiarami w SPSS

Naukowcy chcą wiedzieć, czy cztery różne leki powodują różne czasy reakcji. Aby to sprawdzić, zmierzyli czas reakcji pięciu pacjentów na cztery różne leki. Ponieważ u każdego pacjenta badany jest każdy z czterech leków, zastosujemy ANOVA z powtarzanymi pomiarami, aby określić, czy średni czas reakcji różni się w zależności od leku.

Wykonaj poniższe kroki, aby wykonać powtarzane pomiary ANOVA w SPSS.

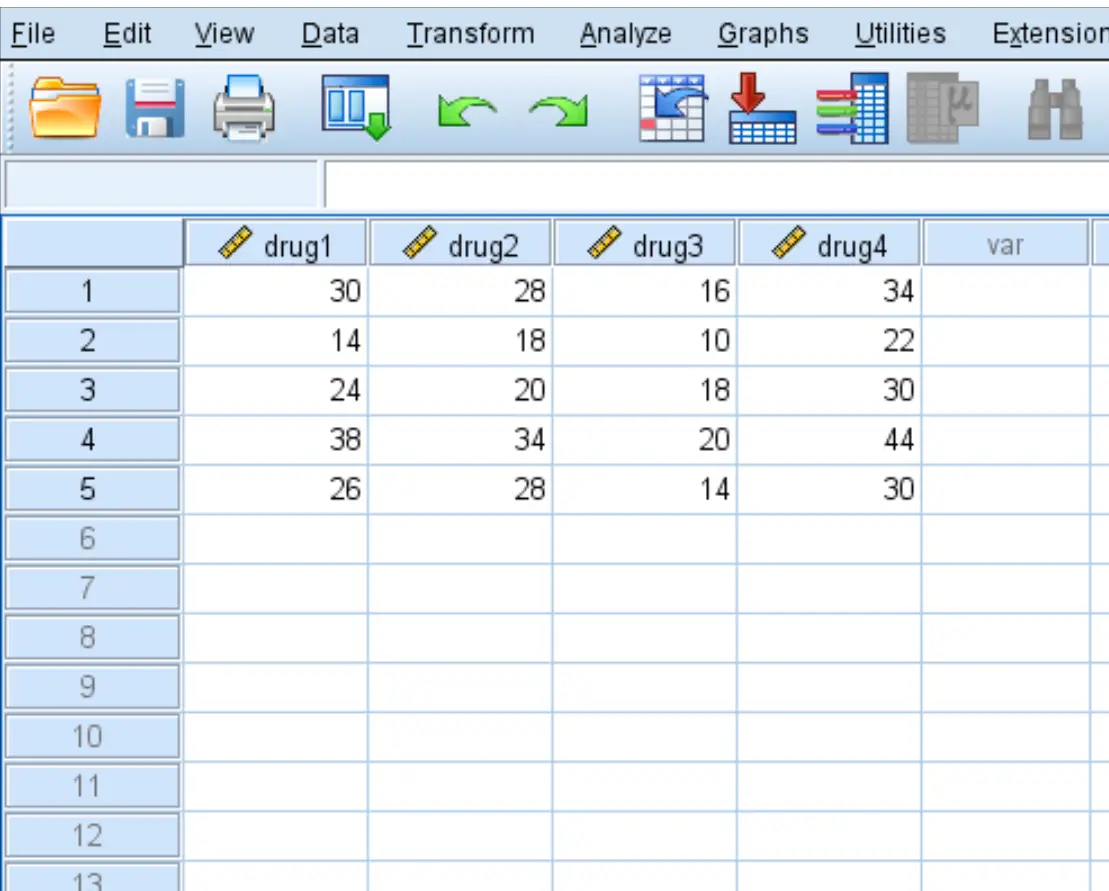
Krok 1: Wprowadź dane.

Wprowadź następujące dane, które pokazują czas reakcji (w sekundach) pięciu pacjentów na cztery leki:

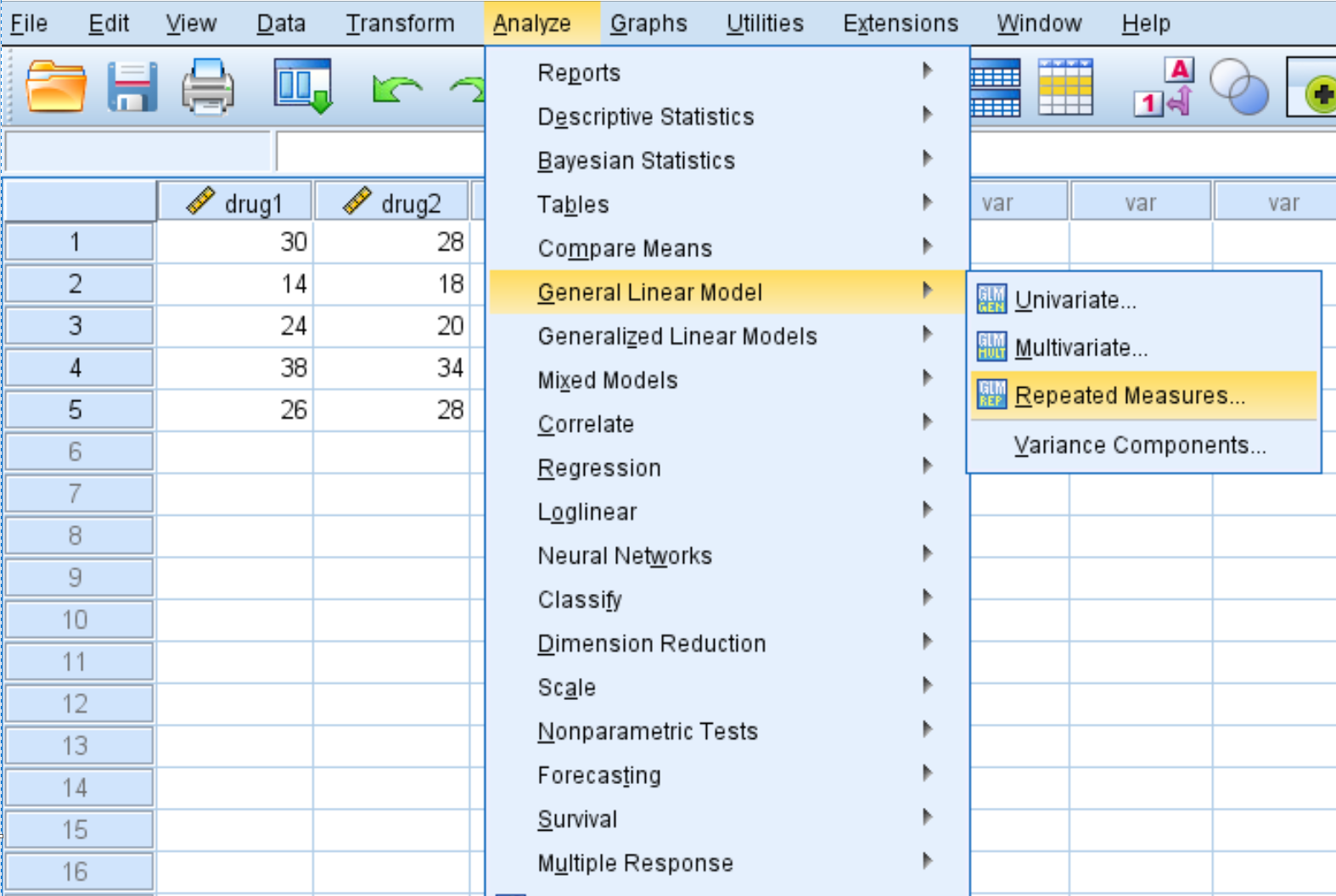
Krok 2: Wykonaj powtarzane pomiary ANOVA.

Kliknij kartę Analiza , następnie Ogólny model liniowy , a następnie Pomiary powtarzane :

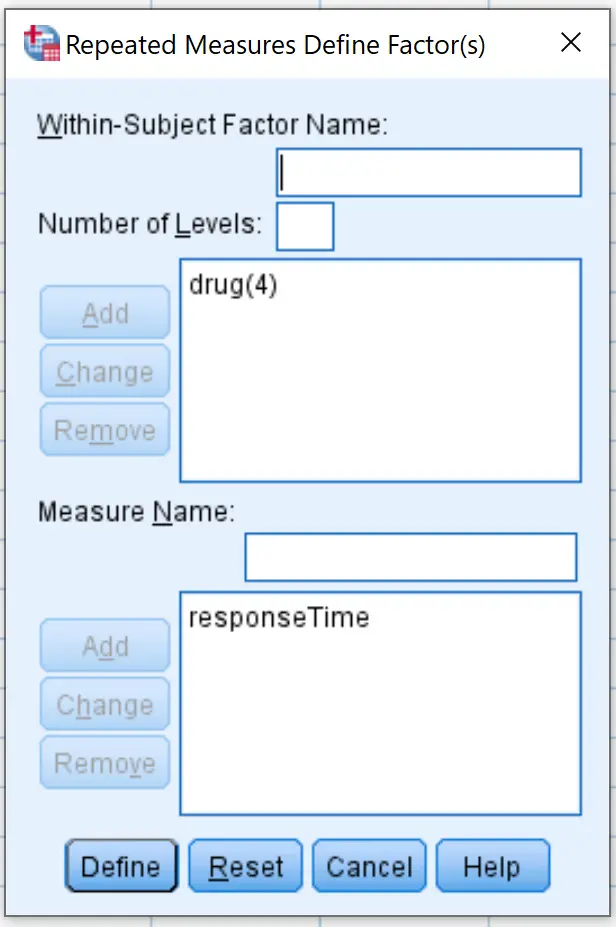
W nowym oknie, które się pojawi, wpisz lek jako nazwę czynnika wewnątrzosobniczego. Wpisz 4 jako liczbę poziomów (ponieważ każdy uczestnik badania testował 4 różne leki), a następnie kliknij Dodaj . Wpisz Czas odpowiedzi w polu Nazwa miary , a następnie kliknij przycisk Dodaj . Na koniec kliknij Ustaw .

W nowym oknie, które się pojawi, przeciągnij każdą z czterech zmiennych dotyczących leku do obszaru oznaczonego jako Zmienne wewnątrzobiektowe :

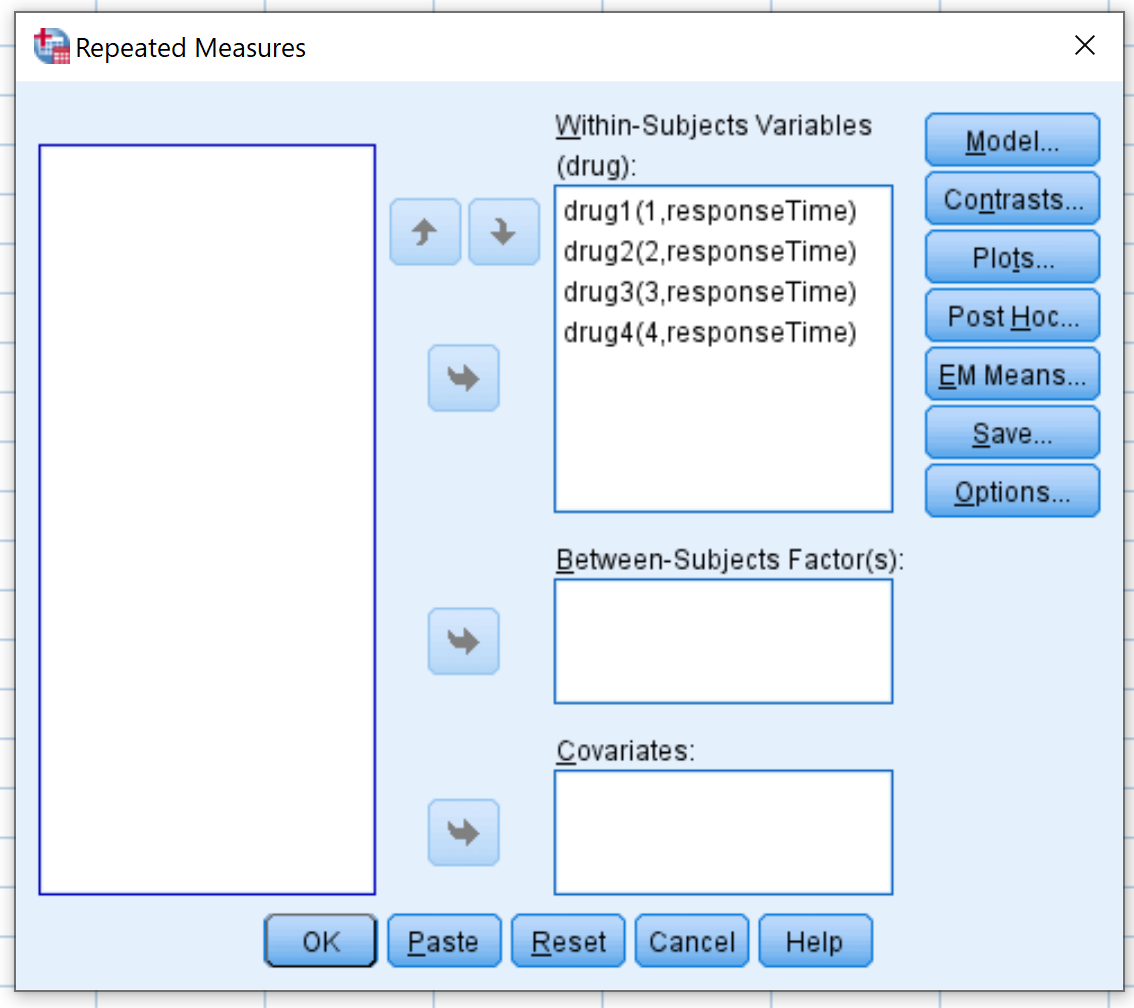
Następnie kliknij Wykresy . Przeciągnij zmienny lek do obszaru oznaczonego Oś pozioma . Następnie kliknij Dodaj . Następnie kliknij Kontynuuj .

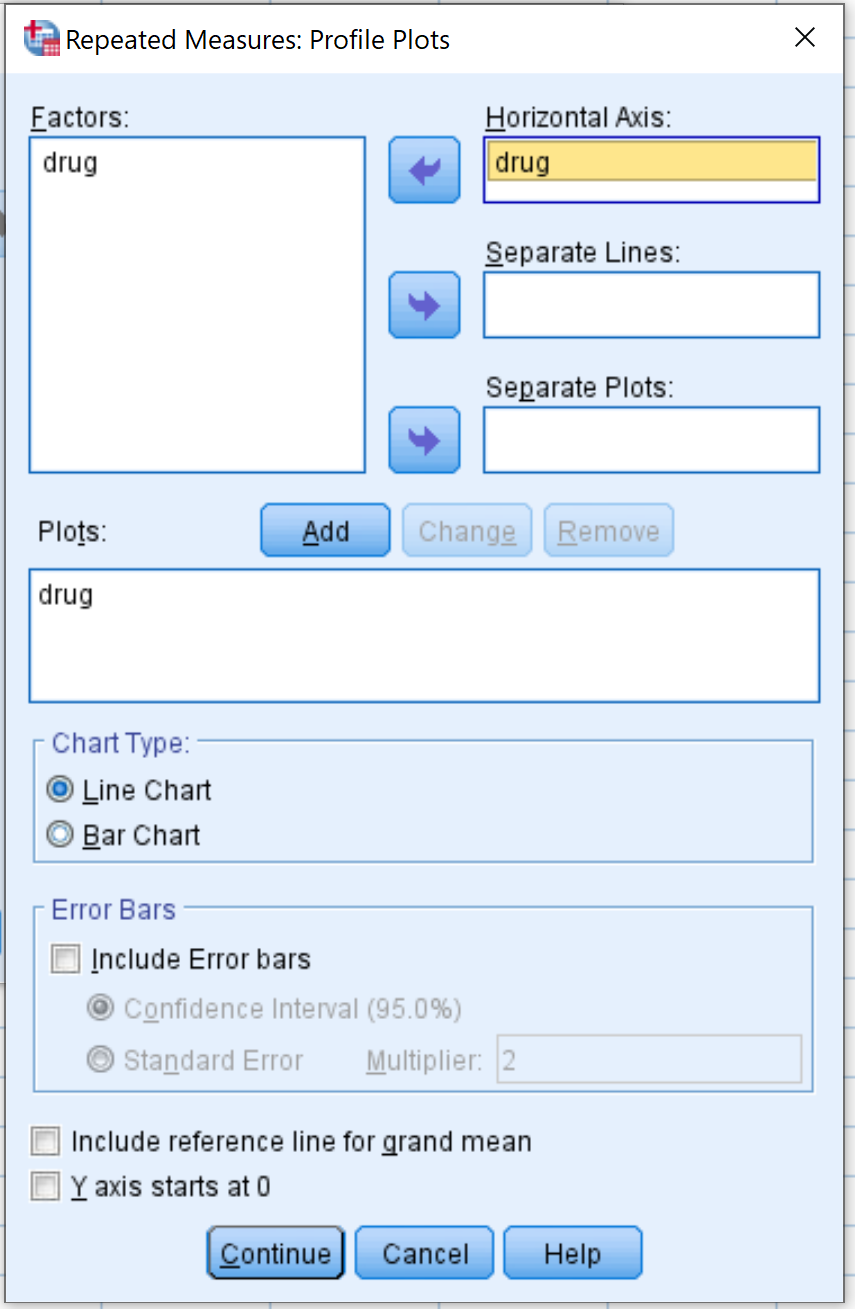
Następnie kliknij opcję EM Means . Przeciągnij zmienną leku do pola oznaczonego Pokaż środki dla . Następnie zaznacz pole obok Porównaj efekty główne i wybierz Bonferroni z rozwijanego menu. Następnie kliknij Kontynuuj .

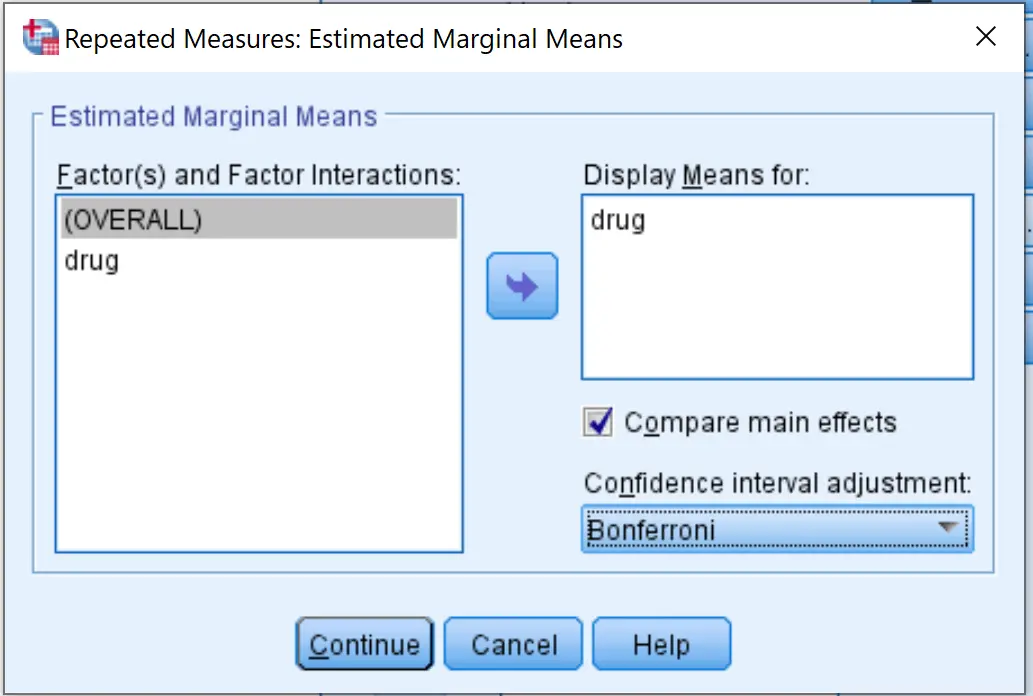
Na koniec kliknij OK .

Krok 2: Interpretacja wyników.

Po kliknięciu OK pojawią się wyniki powtarzanych pomiarów ANOVA. Oto jak zinterpretować wynik:

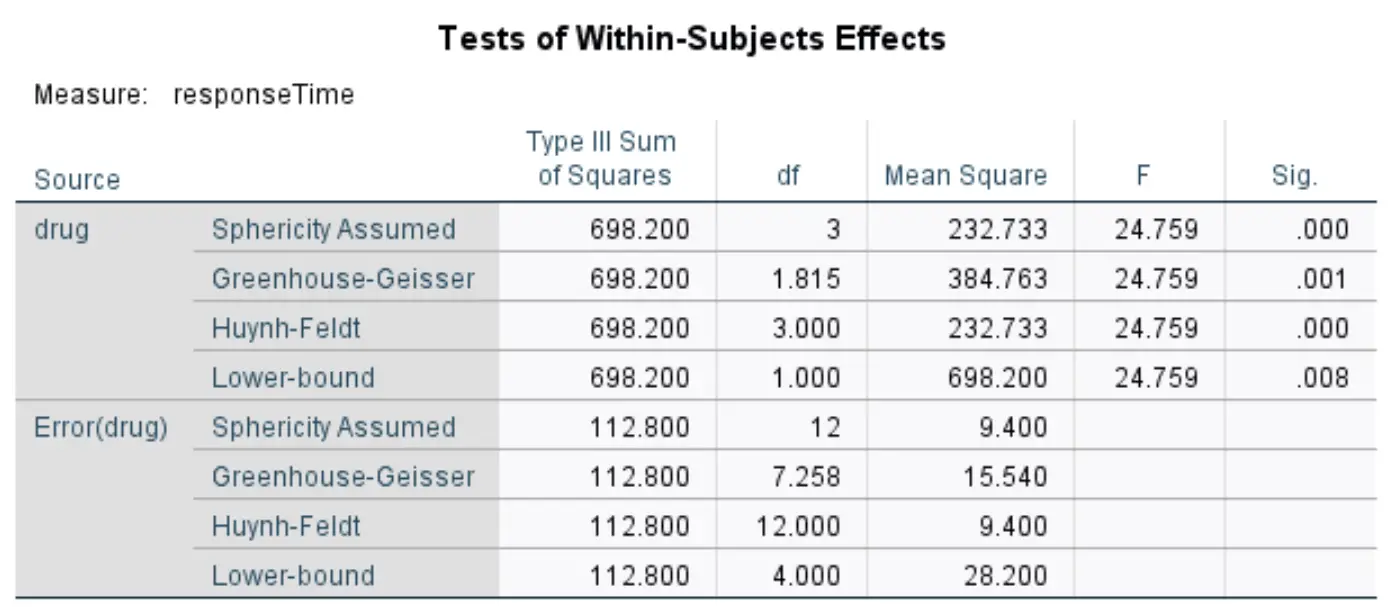
Testy efektów wewnątrzobiektowych

Ta tabela przedstawia ogólną statystykę F i odpowiadającą jej wartość p z powtarzanych pomiarów ANOVA. Zwykle używamy wartości z linii oznaczonej Greenhouse-Geisser .

Zgodnie z tą linią statystyka F wynosi 24,759 , a odpowiadająca jej wartość p wynosi 0,001 . Ponieważ ta wartość p jest mniejsza niż 0,05, możemy odrzucić hipotezę zerową i stwierdzić, że istnieje statystycznie istotna różnica w średnim czasie reakcji pomiędzy czterema lekami.

Porównania parami

Ponieważ odrzuciliśmy hipotezę zerową, oznacza to, że co najmniej dwie średnie grupowe są różne. Aby określić, które grupy średnich są różne, możemy skorzystać z tabeli, która przedstawia porównania parami pomiędzy każdym lekiem.

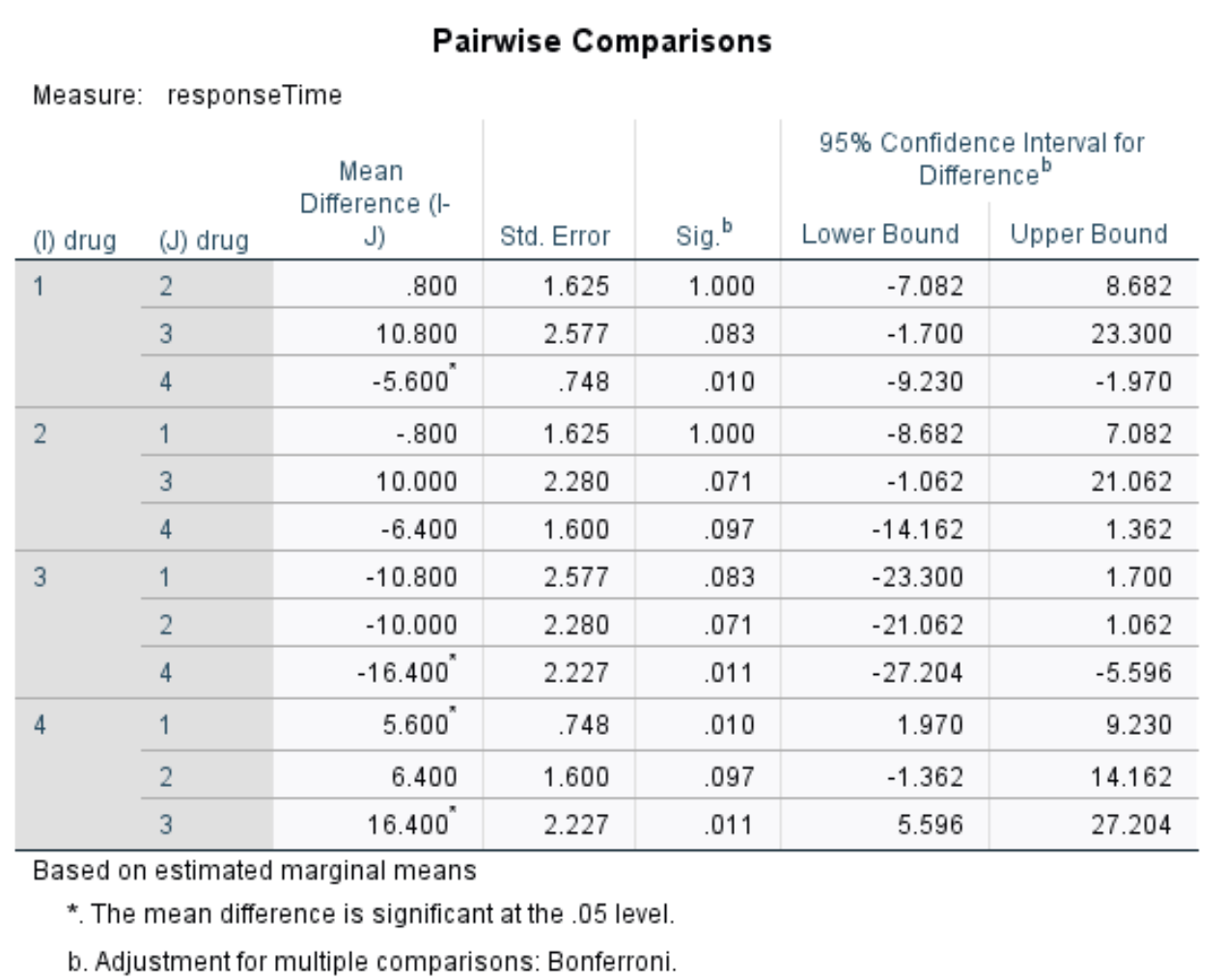
W tabeli możemy zobaczyć wartości p dla następujących porównań:

• lek 1 kontra lek 2 | wartość p = 1,000
• lek 1 kontra lek 3 | wartość p = 0,083
• lek 1 kontra lek 4 | wartość p = 0,010
• lek 2 kontra lek 3 | wartość p = 0,071
• lek 2 kontra lek 4 | wartość p = 0,097
• lek 3 kontra lek 4 | wartość p = 0,011

Jedyne wartości p mniejsze niż 0,05 dotyczą leku 1 w porównaniu z lekiem 4 i leku 3 w porównaniu z lekiem 4. Wszystkie inne porównania mają wartości p większe niż 0,05.

Wykres szacunkowych średnich krańcowych

Na tym wykresie przedstawiono szacowany średni czas reakcji na każdy lek. Z wykresu wyraźnie widać, że czasy reakcji różniły się znacząco pomiędzy czterema różnymi lekami:

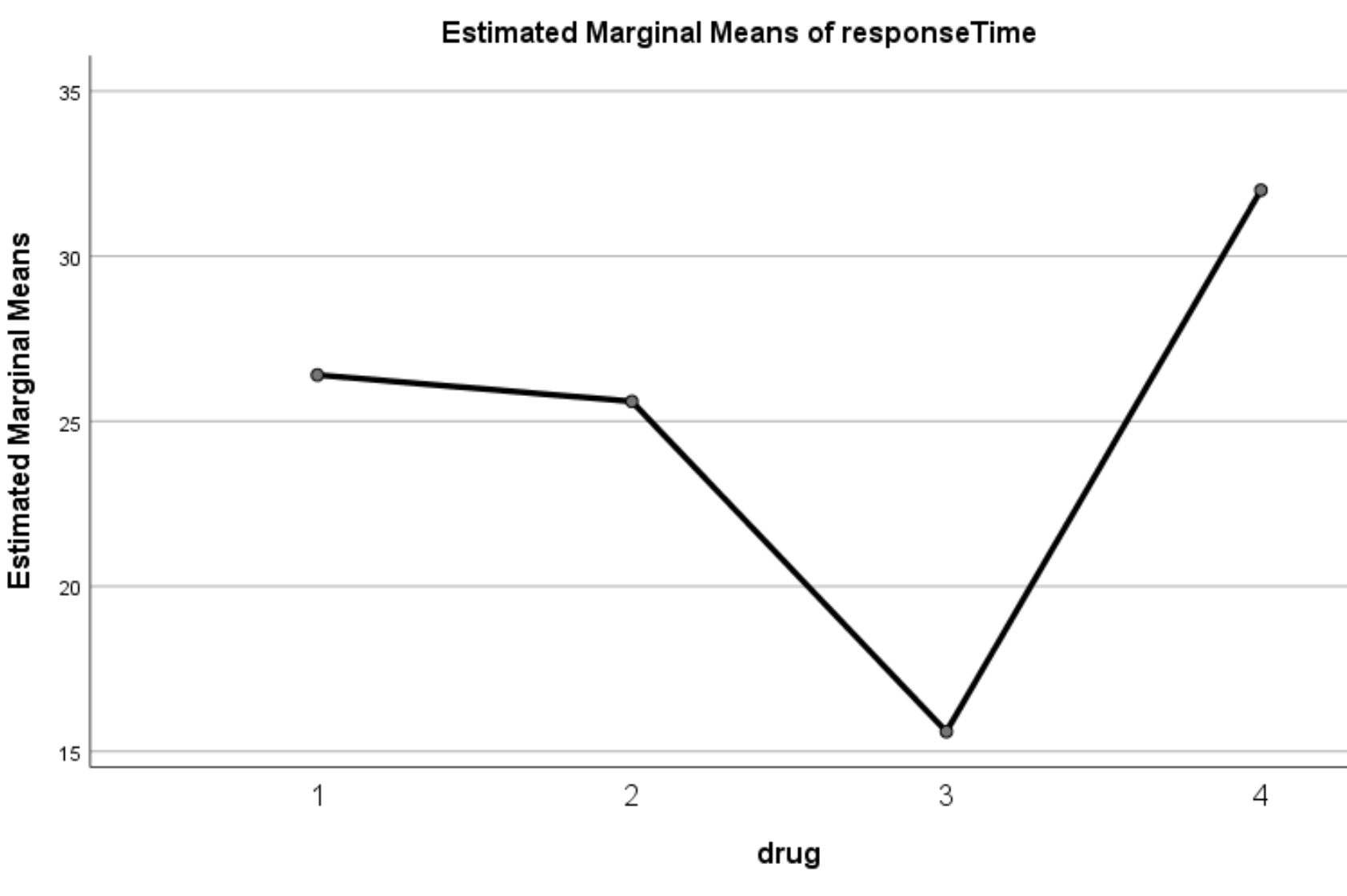
Krok 3: Ogłoś wyniki.

Na koniec możemy zgłosić wyniki powtarzanych pomiarów ANOVA. Oto przykład, jak to zrobić:

Przeprowadzono jednoczynnikową analizę ANOVA z powtarzanymi pomiarami, aby określić, czy średni czas reakcji pacjentów różnił się w przypadku czterech różnych leków.

Jednokierunkowa ANOVA z powtarzanymi pomiarami ujawniła, że rodzaj stosowanego leku spowodował statystycznie istotne różnice w czasie odpowiedzi (F = 24,75887, p = 0,001).

Test Bonferroniego do porównań wielokrotnych wykazał statystycznie istotną różnicę w czasie odpowiedzi pomiędzy pacjentami przyjmującymi lek 1 i lek 4 oraz lek 3 i lek 4.