Trzy założenia anova powtarzanych pomiarów

ANOVA z powtarzanymi pomiarami służy do określenia, czy istnieje statystycznie istotna różnica pomiędzy średnimi z trzech lub więcej grup, w których w każdej grupie pojawiają się ci sami pacjenci.

Jednakże przed wykonaniem powtarzanych pomiarów ANOVA musimy upewnić się, że spełnione są następujące założenia:

1. Niezależność: Każda obserwacja musi być niezależna.

2. Normalność: Rozkład zmiennej odpowiedzi ma rozkład normalny.

3. Sferyczność: wariancje różnic pomiędzy wszystkimi kombinacjami powiązanych grup muszą być równe.

Jeśli jedno lub więcej z tych założeń zostanie naruszonych, wyniki ANOVA z powtarzanymi pomiarami mogą być niewiarygodne.

W tym artykule wyjaśniamy każde założenie, wyjaśniamy, jak ustalić, czy założenie jest spełnione i co zrobić, jeśli nie jest spełnione.

Hipoteza 1: Niepodległość

Powtarzane pomiary ANOVA zakładają, że każda obserwacja w zestawie danych jest niezależna od wszystkich innych obserwacji.

Jak ustalić, czy to założenie jest spełnione

Najprostszym sposobem sprawdzenia tego założenia jest sprawdzenie, czy każda osoba w zbiorze danych została wybrana losowo z populacji przy użyciu metody losowego doboru próby .

Jeżeli zastosowano metodę losowego doboru próby, można założyć, że każda obserwacja jest niezależna.

Co zrobić, jeśli to założenie nie jest przestrzegane

Jeśli to założenie nie jest spełnione, jest to poważny problem, ponieważ wartości każdej jednostki mogą być ze sobą w taki czy inny sposób powiązane.

Często jedynym rozwiązaniem w tym scenariuszu jest rekrutacja osób do nowego badania przy użyciu metody losowego doboru próby.

Hipoteza 2: normalność

Powtarzane pomiary ANOVA zakładają, że rozkładzmiennej odpowiedzi ma rozkład normalny .

Jak ustalić, czy to założenie jest spełnione

Prawdziwość tej hipotezy można sprawdzić na dwa sposoby:

1. Utwórz histogram lub wykres QQ

Można wizualnie sprawdzić, czy rozkład zmiennej odpowiedzi ma w przybliżeniu rozkład normalny, tworząc histogram lub wykres QQ.

Jeśli utworzysz histogram , po prostu sprawdź, czy rozkład zmiennej odpowiedzi ma w przybliżeniu kształt „dzwonka”. Jeśli tak, często można założyć, że założenie normalności jest spełnione:

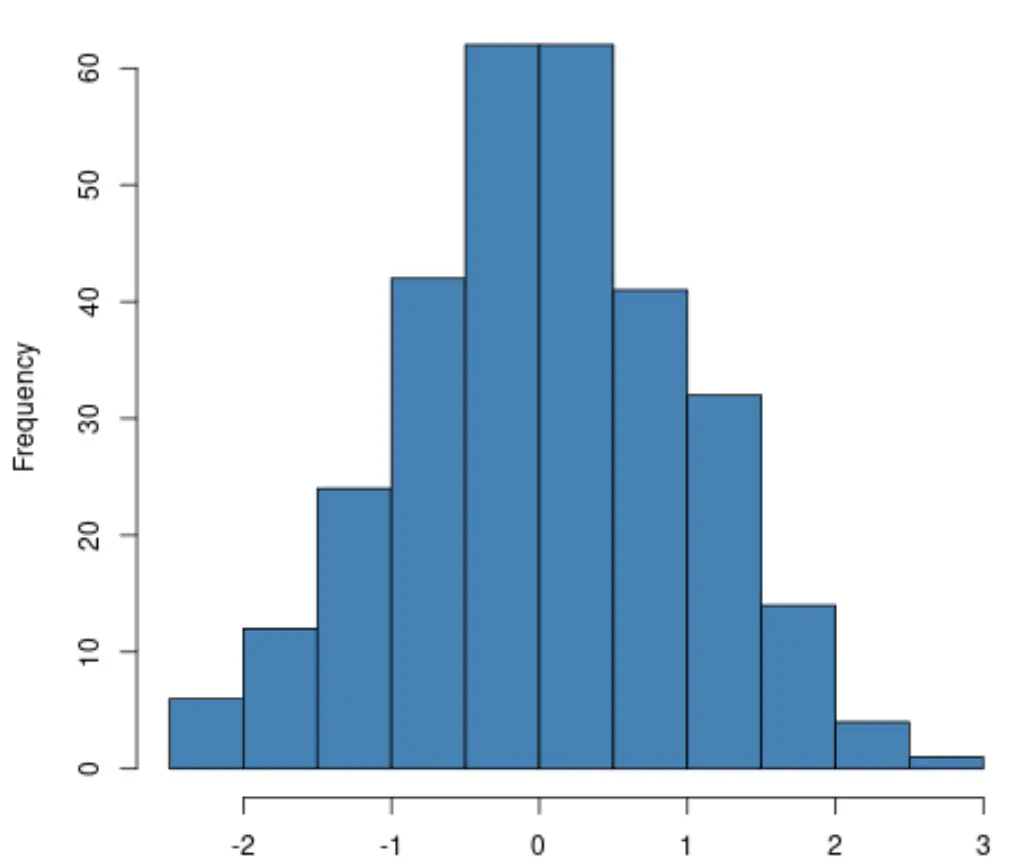
Jeśli tworzysz wykres QQ , sprawdź, czy punkty danych leżą wzdłuż prostej linii ukośnej. Jeśli tak, można ogólnie założyć, że założenie normalności jest spełnione:

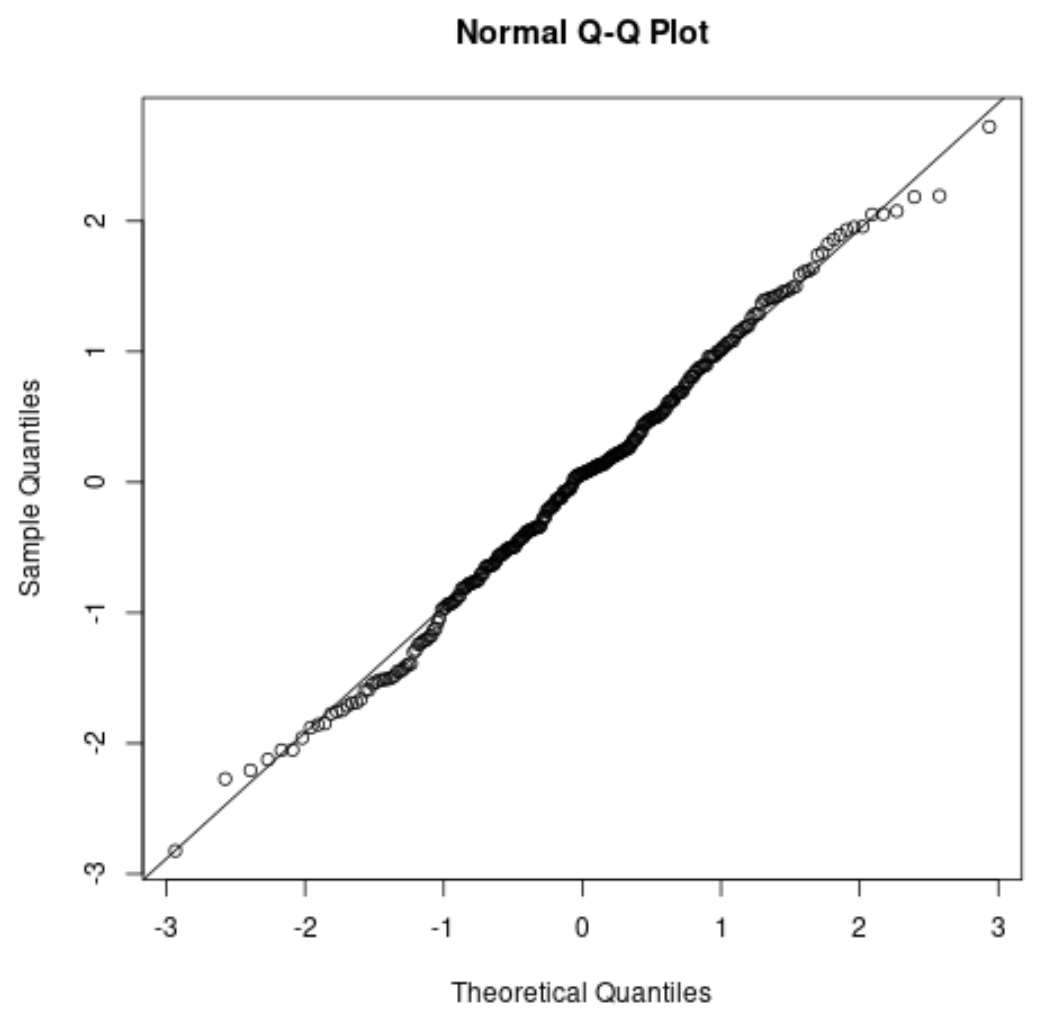
Powiązane: Jak używać wykresów QQ do sprawdzania normalności

2. Wykonaj formalny test statystyczny

Możesz także wykonać test Shapiro-Wilka, aby sprawdzić normalność. Jeśli wartość p testu jest mniejsza niż 0,05, sugeruje to, że dane nie mają rozkładu normalnego.

Należy jednak pamiętać, że podczas pracy z bardzo dużymi próbami testy statystyczne, takie jak test Shapiro-Wilka, prawie zawsze wykażą, że dane nie są normalne.

Z tego powodu często najlepiej jest wizualnie sprawdzić dane za pomocą wykresów, takich jak histogramy i wykresy QQ. Wystarczy spojrzeć na wykresy, aby uzyskać całkiem niezłe pojęcie o tym, czy dane mają rozkład normalny, czy nie.

Co zrobić, jeśli to założenie nie jest przestrzegane

Ogólnie rzecz biorąc, ANOVA z powtarzanymi pomiarami jest uważana za dość odporną na naruszenia założenia normalności, o ile rozmiary próbek są wystarczająco duże.

Jeśli założenie o normalności zostanie poważnie naruszone, masz dwie możliwości:

1. Przekształć wartości odpowiedzi swoich danych, aby rozkłady były bardziej normalne.

2. Wykonaj równoważny test nieparametryczny, taki jak test Friedmana , który nie wymaga założenia normalności.

Założenie 3: Sferyczność

ANOVA z powtarzanymi pomiarami zakłada sferyczność – to znaczy wariancje różnic pomiędzy wszystkimi kombinacjami powiązanych grup muszą być równe.

Jeśli to założenie nie zostanie spełnione, współczynnik F zostanie zawyżony, a wyniki powtarzanych pomiarów ANOVA staną się niewiarygodne.

Jak ustalić, czy to założenie jest spełnione

Aby sprawdzić, czy założenie to jest spełnione, możemy przeprowadzić test sferyczności Mauchly’ego.

W teście tym wykorzystuje się następującą hipotezę zerową i alternatywną:

• H ₀ : Wariancje różnic są równe
• H _A : Wariancje różnic nie są równe

Jeżeli wartość p testu jest poniżej pewnego poziomu istotności (np. α = 0,05), wówczas odrzucamy hipotezę zerową i stwierdzamy, że wariancje różnic nie są równe.

W przeciwnym razie, jeśli wartość p jest nie mniejsza niż pewien poziom istotności (np. α = 0,05), nie odrzucamy hipotezy zerowej i nie stwierdzamy, że założenie o kulistości jest spełnione.

W zależności od używanego oprogramowania statystycznego wyniki tego testu będą wyglądać następująco:

Ponieważ wartość p jest nie mniejsza niż 0,05, nie odrzucimy hipotezy zerowej i nie dojdziemy do wniosku, że w tym konkretnym przykładzie spełnione jest założenie o kulistości.

Co zrobić, jeśli to założenie nie jest przestrzegane

Jeśli odrzucimy hipotezę zerową testu sferyczności Mauchly’ego, generalnie stosujemy korektę do stopni swobody użytych do obliczenia wartości F w tabeli ANOVA z powtarzanymi pomiarami.

Możemy zastosować trzy poprawki:

• Huynh-Feldt (najmniej konserwatywny)
• Serre-Geisser
• Dolny limit (najbardziej konserwatywny)

Każda z tych poprawek ma tendencję do zwiększania wartości p w tabeli wyjściowej ANOVA powtarzanych pomiarów, aby uwzględnić fakt, że naruszone zostało założenie o kulistości.

Możemy następnie użyć tych wartości p, aby określić, czy powinniśmy odrzucić hipotezę zerową ANOVA z powtarzanymi pomiarami.

Dodatkowe zasoby

Poniższe tutoriale dostarczają dodatkowych informacji na temat ANOVA z powtarzanymi pomiarami:

Wprowadzenie do powtarzanych pomiarów ANOVA
Kalkulator ANOVA powtarzanych pomiarów
Jak zgłosić wyniki powtarzanych pomiarów ANOVA
Jednokierunkowa ANOVA i ANOVA z powtarzanymi pomiarami: różnica