Co to jest poziom beta w statystykach? (definicja – przykład)
W statystyce testujemy hipotezy , aby określić, czy hipoteza dotycząca parametru populacji jest prawdziwa.
Testowanie hipotez zawsze składa się z dwóch następujących hipotez:
Hipoteza zerowa (H 0 ): Dane z próby są zgodne z dominującym przekonaniem dotyczącym parametru populacji.
Hipoteza alternatywna ( HA ): Przykładowe dane sugerują, że hipoteza zawarta w hipotezie zerowej nie jest prawdziwa. Innymi słowy, na dane ma wpływ przyczyna nieprzypadkowa.
Ilekroć przeprowadzamy test hipotezy, zawsze istnieją cztery możliwe wyniki:
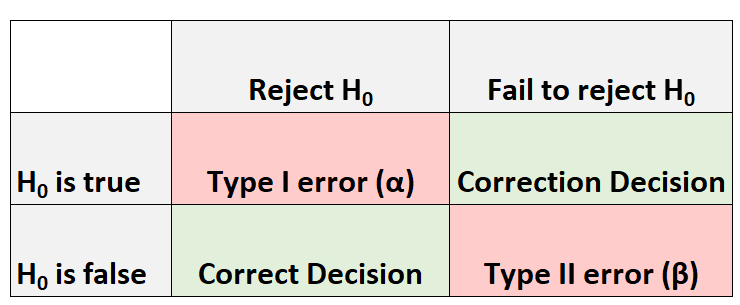
Istnieją dwa rodzaje błędów, które możemy popełnić:
- Błąd pierwszego rodzaju: Odrzucamy hipotezę zerową, jeśli jest ona rzeczywiście prawdziwa. Prawdopodobieństwo popełnienia tego rodzaju błędu oznacza się α .
- Błąd typu II: Nie odrzucamy hipotezy zerowej, gdy jest ona w rzeczywistości fałszywa. Prawdopodobieństwo popełnienia tego rodzaju błędu jest odnotowywane jako β .
Związek między alfa i beta
Idealnie byłoby, gdyby badacze chcieli, aby prawdopodobieństwo popełnienia błędu I rodzaju i prawdopodobieństwo popełnienia błędu II rodzaju było niskie.
Istnieje jednak kompromis pomiędzy tymi dwoma prawdopodobieństwami. Jeśli obniżymy poziom alfa, możemy zmniejszyć prawdopodobieństwo odrzucenia hipotezy zerowej, gdy jest ona rzeczywiście prawdziwa, ale w rzeczywistości zwiększa to poziom beta – prawdopodobieństwo, że nie odrzucimy hipotezy zerowej, gdy jest ona błędna.
Związek między mocą a beta
Moc testu hipotezy odnosi się do prawdopodobieństwa wykrycia efektu lub różnicy, gdy efekt lub różnica faktycznie występuje. Inaczej mówiąc, jest to prawdopodobieństwo prawidłowego odrzucenia fałszywej hipotezy zerowej.
Oblicza się go w następujący sposób:
Moc = 1 – β
Ogólnie rzecz biorąc, badacze chcą, aby moc testu była wysoka, aby w przypadku wystąpienia efektu lub różnicy test był w stanie go wykryć.
Z powyższego równania widzimy, że najlepszym sposobem na zwiększenie mocy testu jest obniżenie poziomu beta. Najlepszym sposobem na zmniejszenie poziomu beta jest zwykle zwiększenie wielkości próbki.
Poniższe przykłady pokazują, jak obliczyć poziom beta testu hipotezy i dlaczego zwiększenie wielkości próby może obniżyć poziom beta.
Przykład 1: Oblicz Betę dla testu hipotez
Załóżmy, że badacz chce sprawdzić, czy średnia waga gadżetów produkowanych w fabryce jest mniejsza niż 500 uncji. Wiemy, że odchylenie standardowe odważników wynosi 24 uncje i badacz postanawia pobrać losową próbkę 40 widżetów.
Zrealizuje następującą hipotezę przy α = 0,05:
- H0 : µ = 500
- H A : µ < 500
Teraz wyobraź sobie, że średnia waga wyprodukowanych widżetów wynosi w rzeczywistości 490 uncji. Innymi słowy, hipotezę zerową należy odrzucić.
Do obliczenia poziomu beta – prawdopodobieństwa nieodrzucenia hipotezy zerowej, gdy w rzeczywistości powinna zostać odrzucona, możemy zastosować następujące kroki:
Krok 1: Znajdź region bez odrzucenia.
Według kalkulatora krytycznej wartości Z, lewa wartość krytyczna przy α = 0,05 wynosi -1,645 .
Krok 2: Znajdź minimalną próbkę, której nie odrzucimy.
Statystykę testową oblicza się jako z = ( x – μ) / (s/ √n )
Możemy więc rozwiązać to równanie dla średniej próbki:
- x = µ – z*(s/ √n )
- x = 500 – 1,645*(24/ √40 )
- x = 493,758
Krok 3: Określ prawdopodobieństwo, że faktycznie wystąpi minimalna średnia z próbki.
Prawdopodobieństwo to możemy obliczyć w następujący sposób:
- P(Z ≥ (493,758 – 490) / (24/√ 40 ))
- P(Z ≥ 0,99)
Według normalnego kalkulatora CDF prawdopodobieństwo, że Z ≥ 0,99 wynosi 0,1611 .
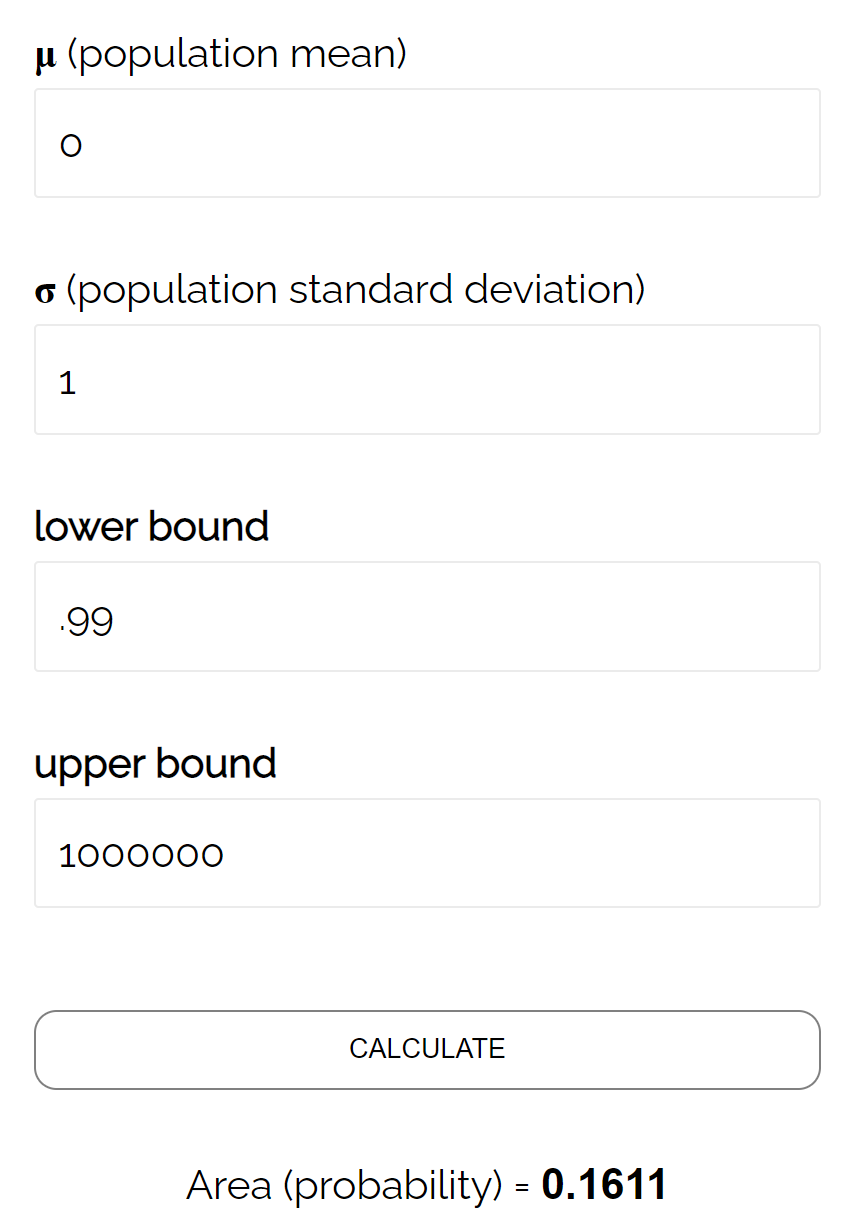
Zatem poziom beta dla tego testu wynosi β = 0,1611. Oznacza to, że istnieje 16,11% szans na niewykrycie różnicy, jeśli rzeczywista średnia wynosi 490 uncji.
Przykład 2: Oblicz Betę dla testu z większą próbką
Załóżmy teraz, że badacz przeprowadza dokładnie ten sam test hipotezy, ale zamiast tego używa próby składającej się z n = 100 widżetów. Możemy powtórzyć te same trzy kroki, aby obliczyć poziom beta dla tego testu:
Krok 1: Znajdź region bez odrzucenia.
Według kalkulatora krytycznej wartości Z, lewa wartość krytyczna przy α = 0,05 wynosi -1,645 .
Krok 2: Znajdź minimalną próbkę, której nie odrzucimy.
Statystykę testową oblicza się jako z = ( x – μ) / (s/ √n )
Możemy więc rozwiązać to równanie dla średniej próbki:
- x = µ – z*(s/ √n )
- x = 500 – 1,645*(24/√ 100 )
- x = 496,05
Krok 3: Określ prawdopodobieństwo, że faktycznie wystąpi minimalna średnia z próbki.
Prawdopodobieństwo to możemy obliczyć w następujący sposób:
- P(Z ≥ (496,05 – 490) / (24/√ 100 ))
- P(Z ≥ 2,52)
Według normalnego kalkulatora CDF prawdopodobieństwo, że Z ≥ 2,52 wynosi 0,0059.
Zatem poziom beta dla tego testu wynosi β = 0,0059. Oznacza to, że istnieje tylko 0,59% szansy na niewykrycie różnicy, jeśli rzeczywista średnia wynosi 490 uncji.
Należy zauważyć, że po prostu zwiększając wielkość próbki z 40 do 100, badaczowi udało się obniżyć poziom beta z 0,1611 do 0,0059.
Bonus: Użyj tego kalkulatora błędów typu II, aby automatycznie obliczyć poziom beta testu.
Dodatkowe zasoby
Wprowadzenie do testowania hipotez
Jak napisać hipotezę zerową (5 przykładów)
Wyjaśnienie wartości P i istotności statystycznej