Czym są reszty w statystyce?

Reszta to różnica między wartością obserwowaną a wartością przewidywaną w analizie regresji .

Oblicza się go w następujący sposób:

Wartość rezydualna = Wartość obserwowana – Wartość przewidywana

Przypomnijmy, że celem regresji liniowej jest ilościowe określenie związku pomiędzy jedną lub większą liczbą zmiennych predykcyjnych a zmienną odpowiedzi . W tym celu regresja liniowa znajduje linię, która najlepiej „pasuje” do danych, zwaną linią regresji najmniejszych kwadratów .

Linia ta generuje prognozę dla każdej obserwacji w zbiorze danych, ale jest mało prawdopodobne, że prognoza dokonana przez linię regresji będzie dokładnie odpowiadać obserwowanej wartości.

Różnica między wartością przewidywaną a obserwowaną stanowi resztę. Jeśli wykreślimy zaobserwowane wartości i nałożymy dopasowaną linię regresji, resztą dla każdej obserwacji będzie pionowa odległość między obserwacją a linią regresji:

Obserwacja ma dodatnią resztę , jeśli jej wartość jest większa niż wartość przewidywana wyznaczona przez linię regresji.

I odwrotnie, obserwacja ma ujemną resztę , jeśli jej wartość jest mniejsza niż wartość przewidywana wyznaczona przez linię regresji.

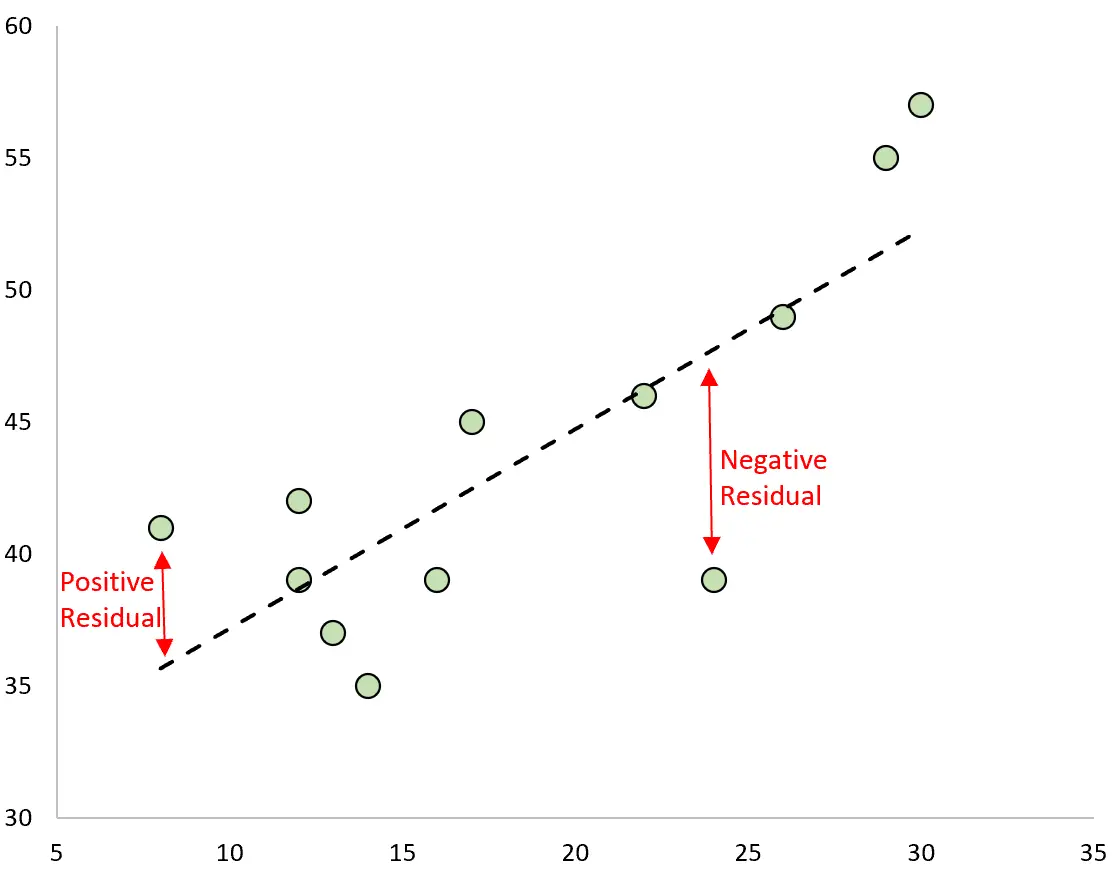
Niektóre obserwacje będą miały reszty dodatnie, inne będą miały reszty ujemne, ale wszystkie reszty będą się sumować do zera .

Przykład obliczenia reszt

Załóżmy, że mamy następujący zbiór danych zawierający łącznie 12 obserwacji:

Jeśli użyjemy oprogramowania statystycznego (takiego jak R , Excel , Python , Stata itp.), aby dopasować linię regresji liniowej do tego zbioru danych, okaże się, że najlepiej dopasowana linia to:

y = 29,63 + 0,7553x

Korzystając z tej linii, możemy obliczyć przewidywaną wartość dla każdej wartości Y w oparciu o wartość X. Na przykład przewidywana wartość pierwszej obserwacji będzie wynosić:

y = 29,63 + 0,7553*(8) = 35,67

Następnie możemy obliczyć resztę tej obserwacji w następujący sposób:

Wartość rezydualna = Wartość obserwowana – Wartość przewidywana = 41 – 35,67 = 5,33

Możemy powtórzyć ten proces, aby znaleźć resztę dla każdej obserwacji:

Jeśli utworzymy wykres rozrzutu w celu wizualizacji obserwacji z dopasowaną linią regresji, zobaczymy, że niektóre obserwacje leżą powyżej linii, a inne poniżej linii:

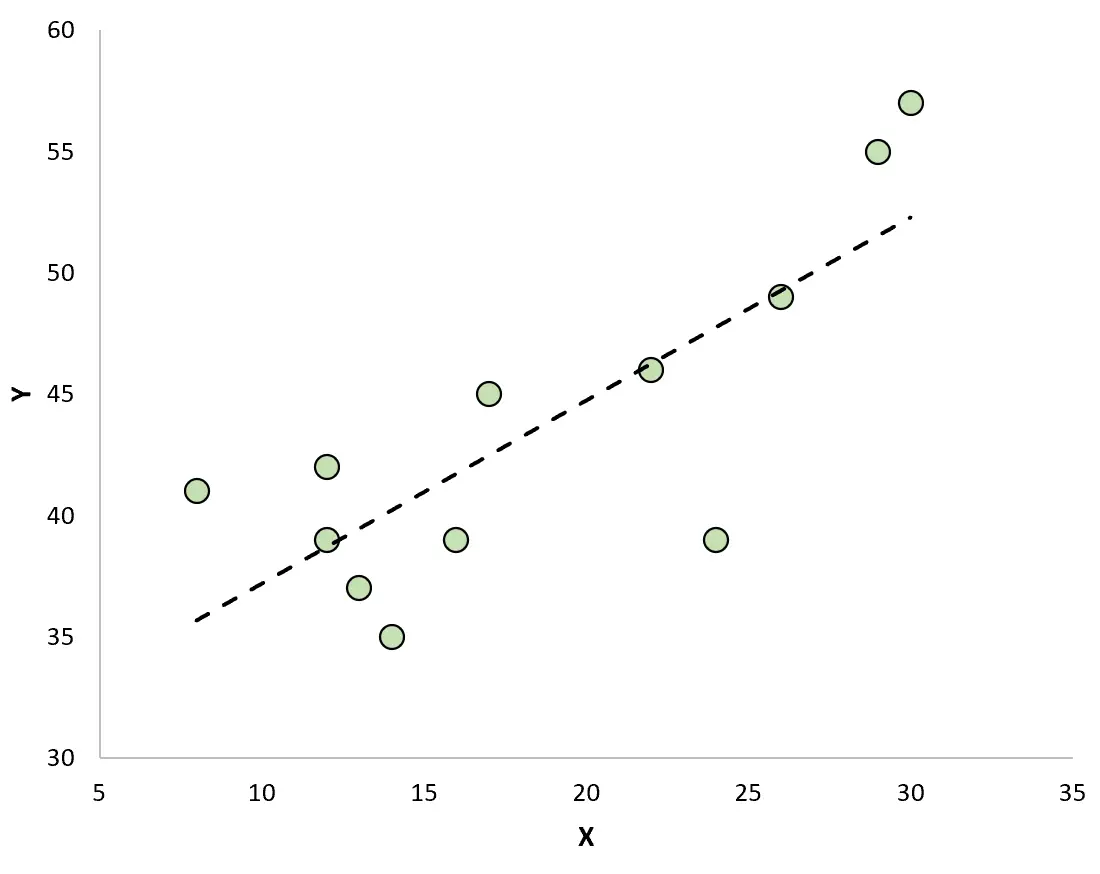
Właściwości pozostałości

Pozostałości mają następujące właściwości:

• Każdej obserwacji w zbiorze danych odpowiada odpowiednia reszta. Zatem jeśli zbiór danych zawiera w sumie 100 obserwacji, model wygeneruje 100 przewidywanych wartości, co daje w sumie 100 reszt.
• Suma wszystkich reszt wynosi zero.
• Średnia wartość reszt wynosi zero.

Jak w praktyce wykorzystuje się pozostałości?

W praktyce reszty są wykorzystywane w regresji z trzech różnych powodów:

1. Ocenić adekwatność modelu.

Po utworzeniu dopasowanej linii regresji możemy obliczyć sumę kwadratów reszt (RSS) , która jest sumą wszystkich kwadratów reszt. Im niższy RSS, tym lepiej model regresji pasuje do danych.

2. Sprawdź założenie normalności.

Jednym z kluczowych założeń regresji liniowej jest to, że reszty mają rozkład normalny.

Aby przetestować tę hipotezę, możemy utworzyć wykres QQ, który jest rodzajem wykresu, którego możemy użyć do określenia, czy reszty modelu mają rozkład normalny.

Jeżeli punkty na wykresie tworzą w przybliżeniu prostą ukośną, wówczas spełnione jest założenie normalności.

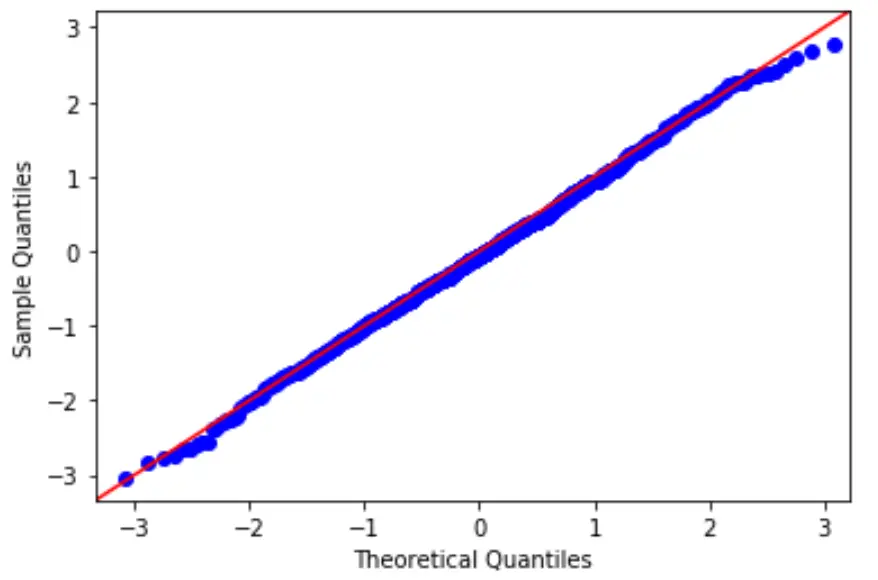
3. Sprawdź założenie o homoskedastyczności.

Innym kluczowym założeniem regresji liniowej jest to, że reszty mają stałą wariancję na każdym poziomie x. Nazywa się to homoskedastycznością. Jeżeli tak nie jest, reszty cierpią na heteroskedastyczność .

Aby sprawdzić, czy to założenie jest spełnione, możemy utworzyć wykres reszt , który jest wykresem rozrzutu przedstawiającym reszty w stosunku do wartości przewidywanych przez model.

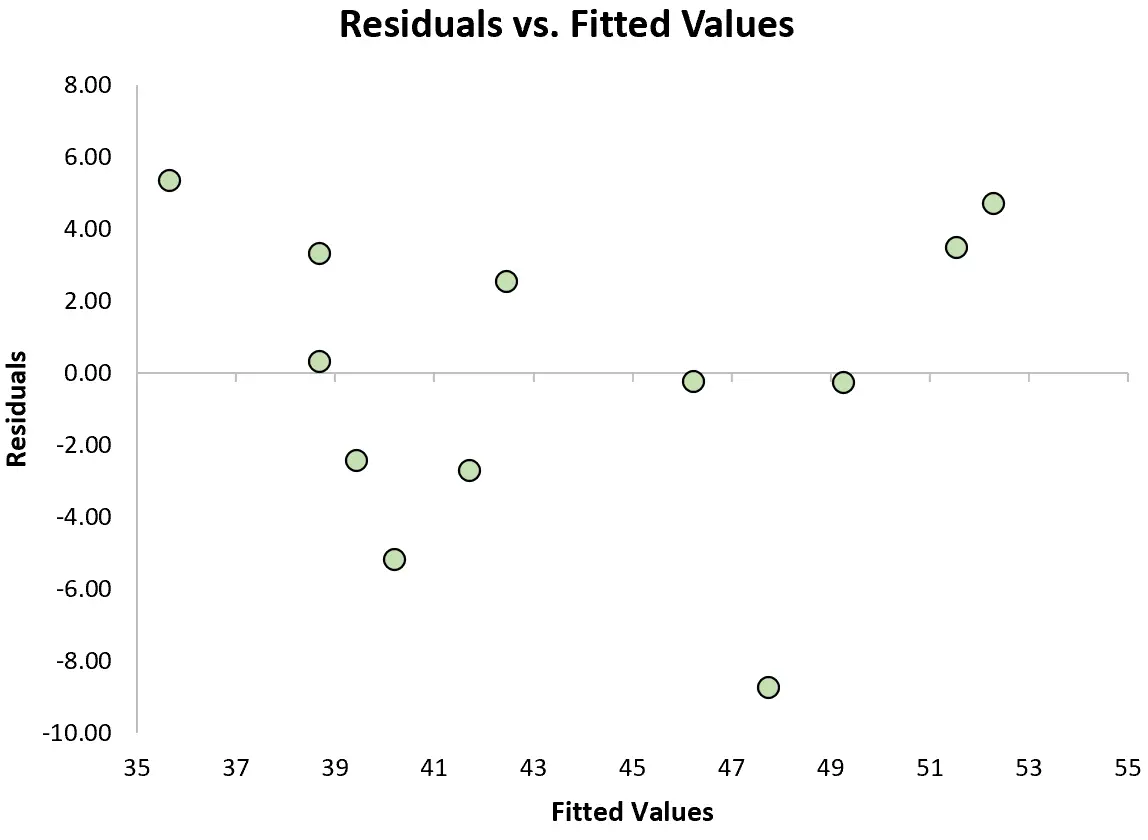
Jeśli reszty na wykresie są w przybliżeniu równomiernie rozłożone wokół zera i nie ma wyraźnego trendu, wówczas ogólnie mówimy, że założenie homoskedastyczności jest spełnione.

Dodatkowe zasoby

Wprowadzenie do prostej regresji liniowej
Wprowadzenie do wielokrotnej regresji liniowej
Cztery założenia regresji liniowej
Jak utworzyć wykres resztowy w programie Excel