Jak analizować reszty w modelu anova

ANOVA („analiza wariancji”) to rodzaj modelu stosowanego do określenia, czy istnieje istotna różnica między średnimi trzech lub więcej niezależnych grup.

dopasowujemy model ANOVA do zbioru danych, zawsze będą pozostałości – reprezentują one różnicę między każdą indywidualną obserwacją a średnią grupową, z której pochodzi obserwacja.

Poniższy przykład pokazuje, jak w praktyce obliczyć reszty dla modelu ANOVA.

Przykład: Obliczanie reszt w ANOVA

Załóżmy, że rekrutujemy 90 osób do udziału w eksperymencie dotyczącym utraty wagi, w ramach którego losowo przydzielamy 30 osób do przestrzegania Programu A, Programu B lub Programu C przez miesiąc.

Możemy wykonać jednoczynnikową analizę ANOVA, aby określić, czy istnieje statystycznie istotna różnica pomiędzy utratą masy ciała wynikającą z trzech programów.

Załóżmy, że obliczymy średnią utratę wagi osób uczestniczących w każdym programie w następujący sposób:

• Program A : 1,58 funta
• Program B : 2,56 funta
• Program C : 4,13 funta

Pozostałości z modelu ANOVA będą różnicą między utratą masy ciała każdej osoby a średnią utratą masy ciała w ramach jej programu.

Na przykład poniższa tabela pokazuje, jak obliczyć reszty dla 10 różnych osób w badaniu:

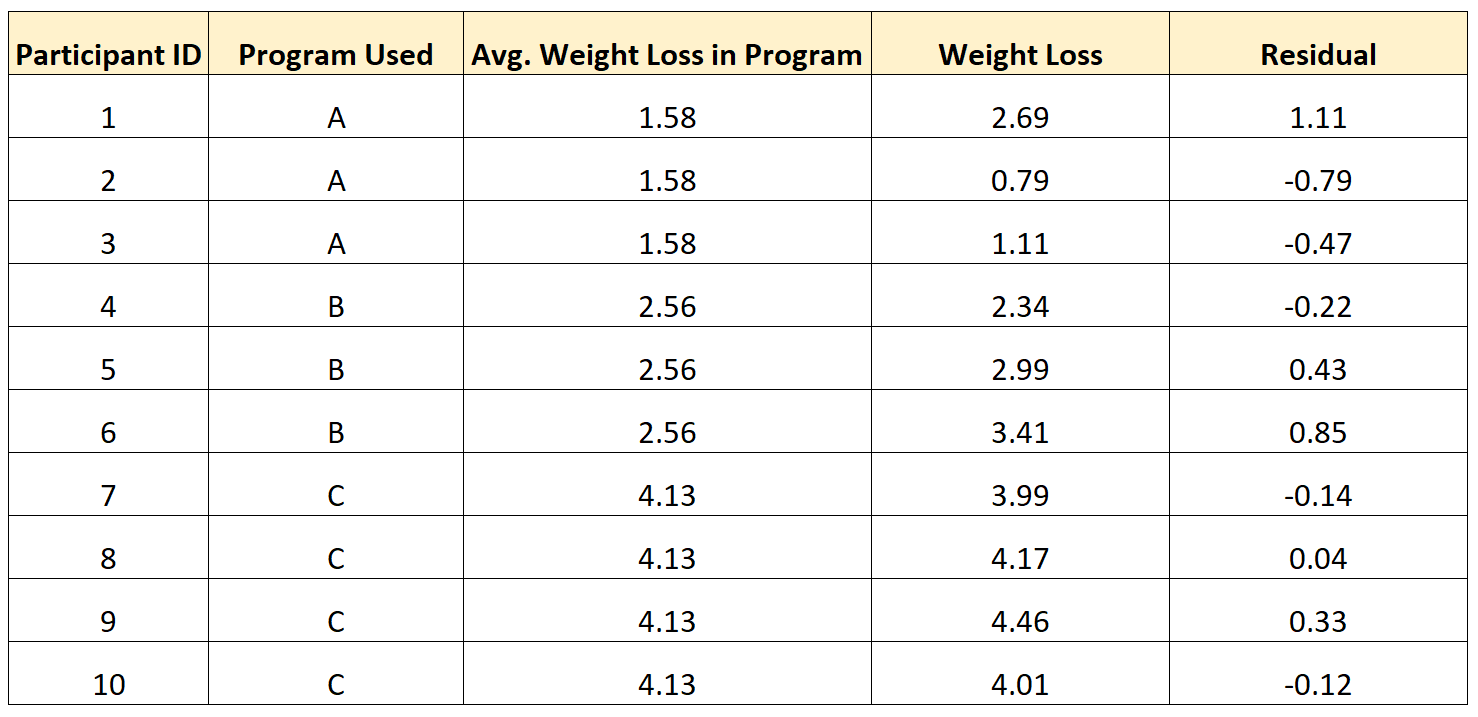
Zwróć uwagę na następujący wzór:

• Osoby, które miały wartość powyżej średniej grupowej, miały dodatnią resztę .
• Osoby, które miały wartość niższą niż średnia w grupie, miały ujemną resztę .

W praktyce obliczalibyśmy reszty dla wszystkich 90 osób.

Jak używać reszt do sprawdzania normalności

Jednym z założeń analizy ANOVA jest to, że reszty mają rozkład normalny.

Najczęstszym sposobem sprawdzenia tego założenia jest utworzenie wykresu QQ .

Jeśli reszty mają rozkład normalny, wówczas punkty na wykresie QQ będą leżeć na prostej ukośnej.

Oto jak wyglądałby wykres QQ w naszym poprzednim przykładzie:

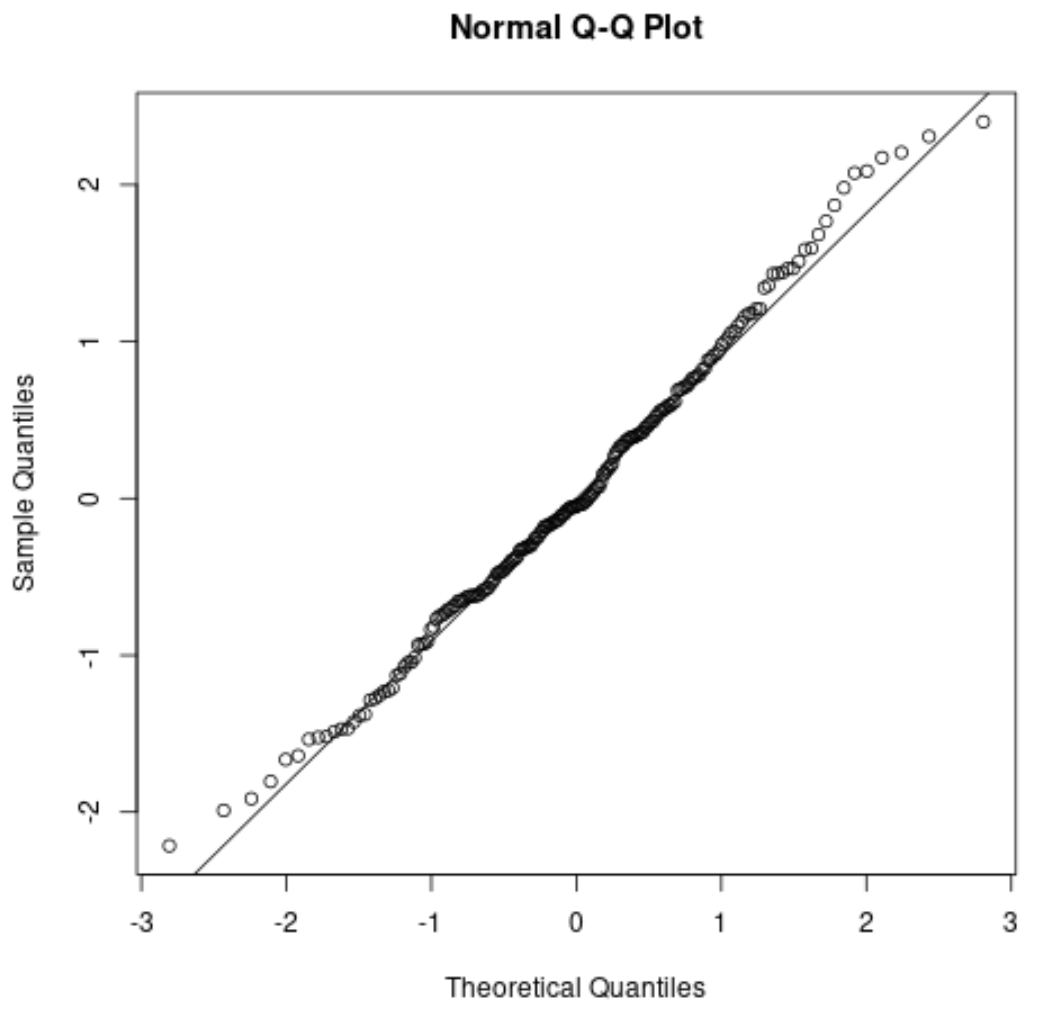
Końcówki odbiegają nieco od prostej linii ukośnej na końcach ogona, ale ogólnie końcówki dobrze przylegają do linii ukośnej. To mówi nam, że założenie normalności jest prawdopodobnie spełnione.

Dla porównania, oto jak mógłby wyglądać wykres QQ dla reszt o rozkładzie normalnym:

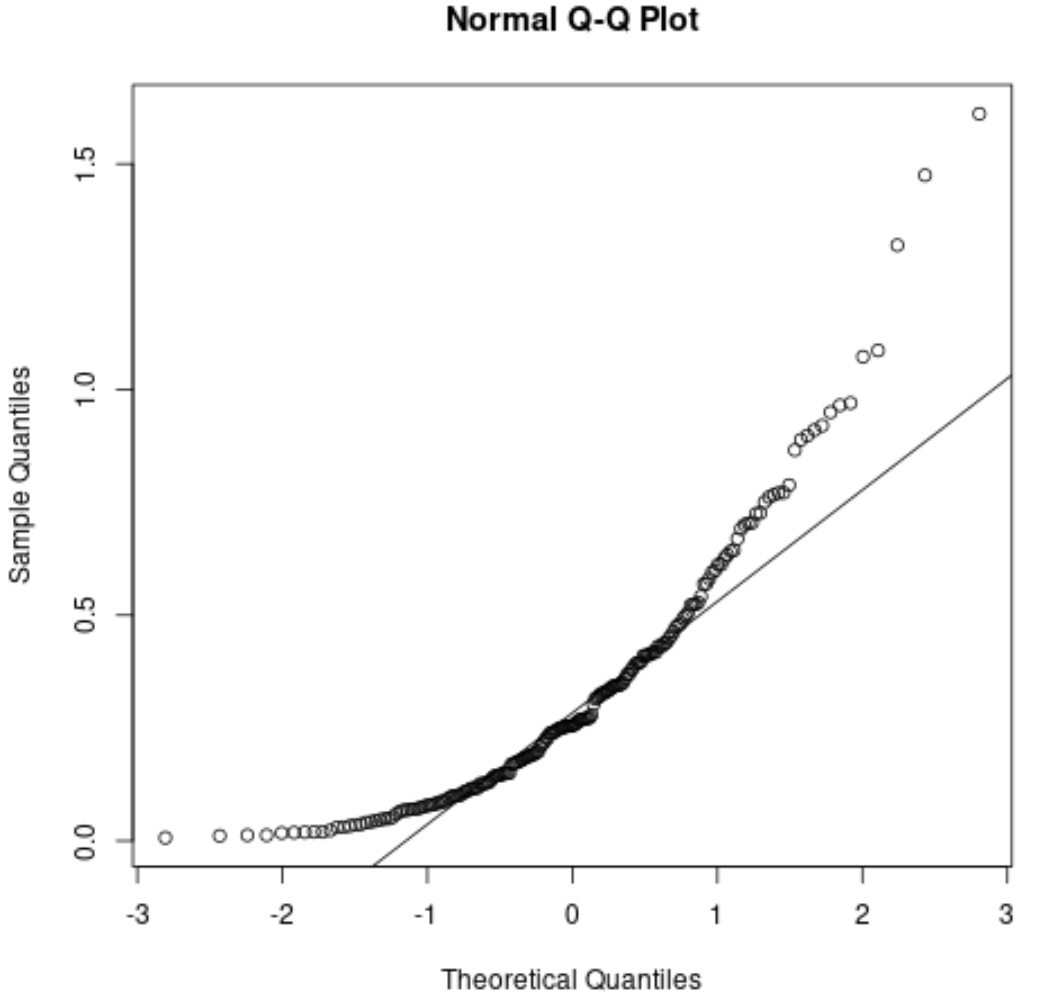
Punkty znacznie odbiegają od prostej linii ukośnej, co wskazuje, że reszty nie mają rozkładu normalnego.

Zapoznaj się z poniższymi samouczkami, aby dowiedzieć się, jak tworzyć wykresy QQ w innym oprogramowaniu:

• Jak utworzyć wykres QQ w programie Excel
• Jak utworzyć wykres QQ w R
• Jak utworzyć wykres QQ w Pythonie

Dodatkowe zasoby

Poniższe artykuły zawierają dodatkowe informacje na temat modeli ANOVA:

Wprowadzenie do jednokierunkowej ANOVA
Jak sprawdzić założenia ANOVA
4 przykłady wykorzystania ANOVA w prawdziwym życiu