Co to są reszty pearsona? (definicja – przykład)
Reszty Pearsona wykorzystuje się w teście niezależności chi-kwadrat w celu analizy różnicy między obserwowaną liczbą komórek a oczekiwaną liczbą komórek w tabeli kontyngencji.
Wzór na obliczenie reszty Pearsona jest następujący:
r ij = (O ij – E ij ) / √ mi ij
Złoto:
- r ij : Reszta Pearsona dla komórki i -tej kolumny i j- tego rzędu
- O ij : Wartość zaobserwowana dla komórki i -tej kolumny i j- tego wiersza
- E ij : Oczekiwana wartość komórki i- tej kolumny i j- tego wiersza
Podobną miarą jest standaryzowana (skorygowana) reszta Pearsona , którą oblicza się w następujący sposób:
r ij = (O ij – E ij ) / √ mi ij (1-n ja+ )(1-n +j )
Złoto:
- r ij : Reszta Pearsona dla komórki i -tej kolumny i j- tego rzędu
- O ij : Wartość zaobserwowana dla komórki i -tej kolumny i j- tego wiersza
- E ij : Oczekiwana wartość komórki i- tej kolumny i j- tego wiersza
- p i+ : Suma wiersza podzielona przez sumę całkowitą
- p + j : Suma kolumny podzielona przez sumę całkowitą
Standaryzowane reszty Pearsona mają rozkład normalny ze średnią 0 i odchyleniem standardowym 1. Każda standaryzowana reszta Pearsona o wartości bezwzględnej powyżej pewnych progów (np. 2 lub 3) wskazuje na brak dopasowania.
Poniższy przykład pokazuje, jak w praktyce obliczyć reszty Pearsona.
Przykład: Obliczanie reszt Pearsona
Załóżmy, że badacze chcą zastosować test niezależności chi-kwadrat, aby ustalić, czy płeć jest powiązana z preferencją partii politycznej.
Decydują się pobrać prostą losową próbę 500 wyborców i zapytać ich o preferencje dotyczące partii politycznych.
Wyniki badania przedstawia poniższa tabela kontyngencji:
| Republikański | Demokrata | Niezależny | Całkowity | |
| Mężczyzna | 120 | 90 | 40 | 250 |
| Kobieta | 110 | 95 | 45 | 250 |
| Całkowity | 230 | 185 | 85 | 500 |
Przed obliczeniem reszt Pearsona musimy najpierw obliczyć oczekiwane zliczenia dla każdej komórki w tabeli kontyngencji. W tym celu możemy skorzystać z następującej formuły:
Oczekiwana wartość = (suma wierszy * suma kolumn) / suma tabeli.
Na przykład oczekiwana wartość dla mężczyzn z Partii Republikańskiej wynosi: (230*250) / 500 = 115 .
Możemy powtórzyć tę formułę, aby uzyskać oczekiwaną wartość dla każdej komórki tabeli:
| Republikański | Demokrata | Niezależny | Całkowity | |
| Mężczyzna | 115 | 92,5 | 42,5 | 250 |
| Kobieta | 115 | 92,5 | 42,5 | 250 |
| Całkowity | 230 | 185 | 85 | 500 |
Następnie możemy obliczyć resztę Pearsona dla każdej komórki w tabeli.
Na przykład resztę Pearsona dla komórki zawierającej republikanów można by obliczyć w następujący sposób:
- r ij = (O ij – E ij ) / √ mi ij
- r ij = (120 – 115) / √ 115
- r ij = 0,466
Możemy powtórzyć tę formułę, aby uzyskać resztę Pearsona dla każdej komórki w tabeli:
| Republikański | Demokrata | Niezależny | |
| Mężczyzna | 0,446 | -0,259 | -0,383 |
| Kobieta | -0,446 | 0,259 | 0,383 |
Następnie możemy obliczyć standaryzowaną resztę Pearsona dla każdej komórki w tabeli.
Na przykład standaryzowaną resztę Pearsona dla komórki zawierającej republikanów można by obliczyć w następujący sposób:
- r ij = (O ij – E ij ) / √ mi ij (1-p ja+ )(1-p +j )
- r ij = (120 – 115) / √ 115(1-250/500)(1-230/500)
- r ij = 0,897
Możemy powtórzyć ten wzór, aby otrzymać standaryzowaną resztę Pearsona dla każdej komórki w tabeli:
| Republikański | Demokrata | Niezależny | |
| Mężczyzna | 0,897 | -0,463 | -0,595 |
| Kobieta | -0,897 | 0,463 | 0,595 |
Widzimy, że żadna ze standaryzowanych reszt Pearsona nie ma wartości bezwzględnej większej niż 3, co wskazuje, że żadna z komórek nie przyczynia się do znaczącego braku dopasowania.
Jeśli użyjemy tego kalkulatora internetowego do wykonania testu niezależności chi-kwadrat, okaże się, że wartość p testu wynosi 0,649198 .
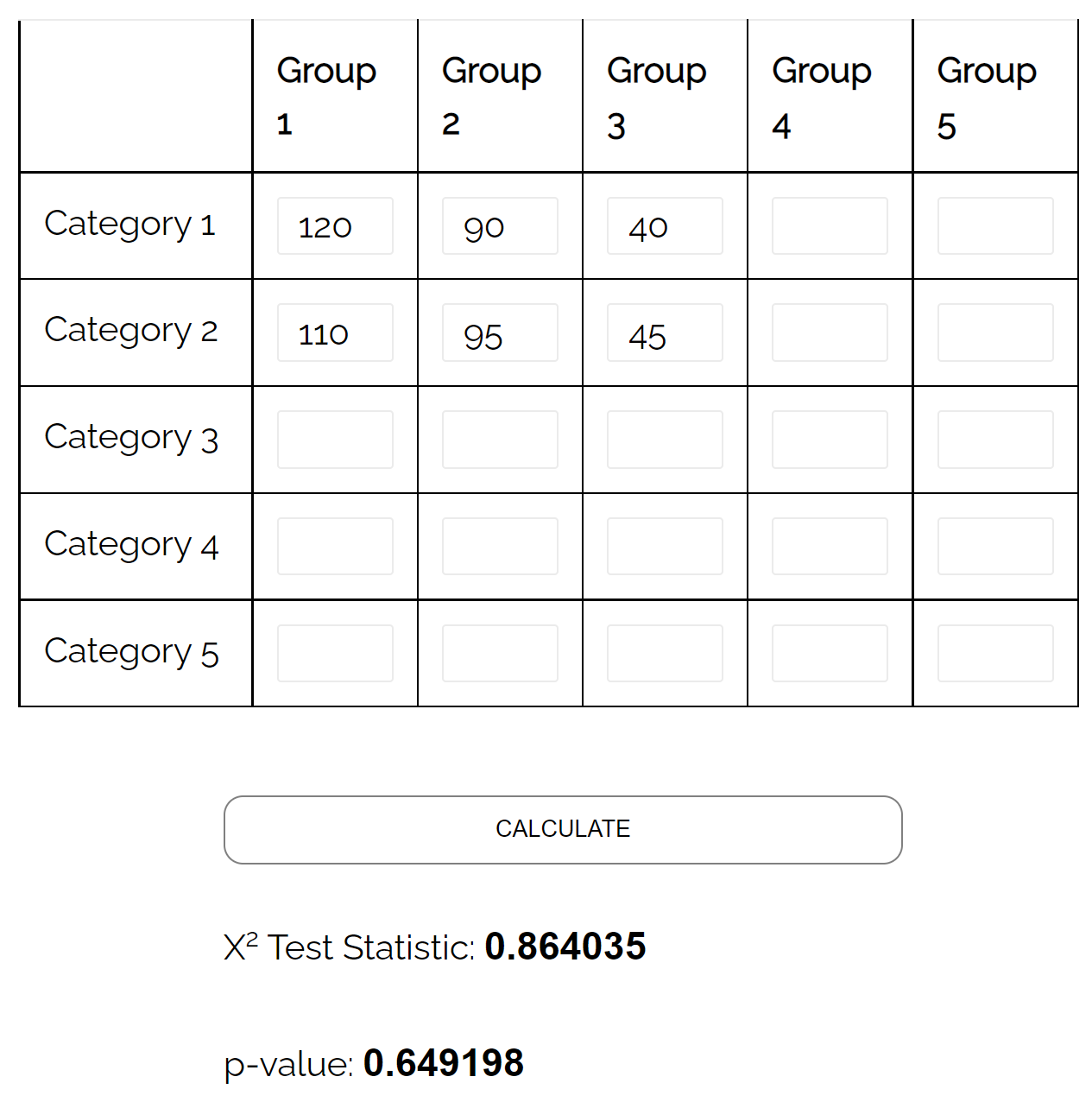
Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie mamy wystarczających dowodów, aby stwierdzić, że istnieje związek między płcią a preferencjami partii politycznych.
Dodatkowe zasoby
Poniższe samouczki wyjaśniają, jak przeprowadzić test niezależności chi-kwadrat przy użyciu różnych programów statystycznych:
Wprowadzenie do testu niezależności chi-kwadrat
Jak wykonać test niezależności chi-kwadrat w programie Excel
Jak wykonać test niezależności chi-kwadrat w R
Test chi-kwadrat kalkulatora niezależności