Prawdopodobieństwo vs. proporcja: jaka jest różnica?

Dwa terminy, które uczniowie często mylą w statystyce, to prawdopodobieństwo i proporcja .

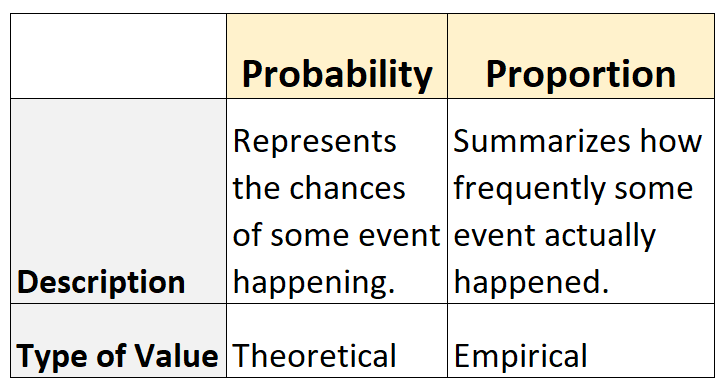
Oto różnica:

• Prawdopodobieństwo oznacza prawdopodobieństwo wystąpienia zdarzenia. To teoretyczne .
• Proporcja podsumowuje, jak często dane zdarzenie faktycznie miało miejsce. To empiryczne .

Często używamy prawdopodobieństwa, gdy mówimy o prawdopodobieństwie wystąpienia zdarzenia w przyszłości.

Natomiast często używamy proporcji, aby opisać, jak często dane wydarzenie faktycznie miało miejsce w przeszłości.

Poniższe przykłady ilustrują różnice między prawdopodobieństwami i proporcjami w różnych scenariuszach.

Przykład 1: Prawdopodobieństwo a proporcja w rzucie monetą

Jeśli rzucimy uczciwą monetą, prawdopodobieństwo , że wypadnie reszka, wynosi 0,5 lub 50% .

Jeśli jednak rzucimy monetą 20 razy, możemy policzyć, ile razy wypadła reszka. Na przykład mógł trafić reszką w 60% przypadków, gdy rzucał.

Prawdopodobieństwo, że moneta wypadnie orłem, jest teoretyczne, ale proporcja przypadków, w których moneta wypadnie reszką, jest empiryczna – w rzeczywistości moglibyśmy policzyć tę proporcję.

Przykład 2: Prawdopodobieństwo a proporcja w rzucie kostkami

Jeśli rzucisz sześciościenną kostką, prawdopodobieństwo , że wypadnie ona na cyfrę „4”, wynosi 1/6, czyli około 16,67% .

Jeśli jednak rzucimy kostką 10 razy, możemy policzyć, ile razy wypadła ona na 4. Na przykład, może wypadła na „4” w 20% rzutów.

Prawdopodobieństwo wyrzucenia „4” jest teoretyczne, ale odsetek przypadków, w których kość wylądowała na „4” jest empiryczny – w rzeczywistości moglibyśmy policzyć tę proporcję.

Przykład 3: Prawdopodobieństwo a prawdopodobieństwo Proporcja w Spinnerach

Jeśli zakręcimy ruletką podzieloną na cztery równe części – czerwoną, niebieską, zieloną i fioletową – prawdopodobieństwo , że w danym obrocie wyląduje na fioletowo, wynosi 25% .

Jeśli jednak zakręcimy kołem ruletki 100 razy, możemy policzyć, ile razy ruletka wypadła na fioletowo. Na przykład może trafił na fiolet w 15% obrotów.

Prawdopodobieństwo, że ruletka wyląduje na fioletowo, jest teoretyczne, ale odsetek przypadków, w których ruletka wyląduje na fioletowo, jest empiryczny – w rzeczywistości możemy policzyć tę proporcję.

Przykład 4: Prawdopodobieństwo a proporcja w grach karcianych

W standardowej talii 52 kart znajdują się 4 królowe. Zatem prawdopodobieństwo wybrania hetmana w losowaniu wynosi 4/52 = 7,69% .

Jeśli jednak losowo dobierzemy (i zastąpimy dobraną kartę) 50 razy, w rzeczywistości możemy policzyć, ile razy losujemy hetman. Na przykład, może wylosujemy damę w 10% losowań.

Prawdopodobieństwo wybrania królowej jest teoretyczne, ale odsetek przypadków, w których rzeczywiście wybieramy królową, jest empiryczny – w rzeczywistości moglibyśmy policzyć tę proporcję.

Dodatkowe zasoby

Prawdopodobieństwo a prawdopodobieństwo: jaka jest różnica?
Prawo prawdopodobieństwa całkowitego: definicja i przykłady