Prawdopodobieństwo empiryczne

W tym artykule wyjaśniamy, jak obliczyć prawdopodobieństwo empiryczne. Dowiesz się, czym jest prawdopodobieństwo empiryczne, jaki jest jego wzór, przykład i jakie są różnice między prawdopodobieństwem empirycznym a prawdopodobieństwem teoretycznym.

Co to jest prawdopodobieństwo empiryczne?

Prawdopodobieństwo empiryczne to miara statystyczna oparta na eksperymentach empirycznych lub faktach, która wskazuje prawdopodobieństwo wystąpienia zdarzenia.

Innymi słowy, prawdopodobieństwo empiryczne jest obliczane na podstawie wyników eksperymentu i mówi nam, jak prawdopodobne jest wystąpienie zdarzenia.

Im częściej eksperyment będzie powtarzany, tym dokładniejsze będzie uzyskane prawdopodobieństwo empiryczne. Dlatego też tego typu prawdopodobieństwo wyznacza się najczęściej za pomocą programów komputerowych, które symulują tysiące iteracji i są w stanie je przeanalizować w bardzo krótkim czasie.

Prawdopodobieństwo empiryczne to liczba z zakresu od 0 do 1. Im większe prawdopodobieństwo wystąpienia zdarzenia, tym większe prawdopodobieństwo empiryczne i odwrotnie, im mniejsze prawdopodobieństwo wystąpienia zdarzenia, tym mniejsze jest jego prawdopodobieństwo empiryczne.

Empiryczny wzór na prawdopodobieństwo

Wzór na prawdopodobieństwo empiryczne to liczba przypadków wystąpienia zdarzenia podczas eksperymentu podzielona przez całkowitą liczbę powtórzeń eksperymentu.

Na przykład, jeśli spojrzymy na drzewo dziesięć razy i siedem razy widzieliśmy ptaka na drzewie, empiryczne prawdopodobieństwo zobaczenia ptaka podczas patrzenia na drzewo będzie wynosić:

Przykład prawdopodobieństwa empirycznego

Rozważając definicję prawdopodobieństwa empirycznego, rozwiążemy krok po kroku ćwiczenie dotyczące tego typu prawdopodobieństwa. W ten sposób można zobaczyć, jak obliczane jest prawdopodobieństwo empiryczne.

• Oblicza empiryczne prawdopodobieństwo zdarzeń elementarnych składających się na losowy eksperyment polegający na rzucie kostką.

Najpierw obliczymy teoretyczne prawdopodobieństwo porównania uzyskanych wyników eksperymentalnych z wynikami teoretycznymi. Przy rzucie kostką istnieje sześć możliwych wyników (1, 2, 3, 4, 5 i 6), zatem teoretyczne prawdopodobieństwo każdego elementarnego zdarzenia wynosi:

Aby rozwiązać to ćwiczenie, musimy kilka razy symulować rzut kostką i zapisywać wyniki w tabeli kontyngencji. Możemy do tego posłużyć się na przykład programem Excel.

Abyś mógł zobaczyć, jak ważne jest liczba przeprowadzonych eksperymentów, najpierw przeprowadzimy symulację dziesięciu startów, potem stu, a na koniec tysiąca. Zatem wyniki uzyskane z symulacji pierwszych 10 losowych rzutów kostką są następujące:

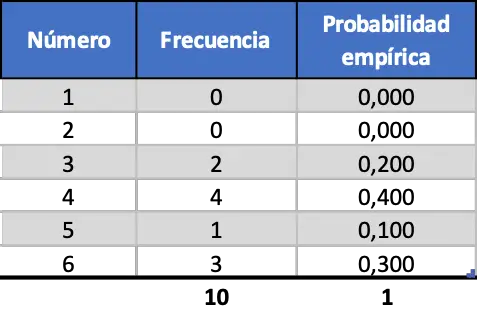
Jak widać, prawdopodobieństwa empiryczne uzyskane poprzez symulację tylko dziesięciu rzutów nie są zbliżone do prawdopodobieństw teoretycznych (0,167).

Jednak w miarę zwiększania liczby eksperymentów te dwa wskaźniki stają się coraz bardziej podobne. Spójrz na symulację 100 uruchomień:

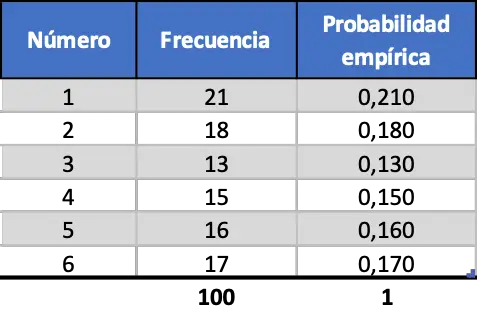
Teraz prawdopodobieństwo empiryczne obliczone dla każdej liczby na kostce jest bardziej zbliżone do prawdopodobieństwa teoretycznego, jednak nadal otrzymujemy bardzo różne wartości.

Na koniec wykonujemy tę samą procedurę, ale symulujemy 1000 uruchomień:

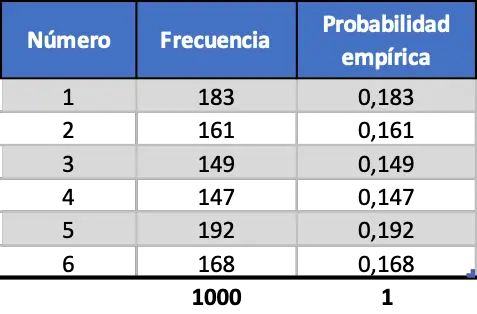
Jak widać w ostatniej tabeli kontyngencji, teraz wartości prawdopodobieństw empirycznych są bardzo zbliżone do prawdopodobieństw teoretycznych.

Reasumując, im bardziej zwiększymy liczbę przeprowadzanych eksperymentów, tym wartość prawdopodobieństwa empirycznego zdarzenia będzie bliższa jego prawdopodobieństwu teoretycznemu . Regułę tę definiuje się jako prawo wielkich liczb , które stwierdza, że im więcej danych, tym wartości eksperymentalne będą bliższe wartościom teoretycznym.

Co więcej, jeśli porównamy trzy tabele częstości, zobaczymy, że prawdopodobieństwo empiryczne nie jest ostateczne, ale zmienia się w zależności od liczby przeprowadzonych eksperymentów. Oznacza to, że trzeba wiedzieć, jak interpretować uzyskane wartości.

Prawdopodobieństwo empiryczne i prawdopodobieństwo teoretyczne

Na koniec przeanalizujemy pojęcie prawdopodobieństwa empirycznego i prawdopodobieństwa teoretycznego, ponieważ choć są to dwa rodzaje prawdopodobieństw, mają zupełnie inne znaczenie.

Różnica między prawdopodobieństwem empirycznym a prawdopodobieństwem teoretycznym (lub prawdopodobieństwem klasycznym) polega na tym, że prawdopodobieństwo empiryczne oblicza się na podstawie danych zebranych z prawdziwego doświadczenia, natomiast prawdopodobieństwo teoretyczne oblicza się z uwzględnieniem idealnych warunków, bez przeprowadzania żadnego eksperymentu.

Oznacza to, że aby znaleźć prawdopodobieństwo empiryczne, należy przeprowadzić symulację eksperymentu i przeprowadzić obliczenia na podstawie uzyskanych wyników. Aby jednak poznać prawdopodobieństwo teoretyczne, nie trzeba przeprowadzać żadnego eksperymentu, lecz raczej teoretyczne obliczenia.

Dodatkowo poziom błędu systematycznego definiuje się jako różnicę między prawdopodobieństwem empirycznym a prawdopodobieństwem teoretycznym. Odchylenie może być dodatnie lub ujemne, ale bardzo trudno jest wynieść zero, ponieważ oznaczałoby to, że losowy eksperyment osiąga jedynie teoretyczne prawdopodobieństwo, co jest bardzo mało prawdopodobne.