Prawdopodobieństwo późniejsze: definicja + przykład

Prawdopodobieństwo a posteriori to zaktualizowane prawdopodobieństwo, że zdarzenie nastąpi po uwzględnieniu nowych informacji.

Na przykład może nas interesować prawdopodobieństwo wystąpienia zdarzenia „A” po uwzględnieniu zdarzenia „B”, które właśnie nastąpiło. Prawdopodobieństwo późniejsze możemy obliczyć za pomocą następującego wzoru:

P(A|B) = P(A) * P(B|A) / P(B)

Złoto:

P(A|B) = prawdopodobieństwo zajścia zdarzenia A, przy założeniu, że zaszło zdarzenie B. Zauważ, że „| » oznacza „dany”.

P(A) = prawdopodobieństwo wystąpienia zdarzenia A.

P(B) = prawdopodobieństwo wystąpienia zdarzenia B.

P(B|A) = prawdopodobieństwo wystąpienia zdarzenia B, przy założeniu, że zaszło zdarzenie A.

Przykład: Obliczanie prawdopodobieństwa późniejszego

Las składa się z 20% dębów i 80% klonów. Załóżmy, że wiemy, że 90% dębów jest zdrowych, a tylko 50% klonów jest zdrowych. Załóżmy, że z daleka można stwierdzić, że dane drzewo jest zdrowe. Jakie jest prawdopodobieństwo, że jest to dąb?

Przypomnijmy, że prawdopodobieństwo zajścia zdarzenia A, jeśli zaszło zdarzenie B, wynosi:

P(A|B) = P(A) * P(B|A) / P(B)

W tym przykładzie prawdopodobieństwo, że jest to dąb, przy założeniu, że jest zdrowe, wynosi:

P(Dąb|Zdrowy) = P(Dąb) * P(Zdrowy|Dąb) / P(Zdrowy)

P(Dąb) = Prawdopodobieństwo, że dane drzewo jest dębem wynosi 0,2, ponieważ 20% wszystkich drzew w lesie to dęby.

P(Zdrowe) = Prawdopodobieństwo, że dane drzewo jest zdrowe, można obliczyć w następujący sposób: (0,20)*(0,9) + (0,8)*(0,5) = 0,58 .

P(Zdrowy|Dąb) = Prawdopodobieństwo, że drzewo jest zdrowe, biorąc pod uwagę, że jest to dąb, wynosi 0,9 , ponieważ powiedziano nam, że 90% dębów jest zdrowych.

Korzystając z tych trzech liczb, możemy obliczyć prawdopodobieństwo, że drzewo jest dębem, pod warunkiem, że jest zdrowe:

P(Dąb|Zdrowy) = P(Dąb) * P(Zdrowy|Dąb) / P(Zdrowy) = (0,2) * (0,9) / (0,58) = 0,3103 .

Aby intuicyjnie zrozumieć to prawdopodobieństwo, załóżmy, że poniższa siatka przedstawia ten las złożony ze 100 drzew. Dokładnie 20 drzew to dęby, a 18 z nich jest zdrowych. Pozostałe 80 drzew to klony, a 40 z nich jest zdrowych.

(O = dąb, M = klon, zielony = zdrowy, czerwony = niezdrowy)

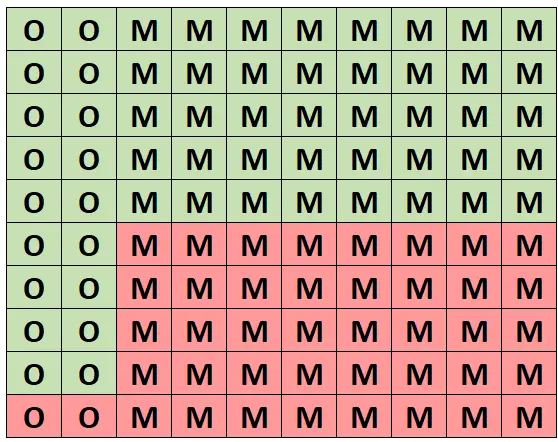
Spośród wszystkich drzew dokładnie 58 jest zdrowych, z czego 18 to dęby. Jeśli więc wiemy, że wybraliśmy zdrowe drzewo, prawdopodobieństwo, że jest to dąb wynosi 18/58 = 0,3103 .

Kiedy należy stosować prawdopodobieństwo późniejsze?

Prawdopodobieństwo późniejsze jest wykorzystywane w wielu różnych dziedzinach, w tym w finansach, medycynie, ekonomii i prognozowaniu pogody.

Celem wykorzystania prawdopodobieństw późniejszych jest aktualizacja wcześniejszego przekonania, jakie mieliśmy na jakiś temat, gdy tylko uzyskamy nowe informacje.

Przypomnijmy z poprzedniego przykładu, że wiedzieliśmy, że prawdopodobieństwo, że dane drzewo w lesie to dąb wynosi 20%. Nazywa się to prawdopodobieństwem a priori . Gdybyśmy po prostu wybrali losowo drzewo, wiedzieliśmy, że prawdopodobieństwo, że jest to dąb, wynosiło 0,20.

Jednak gdy otrzymaliśmy nowe informacje, że wybrane przez nas drzewo jest zdrowe, mogliśmy wykorzystać te nowe informacje do ustalenia, że prawdopodobieństwo późniejsze tego, że to drzewo jest dębem, wynosi zamiast tego 0,3103.

W prawdziwym świecie ludzie nieustannie odkrywają nowe informacje. Te nowe informacje pomagają nam zaktualizować nasze dotychczasowe przekonania. W ujęciu statystycznym oznacza to, że jesteśmy w stanie wygenerować prawdopodobieństwa późniejsze zaistniałych zdarzeń, co pomaga nam uzyskać dokładniejsze zrozumienie świata i pozwala na dokładniejsze przewidywanie przyszłych wydarzeń.