Prawdopodobieństwo przecięcia się zdarzeń
W tym artykule wyjaśniono, jak obliczyć prawdopodobieństwo przecięcia się zdarzeń. Dowiesz się więc, jaki jest wzór na prawdopodobieństwo przecięcia się zdarzeń, a ponadto dowiesz się ćwiczeń rozwiązywanych krok po kroku.
Jakie jest skrzyżowanie wydarzeń?
W teorii prawdopodobieństwa przecięcie zdarzeń jest operacją zdarzeń, której wynik składa się ze zdarzeń elementarnych wspólnych dla wszystkich zdarzeń operacji. Oznacza to, że przecięcie zdarzeń A i B tworzą wszystkie zdarzenia należące jednocześnie do A i B.
Przecięcie dwóch zdarzeń jest oznaczone symbolem ⋂. Zatem przecięcie zdarzeń A i B zapisuje się jako A⋂B.
Na przykład w losowym eksperymencie polegającym na rzucie kostką, jeśli jednym zdarzeniem jest wyrzucenie liczby parzystej A={2, 4, 6}, a innym zdarzeniem wyrzucenie liczby większej niż trzy B={4, 5, 6 }, przecięcie dwóch zdarzeń to A⋂B={4, 6}.
Wzór na prawdopodobieństwo przecięcia się zdarzeń
Prawdopodobieństwo przecięcia się dwóch zdarzeń jest równe prawdopodobieństwu wystąpienia jednego zdarzenia pomnożonemu przez prawdopodobieństwo warunkowe wystąpienia drugiego zdarzenia, przy uwzględnieniu pierwszego zdarzenia.
Zatem wzór na prawdopodobieństwo przecięcia dwóch zdarzeń to P(A⋂B)=P(A) P(B|A)=P(B) P(A|B).
![]()
Złoto:
-

I

Są to dwa zdarzenia zależne.
-

jest prawdopodobieństwem przecięcia zdarzenia A i zdarzenia B.
-

jest prawdopodobieństwem wystąpienia zdarzenia A.
-

jest prawdopodobieństwem warunkowym wystąpienia zdarzenia B przy danym zdarzeniu A.
-

jest prawdopodobieństwem wystąpienia zdarzenia B.
-
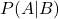
jest prawdopodobieństwem warunkowym wystąpienia zdarzenia A przy danym zdarzeniu B.
Jeżeli jednak te dwa zdarzenia są niezależne, oznacza to, że prawdopodobieństwo wystąpienia jednego zdarzenia nie zależy od tego, czy zajdzie drugie zdarzenie. Zatem wzór na prawdopodobieństwo przecięcia dwóch niezależnych zdarzeń jest następujący:
![]()
Złoto:
-

I

To dwa niezależne zdarzenia.
-

jest prawdopodobieństwem przecięcia zdarzenia A i zdarzenia B.
-

jest prawdopodobieństwem wystąpienia zdarzenia A.
-

jest prawdopodobieństwem wystąpienia zdarzenia B.
Rzeczywiste przykłady prawdopodobieństwa przecięcia zdarzeń
Następnie zostawiamy dwa przykłady rozwiązane krok po kroku, abyś mógł zobaczyć, jak obliczane jest prawdopodobieństwo przecięcia dwóch zdarzeń. Najpierw zobaczymy przykład przecięcia dwóch niezależnych zdarzeń, a następnie dwóch zdarzeń zależnych, dzięki czemu będziesz mógł zobaczyć oba przypadki.
Prawdopodobieństwo przecięcia dwóch niezależnych zdarzeń
- Losowanie rozpoczyna się trzy razy z rzędu. Znajdź prawdopodobieństwo wyrzucenia orła we wszystkich trzech rzutach.
W tym przypadku zdarzenia, dla których chcemy obliczyć łączne prawdopodobieństwo, są niezależne, ponieważ wynik losowania nie zależy od wyniku uzyskanego w poprzednim losowaniu. Dlatego, aby określić prawdopodobieństwo wyrzucenia trzech kolejnych orłów, musimy skorzystać ze wzoru na prawdopodobieństwo przecięcia dla niezależnych zdarzeń:
![]()
Podczas losowania możliwe są tylko dwa wyniki, możemy otrzymać orzeł lub reszkę. Zatem prawdopodobieństwo wyrzucenia orła lub reszki podczas rzucania monetą wynosi:
![]()
Aby więc obliczyć prawdopodobieństwo wyrzucenia orła we wszystkich trzech rzutach monetą, musimy pomnożyć prawdopodobieństwo wyrzucenia orła przez trzy:
![Rendered by QuickLaTeX.com \begin{aligned}P(\text{cara}\cap \text{cara}\cap \text{cara})&=P(\text{cara})\cdot P(\text{cara})\cdot P(\text{cara})\\[2ex]&=0,5\cdot 0,5\cdot 0,5\\[2ex]&=0,125\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-54abe4c41545eb6e46fd1cf97f8a3253_l3.png)
Krótko mówiąc, prawdopodobieństwo wyrzucenia orła trzy razy z rzędu wynosi 12,5%.
Prawdopodobieństwo przecięcia dwóch zależnych zdarzeń
- W pustym pudełku wkładamy 8 kul niebieskich, 4 pomarańczowe i 2 zielone. Jeśli najpierw losujemy jedną, potem drugą kulę, nie wkładając pierwszej wylosowanej do pudełka, jakie jest prawdopodobieństwo, że pierwsza kula będzie niebieska, a druga pomarańczowa?
W tym przypadku zdarzenia są zależne, ponieważ prawdopodobieństwo podniesienia kulki pomarańczowej w drugim losowaniu zależy od koloru kulki wylosowanej w pierwszym losowaniu. Dlatego, aby obliczyć prawdopodobieństwo, o które pyta nas problem, musimy skorzystać ze wzoru na prawdopodobieństwo przecięcia zdarzeń zależnych:
![]()
Prawdopodobieństwo otrzymania niebieskiej kuli w pierwszym losowaniu jest łatwe do ustalenia, wystarczy podzielić liczbę niebieskich kul przez całkowitą liczbę kul:
![]()
Z drugiej strony prawdopodobieństwo wylosowania kulki pomarańczowej po wzięciu kulki niebieskiej jest obliczane inaczej, ponieważ liczba kul pomarańczowych jest inna, a dodatkowo w pudełku jest teraz o jedną kulę mniej:
![]()
Zatem prawdopodobieństwo wylosowania najpierw niebieskiej, a następnie pomarańczowej kuli oblicza się, mnożąc oba prawdopodobieństwa podane powyżej:
![Rendered by QuickLaTeX.com \begin{array}{l}P(\text{bola azul}\cap\text{bola naranja})=\\[2ex]=P(\text{bola azul})\cdot P(\text{bola naranja}|\text{bola azul})=\\[2ex]=0,57\cdot 0,31= \\[2ex]=0,18\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-94896f8575aeb7e73cc056595920fedb_l3.png)
Właściwości skrzyżowania zdarzeń
W teorii prawdopodobieństwa przecięcie zdarzeń ma następujące właściwości:
- Właściwość przemienna: Kolejność zdarzeń przecięcia nie zmienia wyniku operacji.
![]()
- Właściwość asocjacji: Przecięcie trzech zdarzeń można obliczyć w dowolnej kolejności, ponieważ wynik jest taki sam.
![]()
- Własność rozdzielcza: przecięcie zdarzeń spełnia własność rozdzielczą w połączeniu zdarzeń.
![]()