Prawdopodobieństwo warunkowe (lub prawdopodobieństwo warunkowe)

Tutaj dowiesz się, czym jest prawdopodobieństwo warunkowe (lub prawdopodobieństwo warunkowe). Wyjaśniamy, jak obliczane jest prawdopodobieństwo warunkowe, na przykładzie i właściwościach tego rodzaju prawdopodobieństwa. Ponadto będziesz mógł ćwiczyć krok po kroku rozwiązywane ćwiczenia z prawdopodobieństwa warunkowego.

Co to jest prawdopodobieństwo warunkowe?

Prawdopodobieństwo warunkowe , zwane także prawdopodobieństwem warunkowym , jest miarą statystyczną wskazującą prawdopodobieństwo, że zdarzenie A nastąpi, jeśli wystąpi inne zdarzenie B. Oznacza to, że prawdopodobieństwo warunkowe P(A|B) odnosi się do prawdopodobieństwa wystąpienia zdarzenia A po wystąpieniu zdarzenia B.

Prawdopodobieństwo warunkowe zapisywane jest pionową kreską pomiędzy dwoma zdarzeniami: P(A|B) i brzmi: „prawdopodobieństwo warunkowe zdarzenia A przy danym zdarzeniu B”.

Należy pamiętać, że wartość prawdopodobieństwa warunkowego to liczba z zakresu od 0 do 1. Im wyższe prawdopodobieństwo warunkowe, tym większe prawdopodobieństwo, że zdarzenie A nastąpi, gdy nastąpi zdarzenie B, ale im niższe prawdopodobieństwo warunkowe, tym mniejsze prawdopodobieństwo, że zdarzenie A nastąpi, gdy nastąpi zdarzenie B.

Wzór na prawdopodobieństwo warunkowe

Prawdopodobieństwo warunkowe zdarzenia A dla danego zdarzenia B jest równe prawdopodobieństwu przecięcia zdarzenia A i zdarzenia B podzielonemu przez prawdopodobieństwo zdarzenia B.

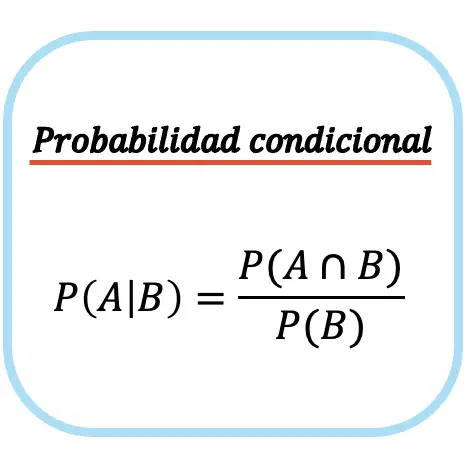
Należy pamiętać, że wzór na prawdopodobieństwo warunkowe (lub prawdopodobieństwo warunkowe) można zastosować tylko wtedy, gdy prawdopodobieństwo wystąpienia zdarzenia bezwarunkowego jest niezerowe, tj. P(B)≠0. Inaczej mówiąc, jeśli możliwe jest wystąpienie zdarzenia B.

Prawdopodobieństwo warunkowe można również obliczyć z jego odwrotności, tzn. jeśli znane jest P(B|A), można wyznaczyć P(A|B). Ale aby to zrobić, musisz zastosować twierdzenie Bayesa, możesz zobaczyć, z czego to twierdzenie się składa tutaj:

Przykład prawdopodobieństwa warunkowego

Kiedy już poznamy definicję i wzór prawdopodobieństwa warunkowego, krok po kroku rozwiążemy przykład tego typu prawdopodobieństwa, aby w pełni zrozumieć jego znaczenie.

• Po zdaniu egzaminu w klasie liczącej 30 uczniów zebrano dane, aby dowiedzieć się, ilu uczniów się uczyło, a ilu zdało egzamin. Wyniki przedstawiono w poniższej tabeli awaryjnej. Na podstawie zebranych danych oblicz warunkowe prawdopodobieństwo zdania egzaminu, jeśli już się uczyłeś.

Aby uzyskać prawdopodobieństwo warunkowe, musimy zastosować wzór, który widzieliśmy wcześniej:

Dlatego najpierw musimy znaleźć prawdopodobieństwo, że student studiował, studiował i zdał egzamin. Aby obliczyć prawdopodobieństwo, że student się uczył, wystarczy skorzystać z reguły Laplace’a, to znaczy podzielić liczbę studentów, którzy studiowali, przez całkowitą liczbę obserwacji:

Prawdopodobieństwo, że student studiował i zdał egzamin w tym samym czasie, możemy znaleźć z tabeli kontyngencji, dzieląc liczbę studentów, którzy studiowali i zaliczyli przez sumę:

Zatem prawdopodobieństwo, że student zda egzamin, jeśli się uczył, wynosi:

Prawdopodobieństwo warunkowe zdarzeń zależnych i niezależnych

W tej sekcji zobaczymy, jaki jest związek między prawdopodobieństwem warunkowym a zdarzeniami zależnymi i niezależnymi (lub zdarzeniami zależnymi i niezależnymi). Ponieważ chociaż są to różne pojęcia, te dwa typy zdarzeń są powiązane z prawdopodobieństwem warunkowym.

Dwa zdarzenia (lub wystąpienia) są niezależne, gdy prawdopodobieństwo ich wystąpienia nie zależy od siebie. W takim przypadku punkt przecięcia obu zdarzeń jest równy iloczynowi prawdopodobieństwa każdego zdarzenia z osobna. Dlatego wzór na prawdopodobieństwo warunkowe jest uproszczony:

Krótko mówiąc, jeśli zdarzenia A i B są niezależne, prawdopodobieństwo warunkowe zdarzenia A przy danym zdarzeniu B jest dokładnie równe prawdopodobieństwu wystąpienia zdarzenia A.

Z drugiej strony, gdy dwa zdarzenia są zależne, oznacza to, że prawdopodobieństwo jednego zdarzenia zależy od prawdopodobieństwa drugiego zdarzenia. Zatem, gdy dwa zdarzenia A i B są zależne, prawdopodobieństwo warunkowe zdarzenia A przy danym zdarzeniu B różni się od prawdopodobieństwa wystąpienia zdarzenia A.

Rozwiązane ćwiczenia z prawdopodobieństwa warunkowego

Ćwiczenie 1

Wiemy, że w worku pełnym piłek połowa jest pomarańczowa, a druga zielona. Dodatkowo jedna trzecia wszystkich piłek jest pomarańczowa i jednocześnie oznaczona znakiem. Jakie jest prawdopodobieństwo, że wylosowana pomarańczowa kula otrzyma sygnał?

Aby rozwiązać zadanie, musimy zastosować wzór na prawdopodobieństwo warunkowy, który wynosi:

Stwierdzenie problemu mówi nam, że połowa worka to pomarańcze. Zatem teoretyczne prawdopodobieństwo podniesienia pomarańczowej kuli wynosi 50%.

Z drugiej strony wiemy, że jedną trzecią całości stanowią kule pomarańczowe i mają sygnał, zatem prawdopodobieństwo otrzymania kulki pomarańczowej z sygnałem wynosi:

Na koniec podstawiamy obliczone prawdopodobieństwa do wzoru na prawdopodobieństwo warunkowe, aby znaleźć jego wartość:

Podsumowując, prawdopodobieństwo wylosowania kuli z sygnałem, jeśli jest pomarańczowa, wynosi 66%.

Ćwiczenie 2

Jeśli w pudełku mamy sześć niebieskich długopisów i trzy czarne długopisy, oblicz prawdopodobieństwo wylosowania jednego niebieskiego długopisu i prawdopodobieństwo wylosowania dwóch niebieskich długopisów pod rząd.

Aby określić prawdopodobieństwo, że raz podniesiesz niebieski długopis, po prostu skorzystaj z prawa Laplace’a:

Zadanie wymaga również poznania prawdopodobieństwa podniesienia kolejno dwóch niebieskich długopisów, czyli warunkowego prawdopodobieństwa podniesienia niebieskiego długopisu, jeśli już wcześniej podnieśliśmy niebieski długopis.

Jeśli narysujemy niebieski długopis, mamy mniej korzystny przypadek, ale w sumie jest też o jeden długopis mniej. Prawdopodobieństwo warunkowe wynosi zatem:

Ćwiczenie 3

Jakie jest prawdopodobieństwo warunkowe wyrzucenia kostki do liczby 4, jeśli w wyniku rzutu monetą wypadną reszki?

Aby rozwiązać to ćwiczenie, należy wziąć pod uwagę teorię prawdopodobieństwa warunkowego, ponieważ zdarzenia „uzyskanie liczby 4 w wyniku rzutu kostką” i „uzyskanie orła w wyniku rzutu monetą” są niezależne. Nie jest zatem konieczne stosowanie wzoru na prawdopodobieństwo warunkowe, ale spełniona jest następująca równość:

Aby znaleźć prawdopodobieństwo warunkowe, po prostu skorzystaj z reguły Laplace’a:

Ćwiczenie 4

Zbadano rok finansowy 25 spółek w danym kraju oraz to, jak zmieniają się ceny ich akcji w zależności od wyniku ekonomicznego roku. Zebrane dane można zobaczyć w poniższej tabeli awaryjnej:

Jakie jest prawdopodobieństwo wzrostu ceny akcji spółki, jeśli osiągnęła ona zysk w ciągu ostatniego roku?

W ćwiczeniu pytamy o warunkowe prawdopodobieństwo wzrostu wartości zapasów przy założeniu, że spółka osiągnęła dodatni wynik ekonomiczny. Aby więc obliczyć to prawdopodobieństwo, musimy skorzystać ze wzoru na prawdopodobieństwo warunkowe:

Dlatego najpierw obliczamy prawdopodobieństwo, że spółka osiągnie zysk, a po drugie, prawdopodobieństwo, że spółka osiągnie zysk ekonomiczny, zwiększając cenę za akcję:

Następnie podstawiamy znalezione wartości do wzoru i obliczamy prawdopodobieństwo warunkowe:

Własności prawdopodobieństwa warunkowego

Właściwości prawdopodobieństwa warunkowego lub prawdopodobieństwa warunkowego są następujące:

• Suma prawdopodobieństwa warunkowego zdarzenia A danego zdarzenia B plus prawdopodobieństwa warunkowego zdarzenia uzupełniającego A danego zdarzenia B jest równa jeden.

• Jeśli zdarzenie A jest podzbiorem zdarzenia B, A zawsze wystąpi, gdy B będzie prawdziwe. Zatem prawdopodobieństwo warunkowe zdarzenia A przy danym zdarzeniu B w tych przypadkach wynosi 1.

• Biorąc pod uwagę dwa różne zdarzenia, zawsze zachodzi następująca równość w odniesieniu do prawdopodobieństwa warunkowego: