Jak obliczyć prawdopodobieństwo wyrzucenia reszki w rzucie monetą
Przy danym rzucie monetą prawdopodobieństwo wyrzucenia orła wynosi 1/2 lub 0,5.
Aby obliczyć prawdopodobieństwo wyrzucenia co najmniej jednego orła w określonej liczbie rzutów monetą, możesz skorzystać z następującego wzoru:
P(Co najmniej jedna głowa) = 1 – 0,5 n
Złoto:
- n : Całkowita liczba odwróceń
Załóżmy na przykład, że rzucamy monetą 2 razy.
Prawdopodobieństwo zdobycia co najmniej jednej reszki podczas tych 3 rzutów wynosi:
- P(Co najmniej jedna głowa) = 1 – 0,5 n
- P(Co najmniej jedna głowa) = 1 – 0,5 3
- P (Co najmniej jedna głowa) = 1 – 0,125
- P(Co najmniej jedna głowa) = 0,875
Ta odpowiedź ma sens, jeśli wyszczególnimy wszystkie możliwe wyniki dwóch rzutów monetą, gdzie „T” oznacza reszkę, a „H” oznacza reszkę:
- TTT
- TTH
- THH
- THT
- HHHH
- VRD
- HTH
- HTT
Należy zauważyć, że co najmniej jedna reszka (H) pojawia się w 7 z 8 możliwych wyników, co równa się 7/8 = 0,875 .
Albo załóżmy, że rzucamy monetą 5 razy.
Prawdopodobieństwo zdobycia co najmniej jednej reszki podczas tych 5 rzutów wynosi:
- P(Co najmniej jedna głowa) = 1 – 0,5 n
- P(Co najmniej jedna głowa) = 1 – 0,5 5
- P(Co najmniej jedna głowa) = 1 – 0,25
- P(Co najmniej jedna głowa) = 0,96875
Poniższa tabela pokazuje prawdopodobieństwo wyrzucenia co najmniej jednego orła przy różnej liczbie rzutów monetą:
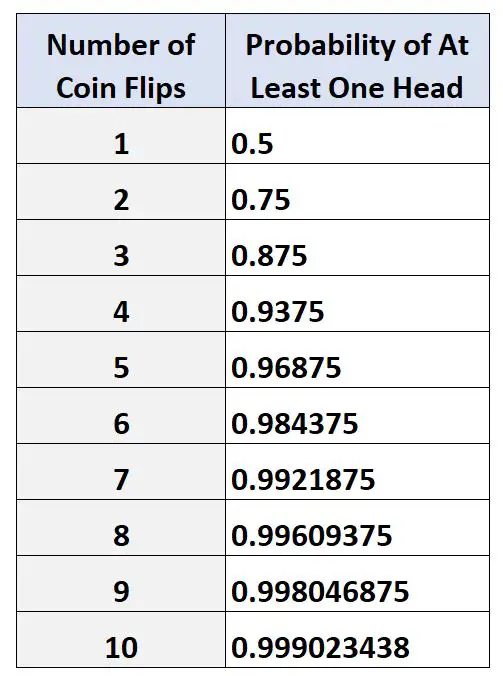
Należy pamiętać, że im większa liczba rzutów monetą, tym większe prawdopodobieństwo wyrzucenia co najmniej jednej reszki.
Powinno to mieć sens, biorąc pod uwagę, że powinniśmy mieć większe prawdopodobieństwo, że w końcu zobaczymy reszkę, jeśli będziemy wielokrotnie rzucać monetą.
Dodatkowe zasoby
Poniższe samouczki wyjaśniają, jak wykonywać inne typowe obliczenia związane z prawdopodobieństwem:
Jak znaleźć prawdopodobieństwo „co najmniej jednego” sukcesu
Jak znaleźć prawdopodobieństwo „co najmniej dwóch” sukcesów
Jak znaleźć prawdopodobieństwo A i B
Jak znaleźć prawdopodobieństwo A lub B