Prawo benforda
W tym artykule wyjaśniono, czym jest prawo Benforda. Dodatkowo będziesz mógł zobaczyć, jak odkryto prawo Benforda i jakie są zastosowania tego prawa statystycznego.
Co to jest prawo Benforda?
Prawo Benforda , zwane także prawem pierwszej cyfry , jest prawem statystycznym, które mówi, że prawdopodobieństwo, że pierwszą cyfrą danej jest 1, jest większe niż prawdopodobieństwo, że jest to inna liczba.
Innymi słowy, prawo Benforda mówi, że w zbiorze danych liczbowych istniejących w prawdziwym życiu liczba 1 jest liczbą najczęściej powtarzaną jako pierwsza cyfra danych.
Ponadto im wyższa liczba, tym mniejsze prawdopodobieństwo, że zajmie pierwsze miejsce. Zatem pierwsza liczba jest bardziej prawdopodobna niż 2, ale 2 jest bardziej prawdopodobne niż 3, 3 jest bardziej prawdopodobne niż 4 i tak dalej.
Prawo Benforda swoją nazwę zawdzięcza Amerykaninowi Frankowi Benfordowi. Chociaż Benford tego nie wymyślił, spopularyzował tę regułę statystyczną. Poniżej zobaczymy pochodzenie prawa Benforda.
Wzór na prawo Benforda
Prawo Benforda stwierdza, że prawdopodobieństwo, że pierwszą cyfrą jest określona liczba, jest równe logarytmowi jeden plus jeden przez tę liczbę.
Wzór na prawo Benforda jest zatem następujący:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle P[X=d]=\log_{10}\left(1+\frac{1}{d}\right)\\[4ex]d=1,2,3,\ldots ,9\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-a77defb5b209293a074ac2bee02c2e07_l3.png)
Dlatego ze wzoru na prawo Benforda możemy dla każdej liczby wyprowadzić prawdopodobieństwo, że jest to pierwsza cyfra elementu danych. W poniższej tabeli możesz zobaczyć procenty wszystkich prawdopodobieństw:
| Postać | Prawdopodobieństwo, że być pierwszą liczbą |
|---|---|
| 1 | 30,1% |
| 2 | 17,6% |
| 3 | 12,5% |
| 4 | 9,7% |
| 5 | 7,9% |
| 6 | 6,7% |
| 7 | 5,8% |
| 8 | 5,1% |
| 9 | 4,6% |
Dodatkowo poniżej możesz zobaczyć histogram, na którym graficznie przedstawiono wszystkie prawdopodobieństwa prawa Benforda:
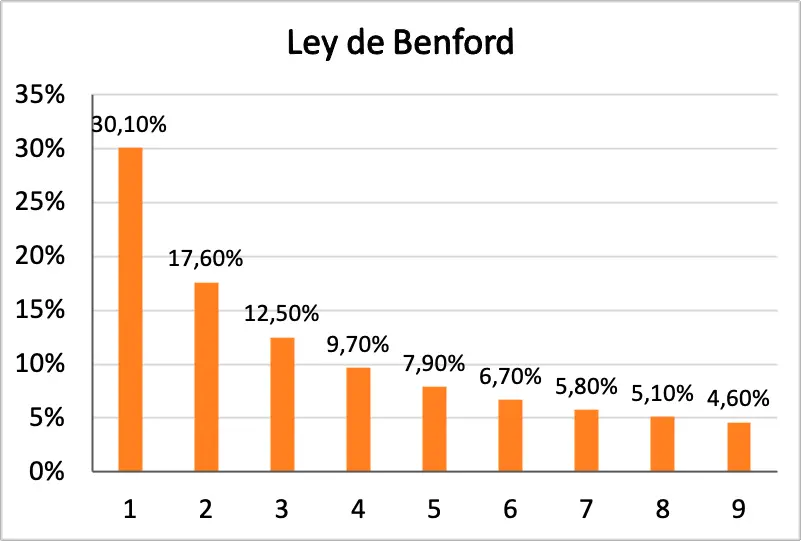
Historia prawa Benforda
W 1881 roku matematyk Simon Newcomb wydedukował prawo Benforda, gdy odkrył, że pierwsze strony tablic logarytmicznych były wykorzystywane znacznie częściej niż ostatnie strony. Oznaczało to, że pierwsze cyfry liczb nie są jednakowo prawdopodobne, ale 1 występowało częściej niż 2, 2 częściej niż 3 i tak dalej, aż do 9.
Jednak Newcomb nie pozostawił żadnych statystycznych dowodów na to, że zasada ta była przestrzegana, po prostu wywnioskował ze zużycia tablic logarytmicznych.
Później, konkretnie w 1938 roku, fizyk Frank Benford dokonał tej samej obserwacji, a także przeprowadził eksperyment, aby zweryfikować ją empirycznie. Na zbiorze danych statystycznych składającym się z 20 229 wartości z 20 różnych próbek przeprowadził badanie pierwszej cyfry każdej z danych. Zatem na podstawie wyników wykazał, że prawo Benforda zostało spełnione i wyprowadził wzór, który pozwolił mu obliczyć prawdopodobieństwo, że pierwsza cyfra będzie określoną liczbą (ten wzór widzieliśmy powyżej).
Krótko mówiąc, chociaż prawo Benforda zostało po raz pierwszy odkryte przez Simona Newcomba, jego imię pochodzi od Franka Benforda, ponieważ to on zweryfikował to prawo statystyczne.
Zastosowania prawa Benforda
Prawo Benforda jest prawem statystycznym, które znajduje zastosowanie w bardzo różnych dziedzinach. Na przykład prawo Benforda jest szeroko stosowane w ekonomii, biologii, a nawet polityce.
W ekonomii prawo Benforda jest często używane do wykrywania manipulacji danymi, ponieważ jeśli zbiór danych nie jest zgodny z prawem Benforda, oznacza to, że dane zostały zmanipulowane. Prawo to wykorzystywane jest m.in. do wykrywania ewentualnych przypadków oszustw podatkowych.
Należy zauważyć, że prawa Benforda nie stosuje się do wykazania prawdziwości zjawisk losowych, ponieważ wyniki są jednakowo prawdopodobne. Zatem reguły Benforda nie można stosować do weryfikacji wyników loterii.
Z drugiej strony w genetyce prawo Benforda można wykorzystać do analizy różnic w długości genomu między różnymi typami organizmów.
Wreszcie podjęto także próby wykrywania oszustw wyborczych poprzez zastosowanie prawa Benforda, chociaż jego przydatność w tym przypadku była kwestionowana.