Rozkład pareto
W tym artykule wyjaśniono, czym jest rozkład Pareto w statystyce i do czego służy. Będziesz także mógł zobaczyć wykres rozkładu Pareto i właściwości tego typu rozkładu prawdopodobieństwa.
Co to jest dystrybucja Pareto?
Rozkład Pareto to ciągły rozkład prawdopodobieństwa stosowany w statystyce do modelowania zasady Pareto. Zatem rozkład Pareto jest rozkładem prawdopodobieństwa, który ma kilka wartości, których prawdopodobieństwo wystąpienia jest znacznie większe niż pozostałych wartości.
Pamiętaj, że prawo Pareto, zwane także zasadą 80-20, jest zasadą statystyczną, która mówi, że za większość przyczyn zjawiska odpowiada niewielka część populacji.
Rozkład Pareto ma dwa charakterystyczne parametry: parametr skali x m i parametr kształtu α.
![]()
Pierwotnie rozkład Pareto był używany do opisania rozkładu bogactwa w populacji, ponieważ większość z niego wynikała z małej części populacji. Ale obecnie rozkład Pareto ma wiele zastosowań, na przykład w kontroli jakości, w ekonomii, w nauce, w obszarze społecznym itp.
Rozkład Pareto został nazwany na cześć ekonomisty Vilfredo Pareto, który go sformułował. Jednak najbardziej znany jest z wykresu Pareto.
Tabela rozkładu Pareto
Teraz, gdy znamy definicję rozkładu Pareto, spójrzmy na kilka przykładów rozkładów Pareto przedstawionych graficznie.
Poniżej możesz więc zobaczyć jak wygląda wykres funkcji gęstości rozkładu Pareto w zależności od jej charakterystycznych wartości:
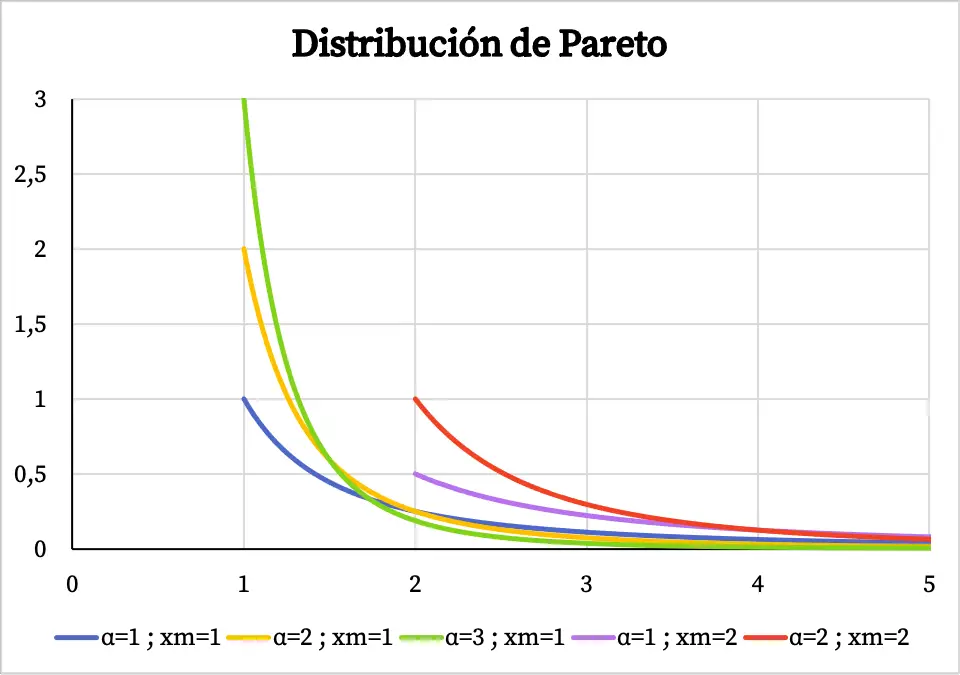
Należy zauważyć, że dziedzina rozkładu Pareto rozciąga się od wartości x m do +∞, dlatego funkcja gęstości nie istnieje przed wartością x m .
Natomiast wykres skumulowanej funkcji prawdopodobieństwa rozkładu Pareto wygląda następująco:
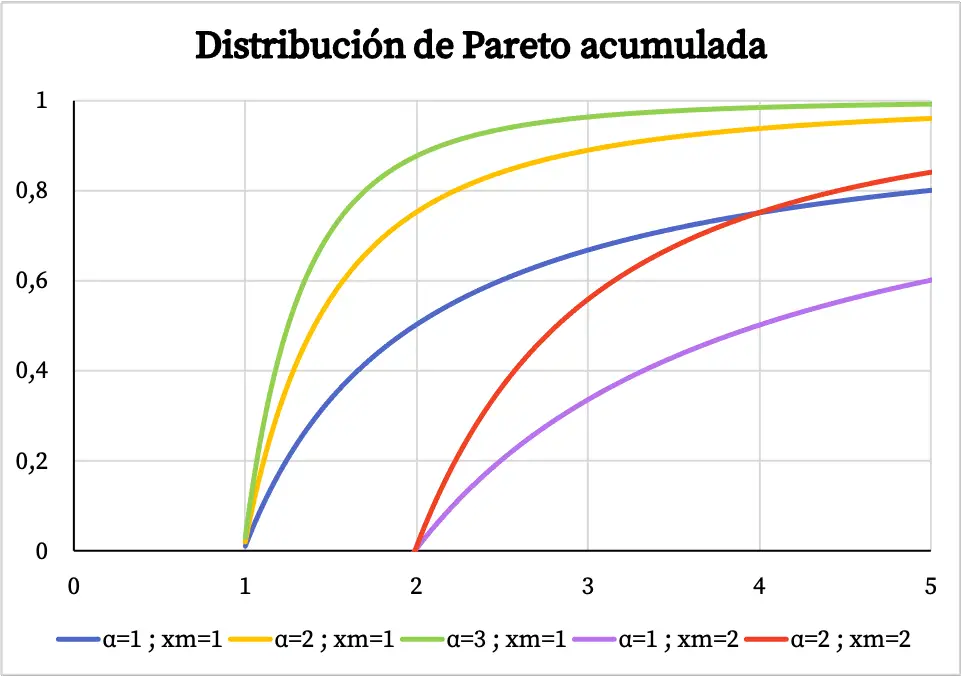
Charakterystyka rozkładu Pareto
Poniżej przedstawiono najważniejsze cechy rozkładu Pareto związane z teorią prawdopodobieństwa i statystyką.
- Rozkład Pareto ma dwa charakterystyczne parametry określające jego krzywą: parametr skali x m i parametr kształtu α.
![]()
- Dziedzina rozkładu Pareto składa się ze wszystkich liczb rzeczywistych od parametru skali do plus nieskończoności.
![]()
- Jeśli α jest większe niż 1, średnia rozkładu Pareto jest równa iloczynowi α razy x m i α minus 1.
![E[X]=\cfrac{\alpha\cdot x_m}{\alpha-1}\quad\text{para } \alpha>1″ title=”Rendered by QuickLaTeX.com” height=”34″ width=”214″ style=”vertical-align: -12px;”></p>
</p>
<ul>
<li> Wariancja rozkładu Pareto zależy od dwóch charakterystycznych parametrów rozkładu i jest obliczana ze wzoru:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-6d26513868f9ed6fa45ab0fde0030884_l3.png)
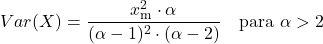
![]()
- Tryb rozkładu Pareto jest równoważny parametrowi skali x m rozkładu.
![]()
- Wzór na funkcję gęstości rozkładu Pareto to:
![]()
- Podobnie wzór na skumulowaną funkcję prawdopodobieństwa rozkładu Pareto wygląda następująco:
![]()
- Współczynnik asymetrii rozkładu Pareto zależy wyłącznie od parametru kształtu α i jego wyrazem jest:
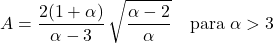
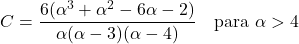
o autorze
Dr Benjamin Anderson
Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej