Jak wykonać test white'a w sas-ie
Test White’a służy do określenia, czy w modelu regresji występuje heteroskedastyczność .
Heteroscedastyczność odnosi się do nierównomiernego rozproszenia reszt na różnych poziomachzmiennej odpowiedzi w modelu regresji, co narusza jedno z kluczowych założeń regresji liniowej , że reszty są równomiernie rozproszone na każdym poziomie zmiennej odpowiedzi.
W tym samouczku wyjaśniono, jak wykonać test White’a w SAS-ie, aby określić, czy heteroskedastyczność jest problemem w danym modelu regresji.
Przykład: test bieli w SAS-ie
Załóżmy, że chcemy dopasować model regresji liniowej wielokrotnej, który wykorzystuje liczbę godzin spędzonych na nauce i liczbę zdanych egzaminów praktycznych, aby przewidzieć końcową ocenę uczniów z egzaminu:
Wynik egzaminu = β 0 + β 1 (godziny) + β 2 (egzaminy przygotowawcze)
Najpierw użyjemy następującego kodu, aby utworzyć zbiór danych zawierający te informacje dla 20 uczniów:
/*create dataset*/ data exam_data; input hours prep_exams score; datalines ; 1 1 76 2 3 78 2 3 85 4 5 88 2 2 72 1 2 69 5 1 94 4 1 94 2 0 88 4 3 92 4 4 90 3 3 75 6 2 90 5 4 90 3 4 82 4 4 85 6 5 90 2 1 83 1 0 62 2 1 76 ; run ; /*view dataset*/ proc print data =exam_data;
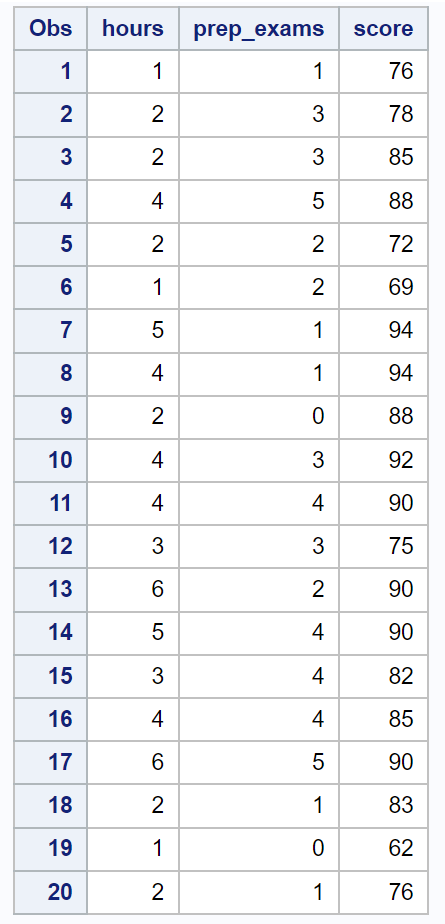
Następnie użyjemy proc reg, aby dopasować ten model regresji liniowej, a także opcji spec , aby wykonać test White’a na heteroskedastyczność:
/*fit regression model and perform White's test*/
proc reg data =exam_data;
model score = hours prep_exams / spec ;
run ;
quit ;
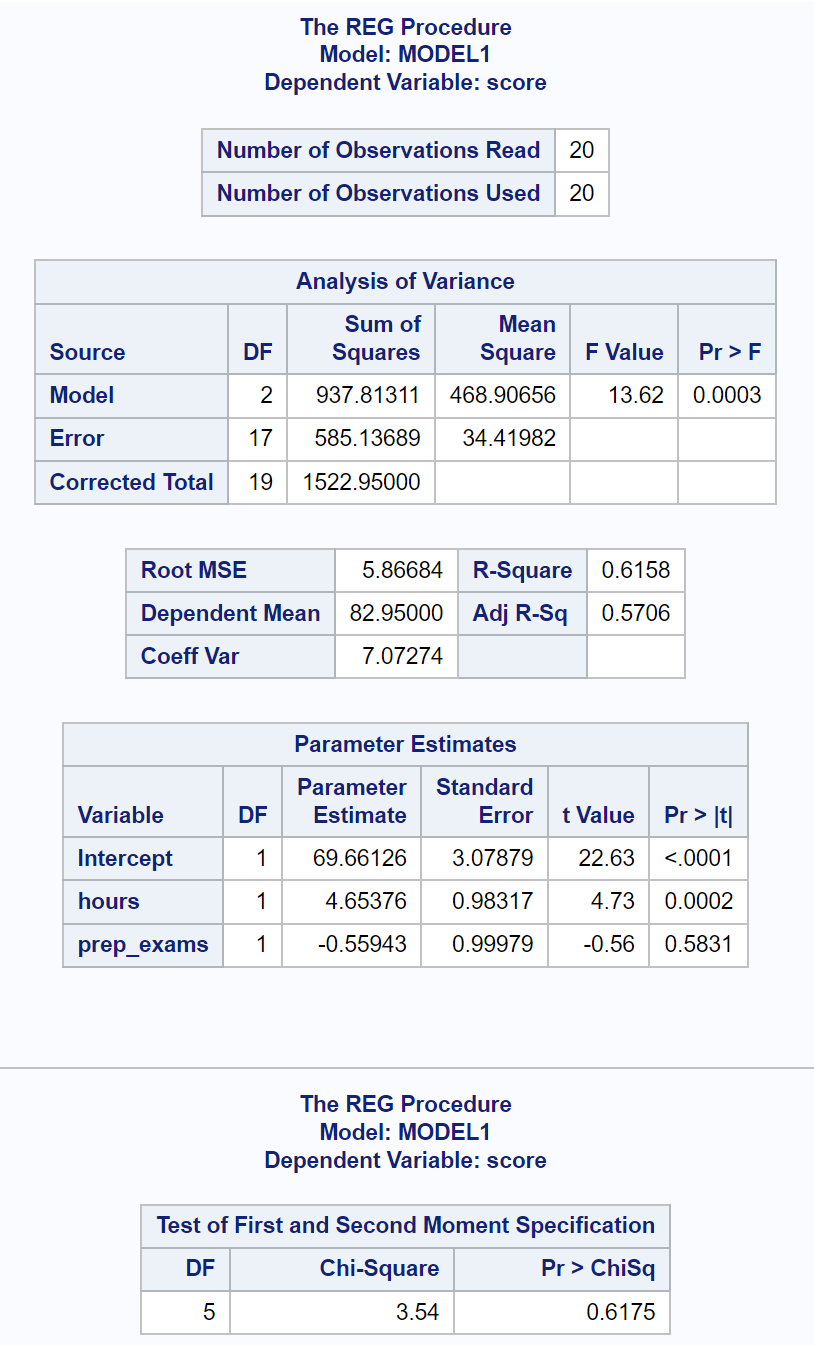
Ostatnia tabela wyników przedstawia wyniki testu White’a.
Z tej tabeli widzimy, że statystyka testu Chi-kwadrat wynosi 3,54 , a odpowiadająca jej wartość p wynosi 0,6175 .
W teście White’a wykorzystuje się następujące hipotezy zerowe i alternatywne:
- Null (H 0 ) : Heteroskedastyczność nie występuje.
- Alternatywa ( HA ): Występuje heteroskedastyczność.
Ponieważ wartość p jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej.
Oznacza to, że nie mamy wystarczających dowodów, aby twierdzić, że w modelu regresji występuje heteroskedastyczność.
Można zatem bezpiecznie interpretować błędy standardowe oszacowań współczynników w tabeli podsumowującej regresję.
Co zrobic nastepnie
Jeśli nie odrzucisz hipotezy zerowej testu White’a, oznacza to, że heteroskedastyczność nie występuje i możesz przystąpić do interpretacji wyniku pierwotnej regresji.
Jeśli jednak odrzucisz hipotezę zerową, oznacza to, że w danych występuje heteroskedastyczność. W takim przypadku błędy standardowe wyświetlane w tabeli wyników regresji mogą być niewiarygodne.
Istnieje kilka typowych sposobów rozwiązania tego problemu, w tym:
1. Przekształć zmienną odpowiedzi. Możesz spróbować przeprowadzić transformację zmiennej odpowiedzi.
Można na przykład użyć zmiennej odpowiedzi dziennika zamiast oryginalnej zmiennej odpowiedzi.
Ogólnie rzecz biorąc , skutecznym sposobem na wyeliminowanie heteroskedastyczności jest obliczenie logu zmiennej odpowiedzi.
Inną powszechną transformacją jest użycie pierwiastka kwadratowego ze zmiennej odpowiedzi.
2. Zastosuj regresję ważoną. Ten typ regresji przypisuje wagę każdemu punktowi danych na podstawie wariancji jego dopasowanej wartości.
Daje to małe wagi punktom danych o większych wariancjach, redukując ich kwadraty resztowe.
Zastosowanie odpowiednich wag może wyeliminować problem heteroskedastyczności.