Jak wykonać test t dla jednej próby w sas

Test t dla jednej próby służy do określenia, czy średnia populacji jest równa określonej wartości.

W tym samouczku wyjaśniono, jak wykonać test t dla jednej próby w SAS-ie.

Przykład: przykładowy test t w SAS

Załóżmy, że botanik chce wiedzieć, czy średnia wysokość określonego gatunku rośliny wynosi 15 cali. Bierze losową próbkę 12 roślin i zapisuje wysokość każdej z nich w calach.

Wysokości to: 14, 14, 16, 13, 12, 17, 15, 14, 15, 13, 15, 14

Wykonaj poniższe kroki, aby przeprowadzić test t dla jednej próbki i ustalić, czy średnia wysokość tego gatunku roślin wynosi w rzeczywistości 15 cali.

Krok 1: Utwórz dane.

Najpierw użyjemy poniższego kodu do utworzenia zbioru danych w SAS-ie:

 /*create dataset*/
data my_data;
    inputHeight ;
    datalines ;
14
14
16
13
12
17
15
14
15
13
15
14
;
run ;

/*print dataset*/
proc print data =my_data; 

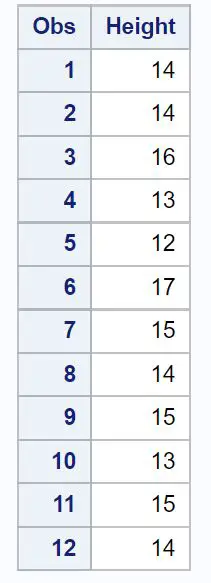
Krok 2: Wykonaj test t dla jednej próbki.

Następnie użyjemy proc ttest do wykonania testu t na przykładzie:

 /*perform one sample t-test*/
proc ttest data =my_data sides = 2 alpha = 0.05 h0 = 15 ;
    varHeight ;
run ;

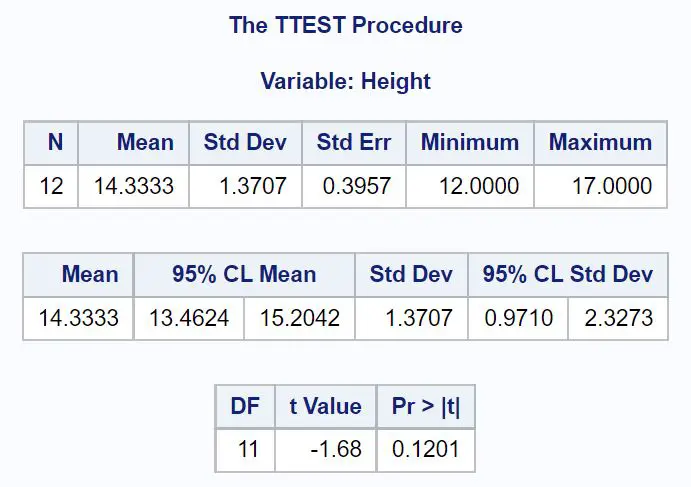
Pierwsza tabela przedstawia statystyki opisowe dla naszej próby, w tym:

• N (obserwacje ogółem): 12
• Średnia (średnia próbki): 14,3333
• Std Dev (odchylenie standardowe próbki): 1,3707
• Błąd standardowy (błąd standardowy, obliczany jako s/ √n ): 0,3957
• Minimum (wartość minimalna): 12
• Maksimum (wartość maksymalna) 17

Druga tabela przedstawia 95% przedział ufności dla prawdziwej średniej populacji:

• 95% CI dla μ: [13,4624, 15,2042]

Trzecia tabela przedstawia statystykę testu t i odpowiadającą jej wartość p:

• Statystyka testu t: -1,68
• Wartość p: 0,1201

Uwaga : Statystykę testową obliczono w następujący sposób:

• t statystyka testowa = ( x – μ) / (s/ √n )
• Statystyka testu t = (14,3333-15) / (1,3707/√ 12 )
• statystyka testu t = -1,68

Przypomnijmy, że test t dla jednej próby wykorzystuje następujące hipotezy zerowe i alternatywne:

• H ₀ : μ = 15 cali
• H _A : μ ≠ 15 cali

Ponieważ wartość p ( 0,1201 ) jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej.

Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że średnia wysokość niektórych gatunków roślin różni się od 15 cali.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne popularne testy statystyczne w SAS-ie:

Jak wykonać test rangowy ze znakiem Wilcoxona w SAS
Jak wykonać jednokierunkową ANOVA w SAS