Próbkowanie warstwowe
W tym artykule wyjaśniamy, czym jest próbkowanie warstwowe i w jaki sposób jest przeprowadzane. Tutaj znajdziesz wyjaśnienie podtypów próbkowania warstwowego i wreszcie, jakie są zalety i wady próbkowania warstwowego.
Co to jest próbkowanie warstwowe?
Dobór warstwowy to metoda statystyczna stosowana do doboru elementów próby poprzez podzielenie populacji na grupy (zwane warstwami). Oznacza to, że w próbkowaniu warstwowym populację dzieli się na warstwy, a osoby z każdej warstwy są wybierane losowo w celu utworzenia całej próby badawczej.
Warstwy to jednorodne grupy, czyli innymi słowy jednostki w danej warstwie mają swoje własne cechy, które odróżniają je od innych warstw. Jednostka może zatem należeć tylko do jednej warstwy.
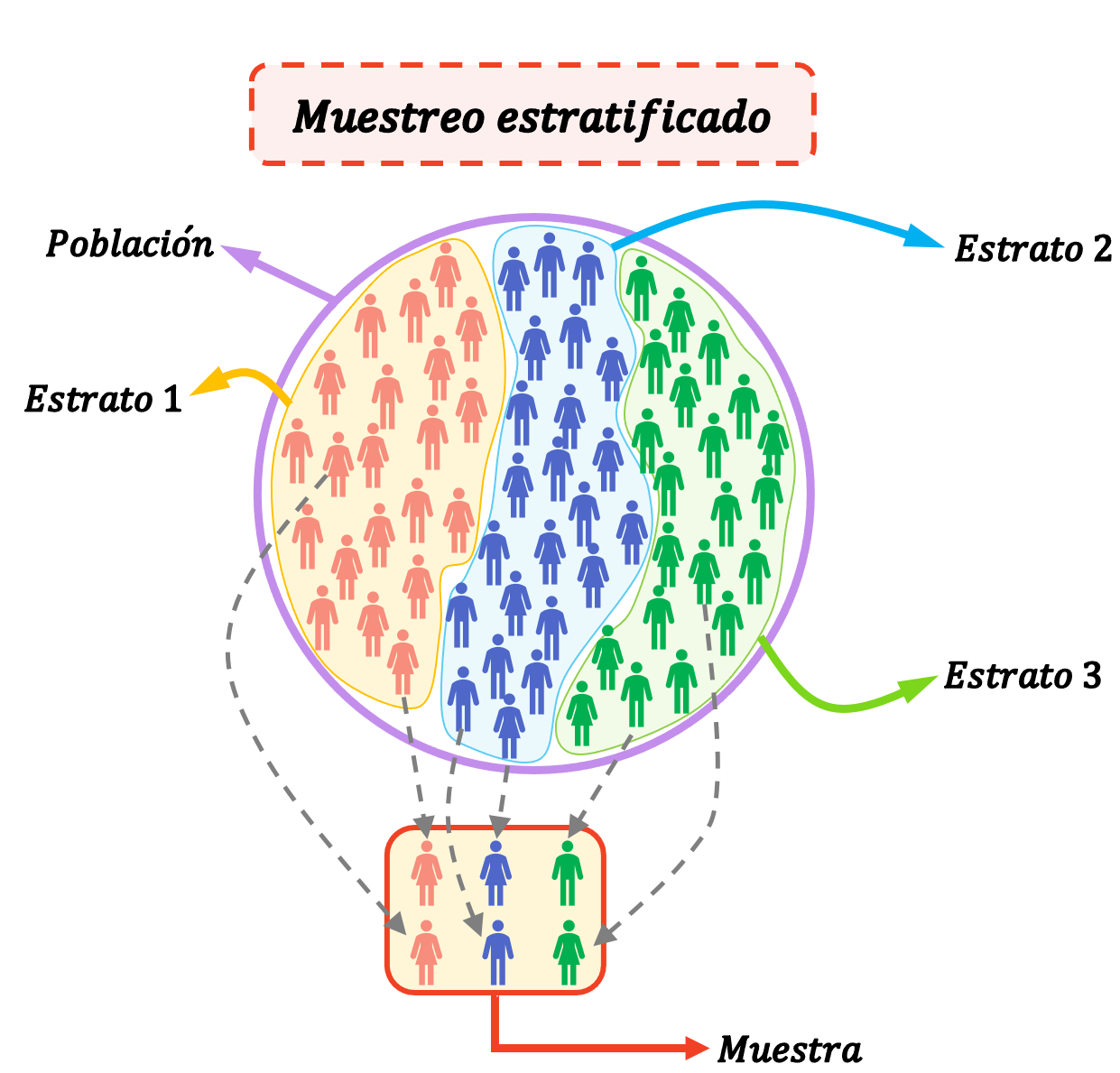
Dobór warstwowy jest bardzo przydatny, gdy populacja składa się z bardzo jednorodnych grup, które bardzo się od siebie różnią.
Logicznie rzecz biorąc, suma wielkości wszystkich warstw daje wielkość populacji statystycznej:
![]()
Podobnie suma wielkości próby wybranej w każdej warstwie jest równa całkowitej wielkości próby w badaniu statystycznym:
![]()
Generalnie rozróżniamy wielkie i małe litery, aby oznaczyć odpowiednio populację lub próbkę.
Jak przeprowadzić próbkowanie warstwowe
Etapy przeprowadzania próbkowania warstwowego są następujące:
- Zdefiniuj populację docelową.
- Wybierz zmienną stratyfikację i liczbę warstw.
- Określ , do której warstwy należy każdy element populacji.
- Oblicz wielkość każdej warstwy , która będzie częścią próbki.
- Należy losowo wybrać elementy z każdej warstwy , które będą należeć do próby badawczej. Dla każdej warstwy należy wybrać tyle elementów, ile ustalono w poprzednim kroku.
Należy pamiętać, że wielkość każdej warstwy w próbie zależy nie tylko od wielkości warstwy, ale także od rodzaju warstwowego próbkowania. Następnie na przykładzie wyjaśniono każdy rodzaj doboru warstwowego oraz sposób obliczania wielkości próby w każdej warstwie.
Rodzaje próbkowania warstwowego
Teraz, gdy znasz już definicję próbkowania warstwowego, powinieneś wiedzieć, że istnieje kilka rodzajów próbkowania warstwowego, które są sklasyfikowane w następujący sposób:
- Proporcjonalne próbkowanie warstwowe
- Jednolite próbkowanie warstwowe
- Próbkowanie jest optymalne
Każdy rodzaj próbkowania warstwowego został szczegółowo wyjaśniony poniżej, aby lepiej zrozumieć znaczenie każdego z nich.
Proporcjonalne próbkowanie warstwowe
W warstwowym doborze proporcjonalnym lub proporcjonalnym doborze alokacyjnym liczba elementów z każdej warstwy wchodzących w skład próby badawczej jest proporcjonalna do wielkości każdej warstwy.
Zatem jeśli jedna warstwa jest większa od drugiej, ostateczna próbka będzie zawierać więcej elementów z tej warstwy. Z drugiej strony, jeśli jedna warstwa jest mniejsza od drugiej, w próbie do analizy statystycznej będzie mniej elementów z tej warstwy.
Ten rodzaj próbkowania warstwowego jest przydatny, gdy warstwy mają różną wielkość i chcemy, aby próbka zawierała więcej elementów z większych warstw.
Aby obliczyć liczbę elementów z każdej warstwy , które znajdą się w próbie, wielkość każdej warstwy należy podzielić przez sumę rozmiarów wszystkich warstw. Wynikiem będzie proporcja warstwy, która powinna zostać uwzględniona w próbie, dlatego należy ją pomnożyć przez pożądaną wielkość próby.
![]()
Złoto
![]()
to całkowity pożądany rozmiar próbki,
![]()
liczba elementów w warstwie
![]()
do włączenia do próby,
![]()
wielkość warstwy
![]()
, I
![]()
całkowita liczba elementów w populacji.
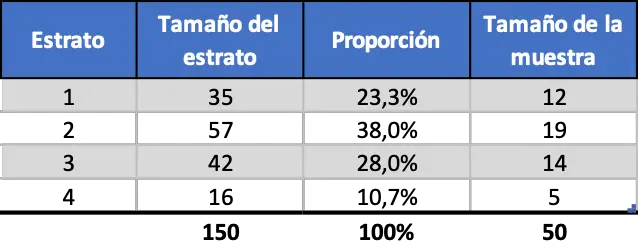
Wyobraźmy sobie na przykład, że chcemy przeprowadzić badanie w firmie zatrudniającej 150 pracowników, biorąc próbę 50 osób i stratyfikując dane w oparciu o wiek pracowników. Dane możemy klasyfikować w następujący sposób:
- Od 20 do 29 lat: 35 pracowników
- Od 30 do 39 lat: 57 pracowników
- Od 40 do 49 lat: 42 pracowników
- Od 50 do 59 lat: 16 pracowników
Zatem, jeśli stratyfikujemy dane proporcjonalnie, próbkowanie będzie wyglądało następująco:
Jednolite próbkowanie warstwowe
W jednolitym próbkowaniu warstwowym lub jednolitym próbkowaniu afiksacyjnym liczba elementów z każdej warstwy wchodzących w skład próby badawczej jest równa.
Każda warstwa ma zatem taką samą wagę w tego rodzaju próbkowaniu. Niezależnie od tego, czy dana warstwa ma więcej czy mniej osobników niż inna warstwa, wszystkie będą reprezentowane w próbie przez tę samą liczbę osobników.
W takim przypadku, aby obliczyć wielkość elementów w każdej warstwie, pożądaną wielkość próby należy podzielić przez liczbę istniejących warstw. Inaczej mówiąc, należy zastosować następujący wzór:
![]()
Złoto
![]()
to całkowity pożądany rozmiar próbki,
![]()
liczba elementów w warstwie
![]()
kto zostanie włączony do próby oraz
![]()
liczba warstw, na które podzielona została populacja.
Idąc za poprzednim przykładem, ponieważ chcieliśmy próby składającej się z 50 pracowników, a w sumie były 4 różne warstwy, wielkość próby każdej warstwy będzie wynosić:
![]()
Wynikiem jest liczba dziesiętna, niektóre warstwy będą miały 12 pracowników, a inne 13, aż do osiągnięcia 50 pracowników. Zatem jednolite pobieranie warstwowe wygląda następująco:
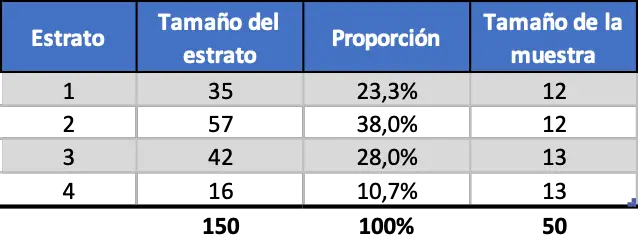
Jak widać, wielkość próby każdej warstwy jest niezależna od proporcji każdej warstwy.
Optymalne próbkowanie warstwowe
W optymalnym próbkowaniu warstwowym liczba elementów w każdej warstwie zależy proporcjonalnie od zmienności każdej warstwy.
Zatem warstwy o większej zmienności będą miały większą liczebność próby i odwrotnie, warstwy o mniejszej zmienności będą miały mniejszą liczebność próby.
Wzór na określenie, ile elementów z każdej warstwy będzie wchodzić w skład próby statystycznej, jest następujący:
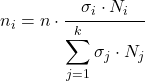
Złoto
![]()
to całkowity pożądany rozmiar próbki,
![]()
to liczba elementów w warstwie
![]()
do włączenia do próby,
![]()
jest odchyleniem standardowym (lub odchyleniem typowym) warstwy
![]()
, I
![]()
to wielkość warstwy
![]()
.
Zalety i wady próbkowania warstwowego
Próbkowanie warstwowe ma następujące zalety i wady:
| korzyść | Niedogodności |
|---|---|
| Umożliwia statystyczne badanie nie tylko całej populacji, ale także poszczególnych jej warstw. | Jest to skomplikowana metoda pobierania próbek do wdrożenia. |
| Błąd próbkowania popełniany w przypadku próbkowania warstwowego jest zawsze równy lub mniejszy niż w przypadku prostego losowania. | Jest to czasochłonny, a przez to kosztowny proces pobierania próbek. |
| Pozwala wykorzystać wiedzę badacza na temat populacji. | Aby dokonać stratyfikacji badanej próby, potrzeba wielu informacji. |
| Przy próbkowaniu warstwowym zapewniamy, że w próbie znajdzie się co najmniej jeden element z każdej warstwy. | Aby móc przeprowadzić pobieranie próbek, konieczna jest znajomość proporcji każdej warstwy. |
Główną cechą doboru warstwowego jest to, że służy on do statystycznej analizy każdej grupy lub warstwy, na którą podzielono populację. Oczywiście za pomocą tego rodzaju próbkowania można badać także całą populację. Ponadto korzyści wynikające ze stratyfikacji danych będą większe, jeśli warstwy będą się od siebie różnić.
Wręcz przeciwnie, fakt stratyfikacji danych w celu umożliwienia przeprowadzenia pobierania próbek oznacza wzrost złożoności pobierania próbek, ponieważ pobieranie próbek warstwowych jest bardziej skomplikowane w porównaniu z innymi rodzajami pobierania próbek. Właściwość ta oznacza również, że wykonanie próbki jest kosztowne, ponieważ prawidłowe przeprowadzenie stratyfikacji wymaga czasu.
Inną wadą doboru warstwowego jest to, że wymaga dużej ilości informacji na temat populacji, którą chcemy zbadać, co nie jest konieczne w przypadku innych rodzajów doboru próby, takich jak proste dobieranie losowe. Chociaż tę wadę można złagodzić, jeśli badacz ma dużą wiedzę w tej dziedzinie.
Wreszcie, przy próbkowaniu warstwowym uzyskujemy próbę, która jest bardziej reprezentatywna dla populacji niż w przypadku innych rodzajów próbkowania, ponieważ zapewniamy uwzględnienie elementów z każdej warstwy. Natomiast w innych próbkach uzyskana próbka nie może zawierać elementów z żadnej warstwy.