Problem monty'ego halla: proste wyjaśnienie wizualne

W starym teleturnieju zatytułowanym Let’s Make a Deal gospodarz Monty Hall przedstawił uczestnikom troje drzwi.

Na jednych drzwiach znajdowała się nagroda, na pozostałych dwóch nie.

Monty prosił uczestnika o wybranie, które drzwi jego zdaniem zawierają nagrodę.

Gdy uczestnik wybrał drzwi, Monty otwierał drzwi, które nie zawierały nagrody.

Nagroda pozostała w jednych z dwojga zamkniętych drzwi.

Następnie Monty pytał kandydata, czy chce zmienić drzwi.

Choć może się to wydawać trudne do uwierzenia, okazuje się, że zmiana drzwi na tym etapie gry tak naprawdę daje większą szansę na wygraną.

Czytaj dalej, aby dowiedzieć się dlaczego!

Problem Monty’ego Halla wyjaśniony wizualnie

Aby zilustrować, dlaczego zmiana drzwi daje większe prawdopodobieństwo wygranej, rozważ następujące scenariusze, w których najpierw wybierasz drzwi 1.

Scenariusz 1: Wybierasz drzwi 1, a nagroda faktycznie znajduje się za drzwiami 1.

W tym przypadku Monty otworzy drzwi 2 lub 3 i pokaże, że za żadnymi z nich nic nie ma. Jeśli pozostaniesz przy drzwiach nr 1, wygrywasz .

Scenariusz 2: Wybierasz drzwi 1, a nagroda faktycznie znajduje się za drzwiami 2.

W tym przypadku Monty musi otworzyć drzwi nr 3 i pokazać, że nic się za nimi nie kryje. Jeśli pozostaniesz przy drzwiach nr 1, przegrywasz .

Scenariusz 3: Wybierasz drzwi 1, a nagroda faktycznie znajduje się za drzwiami 3.

W tym przypadku Monty musi otworzyć drzwi nr 2 i pokazać, że nic się za nimi nie kryje. Jeśli pozostaniesz przy drzwiach nr 1, przegrywasz .

Oto wszystkie możliwe wyniki, jeśli wybierzesz drzwi 1. Pamiętaj, że jeśli pozostaniesz przy drzwiach 1, zaoszczędzisz tylko jedną trzecią czasu. Ale jeśli zmienisz, zaoszczędzisz dwie trzecie czasu.

Poniższa tabela podsumowuje wszystkie możliwe scenariusze w tym teleturnieju, a także wyniki związane z utrzymaniem i zmianami:

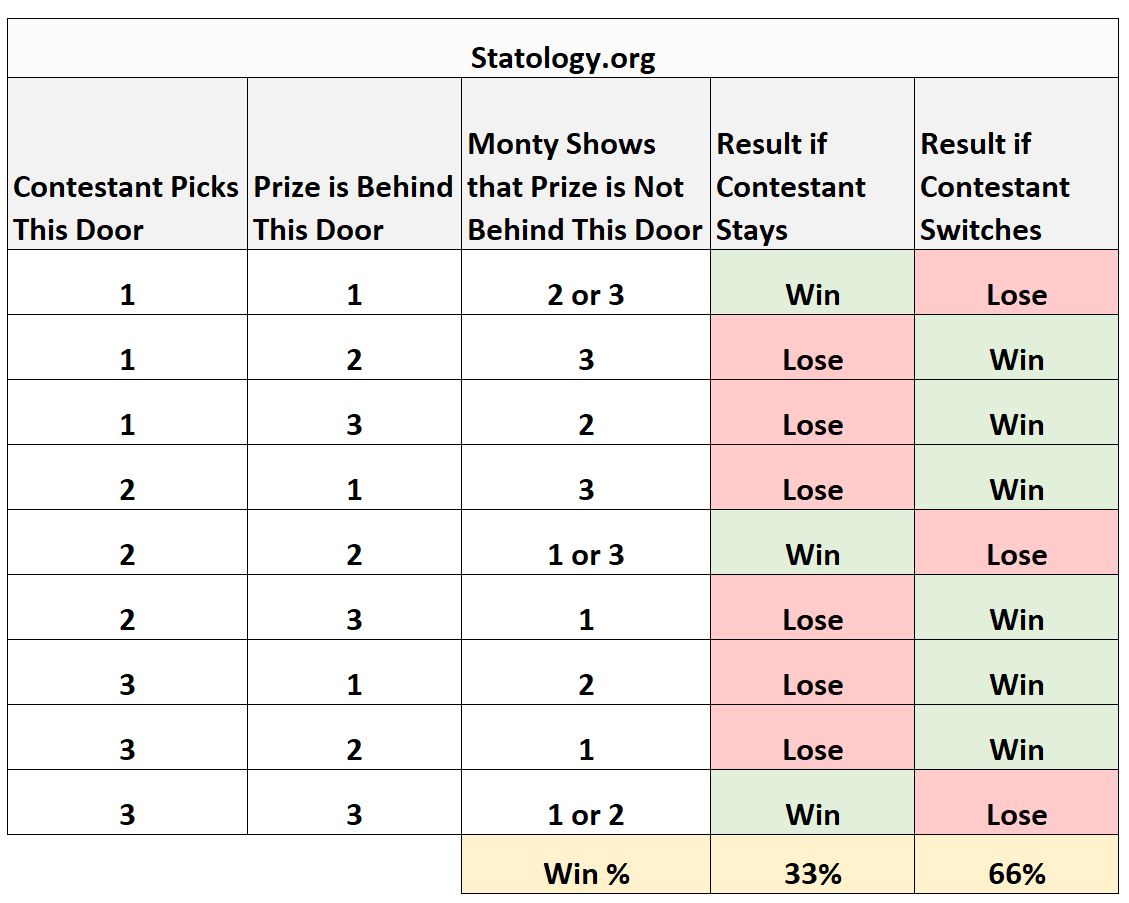
Z tabeli widzimy, że wygrywasz w 33% przypadków, gdy zostajesz, ale wygrywasz w 66% przypadków, gdy zmieniasz firmę.

Zatem zmiana drzwi zwiększa prawdopodobieństwo wygrania nagrody.

Chociaż intuicyjnie może się to wydawać nie mieć sensu, matematyka nie kłamie.