Kompletny przewodnik: projekt czynnikowy 2×4

Projekt czynnikowy 2 × 4 to rodzaj projektu eksperymentalnego, który pozwala badaczom zrozumieć wpływ dwóch zmiennych niezależnych na pojedynczą zmienną zależną.

W tego typu projekcie jedna zmienna niezależna ma dwa poziomy , a druga zmienna niezależna cztery poziomy.

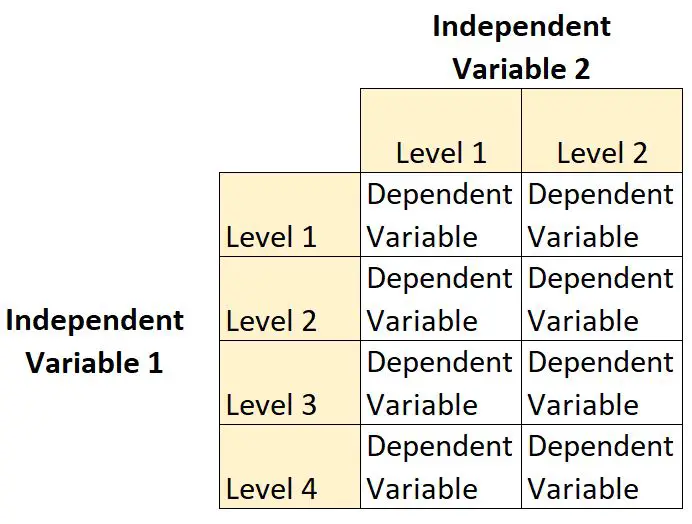
Załóżmy na przykład, że botanik chce zrozumieć wpływ światła słonecznego (brak, niskie, średnie lub wysokie) i częstotliwości podlewania (codziennie lub co tydzień) na wzrost określonego gatunku roślin.

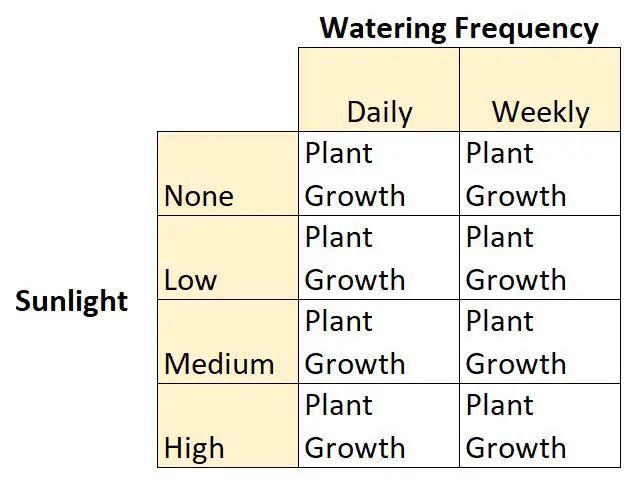
To jest przykład planu czynnikowego 2 × 4, ponieważ istnieją dwie zmienne niezależne, jedna z dwoma poziomami i jedna z czterema poziomami:

• Zmienna niezależna nr 1: Światło słoneczne
  • Poziomy: Brak, Niski, Średni, Wysoki
• Zmienna niezależna nr 2: Częstotliwość podlewania
  • Poziomy: dzienny, tygodniowy

Istnieje również zmienna zależna: wzrost roślin.

Cel projektu czynnikowego 2 × 4

Plan czynnikowy 2×4 umożliwia analizę następujących efektów:

Efekty główne: Są to skutki, jakie pojedyncza zmienna niezależna wywiera na zmienną zależną.

Na przykład w naszym poprzednim scenariuszu mogliśmy przeanalizować następujące efekty główne:

• Główny wpływ światła słonecznego na wzrost roślin.
  • Średni wzrost wszystkich roślin, które nie otrzymały światła słonecznego.
  • Średni wzrost wszystkich roślin o niskim nasłonecznieniu.
  • Średni wzrost wszystkich roślin, które otrzymały średnie nasłonecznienie.
  • Średni wzrost wszystkich roślin, które otrzymały duże nasłonecznienie.
• Główny wpływ częstotliwości podlewania na wzrost roślin.
  • Średni wzrost wszystkich roślin podlewanych codziennie.
  • Średni wzrost wszystkich roślin podlewanych w każdym tygodniu.

Efekty interakcji: Występują, gdy wpływ jednej zmiennej niezależnej na zmienną zależną zależy od poziomu drugiej zmiennej niezależnej.

Na przykład w naszym poprzednim scenariuszu mogliśmy przeanalizować następujące efekty interakcji:

• Czy wpływ nasłonecznienia na wzrost roślin zależy od częstotliwości podlewania?
• Czy wpływ częstotliwości podlewania na wzrost roślin zależy od nasłonecznienia?

Jak analizować projekt czynnikowy 2 × 4

Możemy przeprowadzić dwuczynnikową analizę ANOVA , aby formalnie sprawdzić, czy zmienne niezależne mają statystycznie istotny związek ze zmienną zależną.

Na przykład poniższy kod pokazuje, jak przeprowadzić dwukierunkową analizę ANOVA dla naszego hipotetycznego scenariusza fabryki w R:

 #make this example reproducible
set. seeds (0)

#createdata
df <- data. frame (sunlight = rep(c(' None ', ' Low ', ' Medium ', ' High '), each= 10 , times= 2 ),
                 water = rep(c(' Daily ', ' Weekly '), each= 40 , times= 2 ),
                 growth = c(rnorm(10, 8, 2), rnorm(10, 8, 3), rnorm(10, 13, 2),
                            rnorm(10, 14, 3), rnorm(10, 10, 4), rnorm(10, 12, 3),
                            rnorm(10, 13, 2), rnorm(10, 14, 4)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

                Df Sum Sq Mean Sq F value Pr(>F)    
sunlight 3 744.1 248.04 34.16 < 2e-16 ***
water 1 43.1 43.05 5.93 0.016 *  
sunlight:water 3 195.8 65.27 8.99 1.61e-05 ***
Residuals 152 1103.5 7.26                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Oto jak interpretować wynik ANOVA:

Efekt główny nr 1 (światło słoneczne) : Wartość p związana ze światłem słonecznym wynosi <2e-16 . Ponieważ liczba ta jest mniejsza niż 0,05, oznacza to, że ekspozycja na światło słoneczne ma statystycznie istotny wpływ na wzrost roślin.

Efekt główny nr 2 (Woda) : Wartość p związana z wodą wynosi 0,016 . Ponieważ liczba ta jest mniejsza niż 0,05, oznacza to, że częstotliwość podlewania ma również statystycznie istotny wpływ na wzrost roślin.

Efekt interakcji : Wartość p dla interakcji światła słonecznego i wody wynosi 0,000061 . Ponieważ wartość ta jest mniejsza niż 0,05, oznacza to, że istnieje efekt interakcji pomiędzy światłem słonecznym i wodą.

Dodatkowe zasoby

Poniższe samouczki dostarczają dodatkowych informacji na temat projektowania i analizy eksperymentów:

Kompletny przewodnik: projekt czynnikowy 2 × 2
Kompletny przewodnik: projekt czynnikowy 2 × 3
Co to jest silnia ANOVA?